Энергия вращения двухатомной молекулы в приближении жесткого ротатора. Вращательные спектры молекул и их применение для определения молекулярных характеристик
Появление вращательных спектров связано с тем, что вращательная энергия молекулы квантуется, т.е.
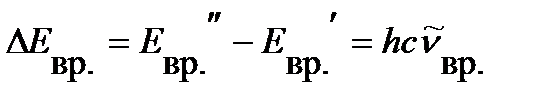 , ,
| (4.26) |
где 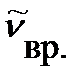 - волновое число линии во вращательном спектре.
- волновое число линии во вращательном спектре.
Рассмотрим механизм возникновения вращательного спектра двухатомной молекулы, межъядерное расстояние в которой постоянно. Такая система называется жестким ротатором.
| m1 |
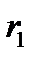
|
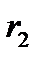
|
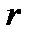
|
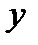
|
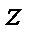
|
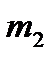
|
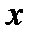
|
| 0 |
| а |
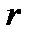
|
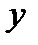
|
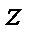
|
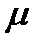
|
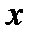
|
| 0 |
| б |
Рисунок 4.4 – Модель жесткого ротатора
на примере двухатомной молекулы (а) и частицы (б)
|
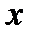
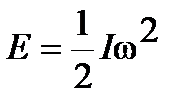 , ,
| (4.27) |
где  - угловая скорость вращения;
- угловая скорость вращения; 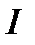 - момент инерции системы:
- момент инерции системы:
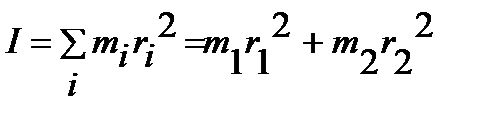 . .
| (4.28) |
Поскольку точка O является центром тяжести молекулы, то:
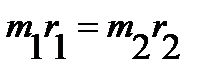 . .
| (4.29) |
Учитывая, что
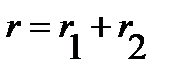
| (4.30) |
равенство (4.29) можно переписать относительно 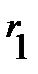 или
или 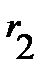 :
:
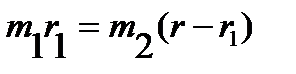 , , 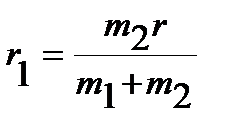 , ,
| (4.31) |
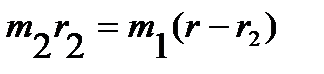 , , 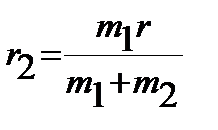 . .
| (4.32) |
Подстановка полученных выражений в уравнение (4.28) позволяет момент инерции I с межъядерным расстоянием 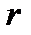 :
:
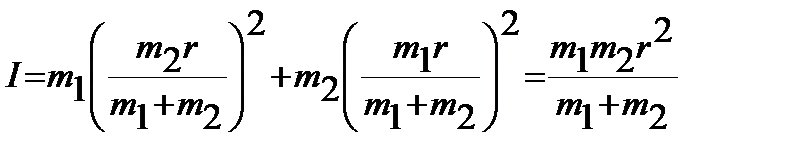 . .
| (4.33) |
Введение обозначения приведенной массы 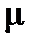 :
:
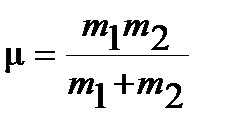
| (4.34) |
приводит к уравнению
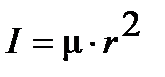 . .
| (4.35) |
Таким образом, двухатомную молекулу (рисунок 4.7а), вращающуюся вокруг оси 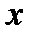 или
или 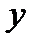 , проходящей через центр тяжести, можно упрощенно рассматривать как частицу с массой
, проходящей через центр тяжести, можно упрощенно рассматривать как частицу с массой 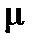 , описывающую круг с радиусом
, описывающую круг с радиусом 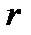 вокруг точки O (рисунок 4.7б).
вокруг точки O (рисунок 4.7б).
Вращение молекулы вокруг оси 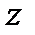 дает момент инерции, практически равный нулю, поскольку радиусы атомов значительно меньше межъядерного расстояния. Вращение относительно осей
дает момент инерции, практически равный нулю, поскольку радиусы атомов значительно меньше межъядерного расстояния. Вращение относительно осей 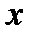 или
или 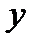 , взаимно перпендикулярных линии связи молекулы, приводит к равным по величине моментам инерции:
, взаимно перпендикулярных линии связи молекулы, приводит к равным по величине моментам инерции:

| (4.36) |
Решение уравнения Шредингера для вращательной энергии в приближении модели жесткого ротатора дает уравнение:
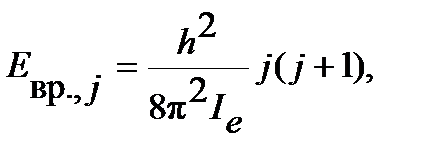
| (4.37) |
где 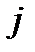 - вращательное квантовое число, принимающее только целочисленные значения
- вращательное квантовое число, принимающее только целочисленные значения
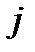 = 0, 1, 2…. В соответствии с правилом отбора для вращательного спектрадвухатомной молекулы изменение вращательного квантового числа при поглощении кванта энергии возможно лишь на единицу, т.е.
= 0, 1, 2…. В соответствии с правилом отбора для вращательного спектрадвухатомной молекулы изменение вращательного квантового числа при поглощении кванта энергии возможно лишь на единицу, т.е.
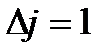 . .
| (4.38) |
Введение вращательной постоянной 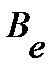 :
:
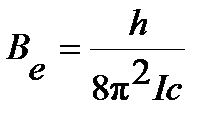
| (4.39) |
преобразует уравнение (4.37) в вид:
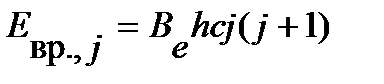 . .
| (4.40) |
Разность энергий двух соседних уровней может быть оценена по уравнению:
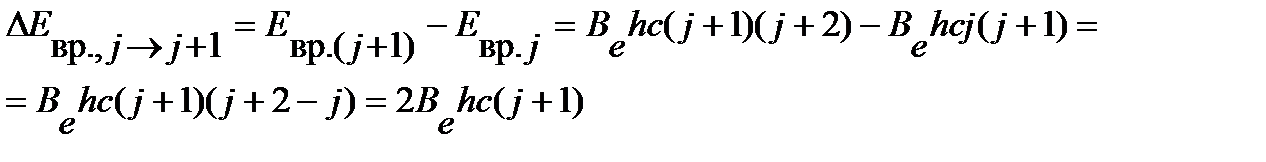
| (4.41) |
Из анализа уравнения (4.41) следует, что с ростом 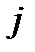 возрастает
возрастает 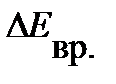 , т.е. вращательные уровни расходятся. Напротив, увеличение
, т.е. вращательные уровни расходятся. Напротив, увеличение 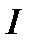 приводит к уменьшению
приводит к уменьшению 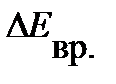 .
.
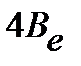
|
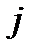
|
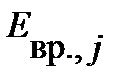 20
20 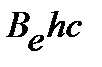 12
12 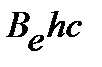 6
6 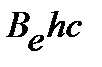 2
2 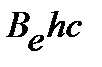
|
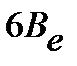
|
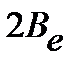
|
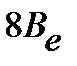
|
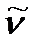
|
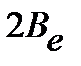
|
| а б |
Рисунок 4.5 – Расположение вращательных уровней энергии (а)
и схематичный вид вращательного спектра двухатомной молекулы (б)
в приближении жесткого ротатора
Поскольку
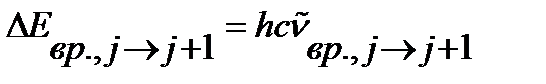 , ,
| (4.42) |
волновое число линии во вращательном спектре, соответствующей поглощению кванта при переходе с j уровня энергии на уровень j+1, можно вычислить по уравнению:
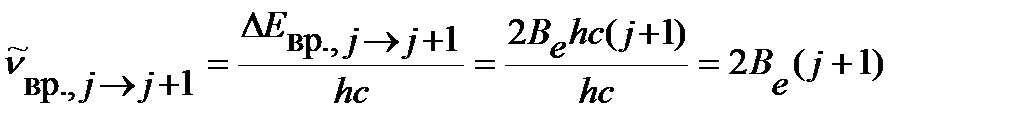 . .
| (4.43) |
Из этого уравнения следует, что с ростом 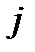 волновое число линии во вращательном спектре
волновое число линии во вращательном спектре 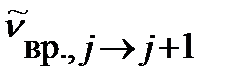 увеличивается, а интервал между линиями, тем не менее, остается постоянным:
увеличивается, а интервал между линиями, тем не менее, остается постоянным:
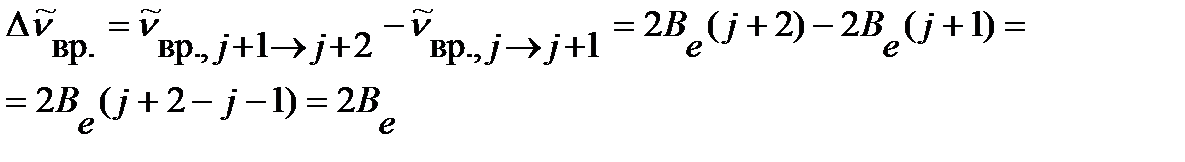
| (4.44) |
Таким образом, вращательный спектр в приближении модели жесткого ротатора представляет собой систему линий, находящихся на одном и том же расстоянии друг от друга (рисунок 4.5б). Примеры вращательных спектров двухатомных молекул, оцененных в модели жесткий ротатор, представлены на рисунке 4.6.
| а б |
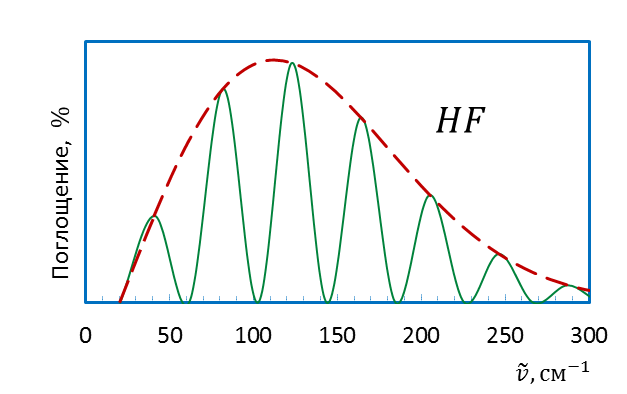
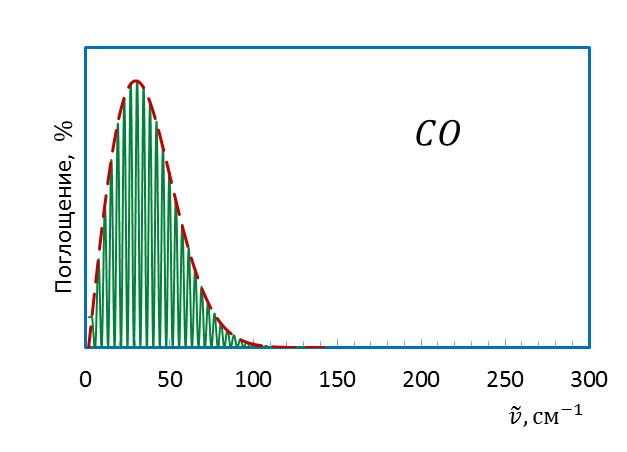
Рисунок 4.6 – Вращательныe спектры HF (а) и CO(б)
Для молекул галогеноводородов этот спектр смещен в дальнюю ИК область спектра, для более тяжелых молекул – в микроволновую.
Исходя из полученных закономерностей возникновения вращательного спектра двухатомной молекулы, на практике сперва определяют расстояние между соседними линиями в спектре 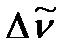 , из которого далее находят
, из которого далее находят 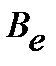 ,
, 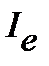 и
и 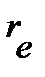 по уравнениям:
по уравнениям:
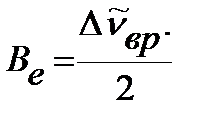 , ,
| (4.45) |
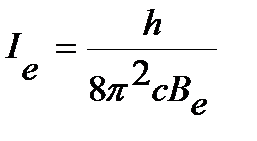 , ,
| (4.46) |
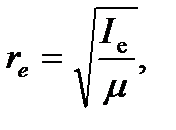
| (4.47) |
Реальная молекула не является жестким ротатором, т.к. при достаточно высоких скоростях вращения связь в молекуле несколько растягивается в результате действия центробежных сил. При этом момент инерции увеличивается, а расстояние между линиями вращательного спектра двухатомной молекулы с ростом j уменьшаются.
Учет поправки на центробежное искажение приводит к некоторому усложнению уравнения для вращательной энергии:
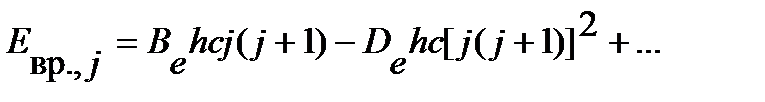
| (4.48) |
где 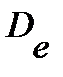 - постоянная центробежного искажения, связана с вращательной постоянной
- постоянная центробежного искажения, связана с вращательной постоянной 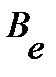 примерным соотношением
примерным соотношением 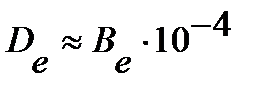 . Поправку следует учитывать лишь при очень больших j.
. Поправку следует учитывать лишь при очень больших j.
Для многоатомных молекул в общем случае возможно существование трех разных моментов инерции 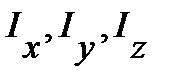 . При наличии в молекуле элементов симметрии моменты инерции могут совпадать или даже быть равными нулю. Например, для линейных многоатомных молекул (CO2, OCS, HCN и др.)
. При наличии в молекуле элементов симметрии моменты инерции могут совпадать или даже быть равными нулю. Например, для линейных многоатомных молекул (CO2, OCS, HCN и др.)
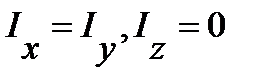
| (4.49) |
В случае несимметричных линейных молекул существуют по крайней мере две различных длины связи, например, в молекуле OCS 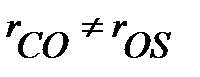 . Для определения межъядерных расстояний в таких молекулах используют спектры изотопных заместителей. При изменении приведенной массы изменяется момент инерции и положение линий в спектре. Наблюдается изотопный сдвиг
. Для определения межъядерных расстояний в таких молекулах используют спектры изотопных заместителей. При изменении приведенной массы изменяется момент инерции и положение линий в спектре. Наблюдается изотопный сдвиг
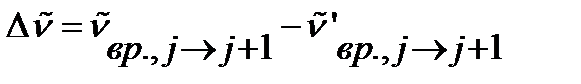 , ,
| (4.50) |
где 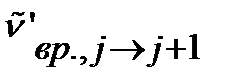 - положение линии, отвечающей вращательному переходу
- положение линии, отвечающей вращательному переходу 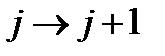 в изотопозамещенной молекуле.
в изотопозамещенной молекуле.
Для вычисления величины изотопного сдвига линии необходимо последовательно рассчитать приведенную массу 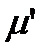 изотопозамещенной молекулы с учетом изменения атомной массы изотопа, момент инерции
изотопозамещенной молекулы с учетом изменения атомной массы изотопа, момент инерции 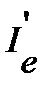 , вращательную постоянную
, вращательную постоянную 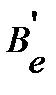 и положение линии в спектре молекулы по уравнениям (4.34), (4.35), (4.39) и (4.43), соответственно, или оценить отношение волновых чисел линий, отвечающих одному и тому же переходу в изотопозамещенной и неизотопозамещенной молекулах, и далее определить направление и величину изотопного сдвига по уравнению (4.50). Если межъядерное расстояние приближенно считать постоянным
и положение линии в спектре молекулы по уравнениям (4.34), (4.35), (4.39) и (4.43), соответственно, или оценить отношение волновых чисел линий, отвечающих одному и тому же переходу в изотопозамещенной и неизотопозамещенной молекулах, и далее определить направление и величину изотопного сдвига по уравнению (4.50). Если межъядерное расстояние приближенно считать постоянным 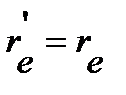 , то отношение волновых чисел соответствует обратному отношению приведенных масс:
, то отношение волновых чисел соответствует обратному отношению приведенных масс:
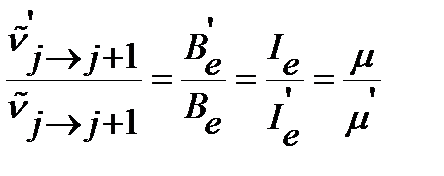
| (4.51) |
Экстремальный характер зависимости интенсивности полос во вращательном спектре двухатомной молекулы (рис.4.6) может быть связан с относительной «заселенностью» вращательных уровнейэнергии. Реальный вращательный спектр является спектром не отдельно взятой молекулы, а большой совокупности частиц с различными и быстро меняющимися в результате соударений энергиями. Распределение молекул по энергиям при постоянстве внешних параметров постоянно и определяется распределением Больцмана.
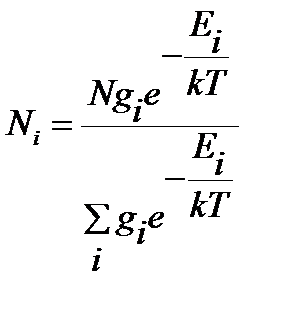 , ,
| (4.52) |
где 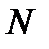 - общее число частиц,
- общее число частиц, 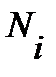 - число частиц на i - том уровне энергии при температуре T, k – постоянная Больцмана,
- число частиц на i - том уровне энергии при температуре T, k – постоянная Больцмана, 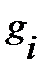 - статистический весили степень вырожденияi-того уровня энергии, характеризует вероятность нахождения частиц на данном уровне.
- статистический весили степень вырожденияi-того уровня энергии, характеризует вероятность нахождения частиц на данном уровне.
Для вращательного состояния заселенность уровня характеризуют обычно отношением числа частиц на j - том уровне энергии 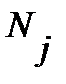 к числу частиц на нулевом уровне
к числу частиц на нулевом уровне 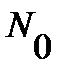 :
:
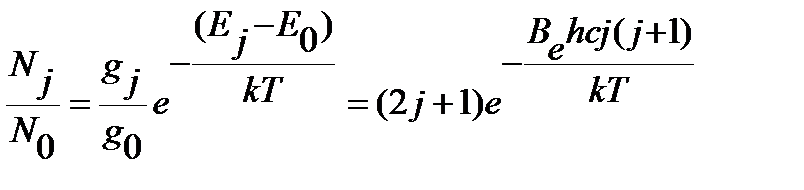 , ,
| (4.53) |
где 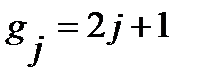 - статистический вес j-того вращательного уровня энергии, отвечает числу проекций количества движения вращающейся молекулы на ее ось – линию связи молекулы,
- статистический вес j-того вращательного уровня энергии, отвечает числу проекций количества движения вращающейся молекулы на ее ось – линию связи молекулы, 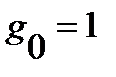 , энергия нулевого вращательного уровня
, энергия нулевого вращательного уровня 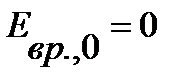 . Функция
. Функция 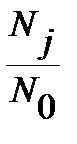 проходит через максимум при увеличении j, как иллюстрирует рисунок 4.7 на примере молекулы CO.
проходит через максимум при увеличении j, как иллюстрирует рисунок 4.7 на примере молекулы CO.
Экстремум функции соответствует уровню с максимальной относительной заселенностью, значение квантового числа которого можно вычислить по уравнению, полученному после определения производной функции в экстремуме:
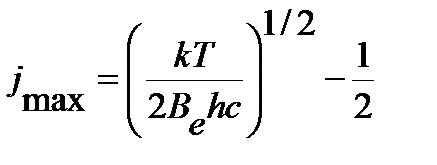 . .
| (4.54) |
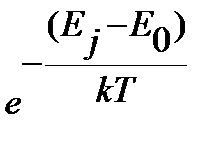
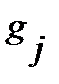
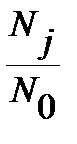
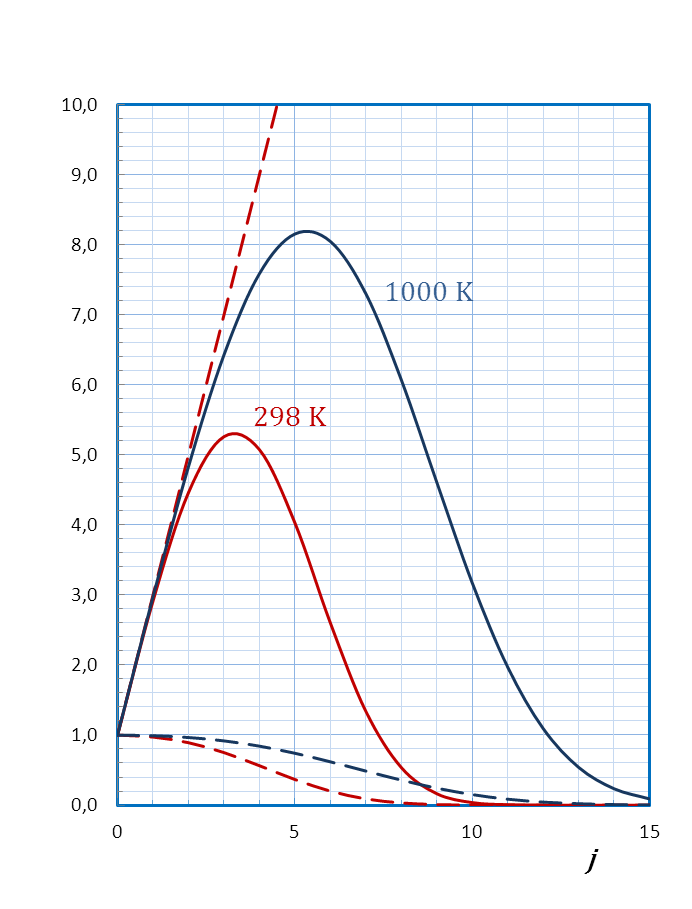
Рисунок 4.7 – Относительная заселенность вращательных уровней энергии
молекулы CO при температурах 298 и 1000 К
Пример. Во вращательном спектре HI определено расстояние между соседними линиями 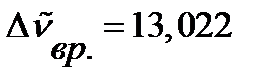 см-1. Рассчитайте вращательную постоянную, момент инерции и равновесное межъядерное расстояние в молекуле.
см-1. Рассчитайте вращательную постоянную, момент инерции и равновесное межъядерное расстояние в молекуле.
Решение
В приближении модели жесткого ротатора в соответствии с уравнением (4.45) определяем вращательную постоянную:
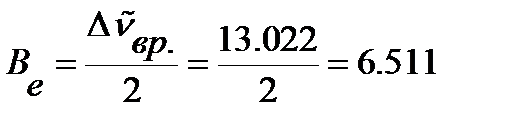 см-1.
см-1.
Момент инерции молекулы вычисляем из значения вращательной постоянной по уравнению (4.46):
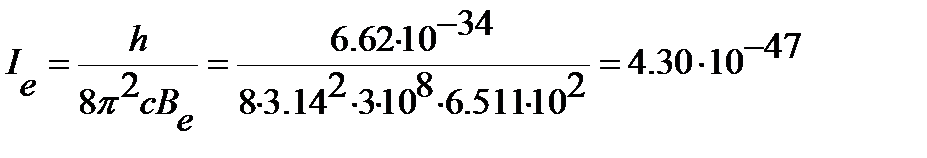 кг .м2.
кг .м2.
Для определения равновесного межъядерного расстояния используем уравнение (4.47), учитывая, что массы ядер водорода 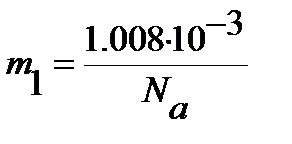 и йода
и йода 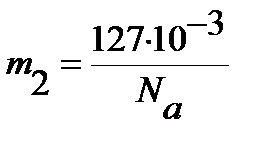 выражены в кг:
выражены в кг:
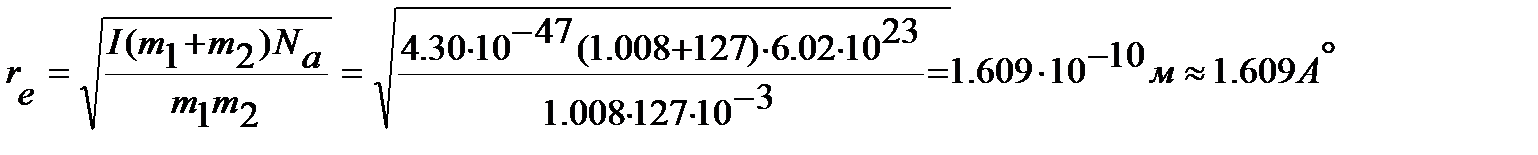
Пример. В дальней ИК-области спектра 1H35Cl обнаружены линии, волновые числа которых:
| N линии | |||||||
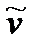 , см-1 , см-1
| 85.384 | 106.730 | 128.076 | 149.422 | 170.768 | 192.114 | 213.466 |
Определите усредненные значения момента инерции и межъядерного расстояния молекулы. Отнесите наблюдаемые линии в спектре к вращательным переходам.
Решение
Согласно модели жесткого ротатора разность волновых чисел 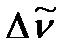 соседних линий вращательного спектра постоянна и равна 2
соседних линий вращательного спектра постоянна и равна 2 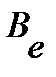 . Определим вращательную постоянную по среднему значению расстояний между соседними линиями в спектре:
. Определим вращательную постоянную по среднему значению расстояний между соседними линиями в спектре:
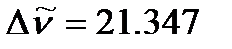 см-1,
см-1,
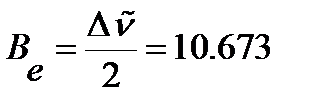 см-1
см-1
Находим момент инерции молекулы (уравнение (4.46)):
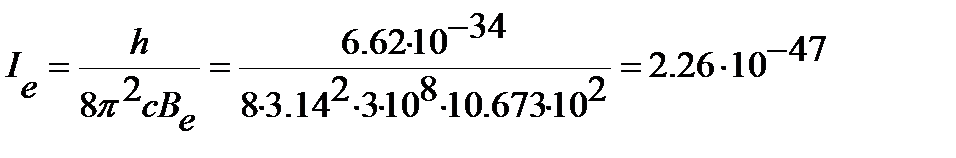 кг·м2
кг·м2
Рассчитываем равновесное межъядерное расстояние (уравнение (4.47)), принимая во внимание, что массы ядер водорода 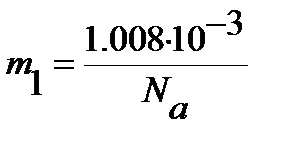 и хлора
и хлора 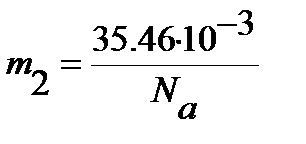 (выражены в кг):
(выражены в кг):

По уравнению (4.43) оцениваем положение линий во вращательном спектре 1H35Cl:
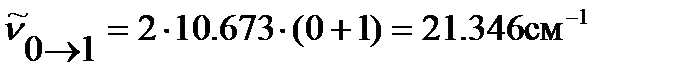
…
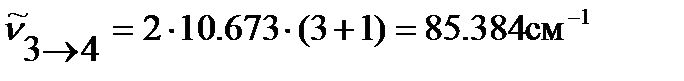
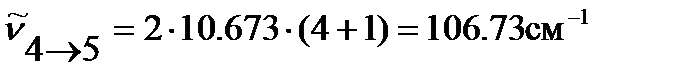 и т.д.
и т.д.
Соотносим рассчитанные значения волновых чисел линий с экспериментальными. Получается, что наблюдаемые во вращательном спектре 1H35Cl линии соответствуют переходам:
| N линии | |||||||
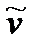 , см-1 , см-1
| 85.384 | 106.730 | 128.076 | 149.422 | 170.768 | 192.114 | 213.466 |
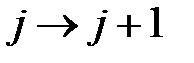
| 3 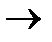 4 4
| 4 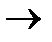 5 5
| 5 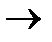 6 6
| 6 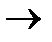 7 7
| 7 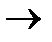 8 8
| 8 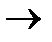 9 9
| 9 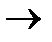 10 10
|
Пример. Определите величину и направление изотопного сдвига линии поглощения, отвечающей переходу с 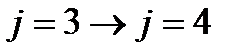 энергетический уровень, во вращательном спектре молекулы 1H35Cl при замещении атома хлора на изотоп 37Cl. Межъядерное расстояние в молекулах 1H35Cl и 1H37Cl считать одинаковым.
энергетический уровень, во вращательном спектре молекулы 1H35Cl при замещении атома хлора на изотоп 37Cl. Межъядерное расстояние в молекулах 1H35Cl и 1H37Cl считать одинаковым.
Решение
Для определения величины изотопного сдвига линии, отвечающей переходу 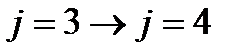 , рассчитываем приведенную массу
, рассчитываем приведенную массу 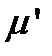 молекулы 1H37Cl с учетом изменения атомной массы 37Cl:
молекулы 1H37Cl с учетом изменения атомной массы 37Cl:
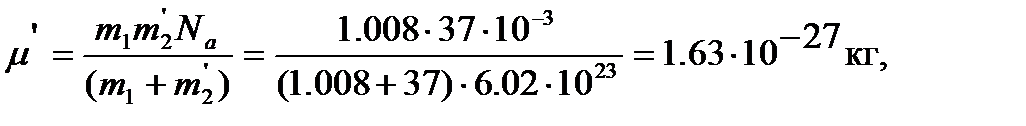
далее вычисляем момент инерции 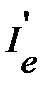 , вращательную постоянную
, вращательную постоянную 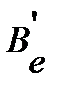 и положение линии
и положение линии 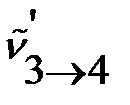 в спектре молекулы 1H37Cl и величину изотопного сдвига по уравнениям (4.35), (4.39), (4.43) и (4.50), соответственно.
в спектре молекулы 1H37Cl и величину изотопного сдвига по уравнениям (4.35), (4.39), (4.43) и (4.50), соответственно.
Иначе изотопный сдвиг можно оценить из отношения волновых чисел линий, отвечающих одному и тому же переходу в молекулах, (межъядерное расстояние считаем постоянным) и далее положение линии в спектре, используя уравнение (4.51).
Для молекул 1H35Cl и 1H37Cl отношение волновых чисел заданного перехода равно:
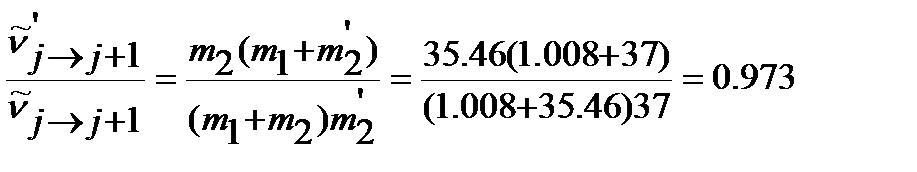
Для определения волнового числа линии изотопозамещенной молекулы подставляем найденное в предыдущем примере значение волнового числа перехода j → j+1 (3→4):
 .
.
Делаем вывод: изотопный сдвиг в низкочастотную или длинноволновую область составляет
85.384 - 83.049 = 2.335 см-1.
Пример. Рассчитайте волновое число и длину волны наиболее интенсивной спектральной линии вращательного спектра молекулы 1H35Cl. Соотнесите линию с соответствующим вращательным переходом.
Решение
Наиболее интенсивная линия во вращательном спектре молекулы связана с максимальной относительной заселенностью вращательного уровня энергии.
Подстановка найденного в предыдущем примере значения вращательной постоянной для 1H35Cl ( 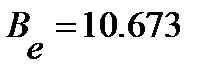 см-1) в уравнение (4.54) позволяет вычислить номер этого уровня энергии:
см-1) в уравнение (4.54) позволяет вычислить номер этого уровня энергии:
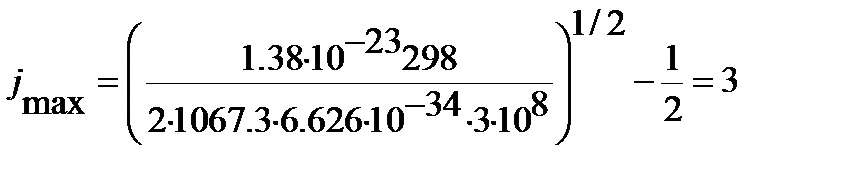 .
.
Волновое число вращательного перехода с этого уровня рассчитываем по уравнению (4.43):
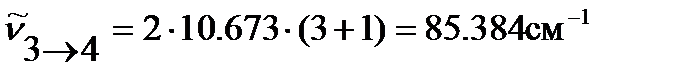 ,
,
Длину волны перехода находим из преобразованного относительно 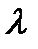 уравнения (4.11):
уравнения (4.11):
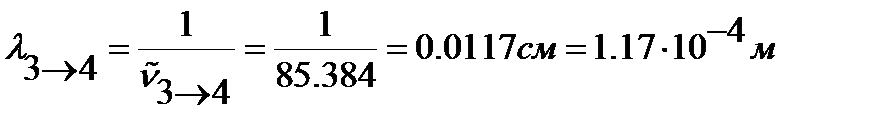 .
.
4.2.4 Многовариантное задание № 11 «Вращательные спектры двухатомных молекул»
1. Напишите квантово-механическое уравнение для расчета энергии вращательного движения двухатомной молекулы как жесткого ротатора.
2. Выведите уравнение для расчета изменения энергии вращения двухатомной молекулы как жесткого ротатора при переходе ее на соседний, более высокий квантовый уровень 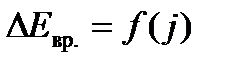 .
.
3. Выведите уравнение зависимости волнового числа вращательных линий в спектре поглощения двухатомной молекулы от вращательного квантового числа.
4. Выведите уравнение для расчета разности волновых чисел соседних линий во вращательном спектре поглощения двухатомной молекулы.
5. Рассчитайте вращательную постоянную 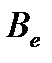 (в см-1 и м-1) двухатомной молекулы A по волновым числам двух соседних линий в длинноволновой инфракрасной области вращательного спектра поглощения молекулы (см. таблицу 4.3) .
(в см-1 и м-1) двухатомной молекулы A по волновым числам двух соседних линий в длинноволновой инфракрасной области вращательного спектра поглощения молекулы (см. таблицу 4.3) .
6. Определите энергию вращения молекулы A на первых пяти квантовых вращательных уровнях (Дж).
7. Вычертите схематически энергетические уровни вращательного движения двухатомной молекулы как жесткого ротатора.
8. Нанесите пунктиром на эту схему вращательные квантовые уровни молекулы, не являющейся жестким ротатором.
9. Выведите уравнение для вычисления равновесного межъядерного расстояния на основании разности волновых чисел соседних линий во вращательном спектре поглощения.
10. Определите момент инерции 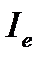 (кг.м2) двухатомной молекулы A.
(кг.м2) двухатомной молекулы A.
11. Рассчитайте приведенную массу 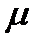 (кг) молекулы A.
(кг) молекулы A.
12. Вычислите равновесное межъядерное расстояние 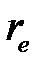 (
( 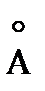 ) молекулы A. Сопоставьте полученное значение со справочными данными.
) молекулы A. Сопоставьте полученное значение со справочными данными.
13. Отнесите наблюдаемые линии во вращательном спектре молекулы A к вращательным переходам.
14. Рассчитайте волновое число спектральной линии, отвечающей вращательному переходу с уровня j для молекулы A (см. таблицу 4.3).
15. Вычислите приведенную массу 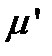 (кг) изотопозамещенной молекулы B.
(кг) изотопозамещенной молекулы B.
16. Рассчитайте волновое число спектральной линии, связанной с вращательным переходом с уровня j для молекулы B (см. таблицу 4.3). Межъядерные расстояния в молекулах A и B считать равными.
17. Определите величину и направление изотопного сдвига во вращательных спектрах молекул A и B для спектральной линии, отвечающей переходу с вращательного уровня j.
18. Объясните причину немонотонного изменения интенсивности линий поглощения по мере увеличения энергии вращения молекулы
19. Определите квантовое число вращательного уровня, отвечающего наибольшей относительной заселенности. Рассчитайте длины волн наиболее интенсивных спектральных линий вращательных спектров молекул A и B.
Таблица 4.3 – Варианты заданий
| Вариант | Молекула A | Под вариант | 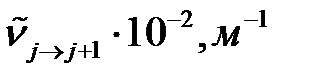
| j | Молекула B | |
| LiH | 60.12 | 75.15 | Li2H | |||
| 180.36 | 195.39 | 8LiH | ||||
| 195.39 | 210.42 | 6Li3H | ||||
| 105.21 | 120.24 | Li3H | ||||
| 120.24 | 135.27 | 6LiH | ||||
| 90.18 | 105.21 | 6Li2H | ||||
| BCl | 4.104 | 5.472 | B37Cl | |||
| 8.208 | 9.576 | 10BCl | ||||
| 9.576 | 10.944 | B37Cl | ||||
| 10.944 | 12.312 | 10B37Cl | ||||
| 12.312 | 13.68 | 10BCl | ||||
| 17.784 | 19.152 | B37Cl | ||||
| BeH | 103.15 | 123.78 | Be2H | |||
| 82.52 | 103.15 | Be3H | ||||
| 226.93 | 247.56 | 5BeH | ||||
| 247.56 | 268.19 | 11BeH | ||||
| 185.67 | 206.3 | 13BeH | ||||
| 206.3 | 226.93 | 16BeH | ||||
| CO | 11.534 | 15.379 | 13CO | |||
| 23.068 | 26.913 | C17O | ||||
| 26.913 | 30.757 | 17CO | ||||
| 30.757 | 34.602 | C18O | ||||
| 34.602 | 38.447 | 14CO | ||||
| 53.825 | 57.670 | 15CO | ||||
| HBr | 33.88 | 50.82 | 3HBr | |||
| 152.48 | 169.42 | 2HBr | ||||
| 203.30 | 220.25 | H77Br | ||||
| 186.36 | 203.30 | H85Br | ||||
| 169.42 | 186.36 | H84Br | ||||
| 220.25 | 237.19 | H82Br | ||||
| HCl | 169.44 | 190.62 | 2HCl | |||
| 232.98 | 254.16 | 3HCl | ||||
| 127.08 | 148.26 | H37Cl | ||||
| 105.90 | 127.08 | 3HCl | ||||
| 254.16 | 275.34 | 2H37Cl | ||||
| 148.26 | 169.44 | 3H37Cl | ||||
| LiF | 5.38 | 8.07 | 6LiF | |||
| 24.21 | 26.90 | 6Li18F | ||||
| 16.14 | 18.83 | Li18F | ||||
| 13.45 | 16.14 | 6LiF | ||||
| 21.52 | 24.21 | 6Li18F | ||||
| 18.83 | 21.52 | 6LiF |
Продолжение таблицы 4.3
| Вариант | Молекула A | Под вариант | 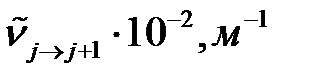
| j | Молекула B | |
| HI | 39.066 | 52.088 | 2HI | |||
| 91.154 | 104.176 | 3HI | ||||
| 143.242 | 156.264 | 2H129I | ||||
| 104.176 | 117.198 | 3H131I | ||||
| 130.220 | 143.242 | H129I | ||||
| 117.198 | 130.220 | H131I | ||||
| CsI | 0.0944 | 0.1416 | Cs125I | |||
| 0.5192 | 0.5664 | 135Cs125I | ||||
| 0.6608 | 0.7080 | 134Cs129I | ||||
| 0.6136 | 0.6608 | Cs129I | ||||
| 0.5664 | 0.6136 | 135CsI | ||||
| 0.7080 | 0.7552 | 134CsI | ||||
| OH | 189.20 | 227.04 | O2H | |||
| 416.24 | 454.08 | 17O2H | ||||
| 491.92 | 529.76 | 17OH | ||||
| 567.60 | 605.44 | O3H | ||||
| 529.76 | 567.60 | 18O2H | ||||
| 454.08 | 491.92 | 18OH | ||||
| NaH | 29.40 | 39.20 | Na2H | |||
| 58.80 | 68.60 | 24Na2H | ||||
| 127.40 | 137.20 | 22NaH | ||||
| 98.00 | 107.80 | 24NaH | ||||
| 88.20 | 98.00 | 22Na3H | ||||
| 137.20 | 147.00 | Na3H | ||||
| SiH | 45.01 | 59.99 | Si2H | |||
| 165.00 | 180.00 | Si3H | ||||
| 105.00 | 120.00 | 29SiH | ||||
| 195.00 | 210.00 | 29Si2H | ||||
| 225.00 | 240.00 | 30SiH | ||||
| 210.00 | 225.00 | 30Si3H | ||||
| HF | 123.15 | 164.00 | 2HF | |||
| 205.25 | 246.30 | 3H18F | ||||
| 246.30 | 287.35 | 2H18F | ||||
| 492.60 | 533.65 | 3HF | ||||
| 533.65 | 574.70 | H18F | ||||
| 369.45 | 410.50 | 2HF | ||||
| NO | 17.05 | 20.46 | N18O | |||
| 44.33 | 47.74 | N17O | ||||
| 34.10 | 37.51 | 15N18O | ||||
| 30.69 | 34.10 | 15NO | ||||
| 40.92 | 44.33 | 15N17O | ||||
| 37.51 | 40.92 | 13NO |
Продолжение таблицы 4.3
| Вариант | Молекула A | Под вариант | 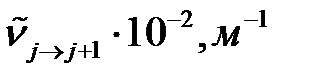
| j | Молекула B | |
| SO | 8.64 | 10.08 | S18O | |||
| 18.72 | 20.16 | 34SO | ||||
| 14.40 | 15.84 | S17O | ||||
| 17.28 | 18.72 | 36SO | ||||
| 15.84 | 17.28 | 33S17O | ||||
| 12.96 | 14.40 | 33SO | ||||
| ClO | 6.25 | 7.50 | 37ClO | |||
| 13.75 | 15.00 | Cl17O | ||||
| 18.75 | 20.00 | 37Cl18O | ||||
| 12.50 | 13.75 | Cl18O | ||||
| 15.00 | 16.25 | 37Cl17O | ||||
| 10.00 | 11.25 | 37ClO | ||||
| CN | 3.80 | 7.60 | 13C N | |||
| 15.20 | 19.00 | 13C15N | ||||
| 38.00 | 41.80 | 14CN | ||||
| 22.80 | 26.60 | C13N | ||||
| 53.20 | 57.00 | C15N | ||||
| 30.40 | 34.20 | 13C13N | ||||
| SH | 95.95 | 115.14 | S2H | |||
| 211.09 | 230.28 | 33S2H | ||||
| 268.66 | 287.85 | 33S3H | ||||
| 191.90 | 211.09 | 34S2H | ||||
| 172.71 | 191.90 | 34S3H | ||||
| 153.52 | 172.71 | S3H | ||||
| FO | 8.84 | 11.05 | F18O | |||
| 22.10 | 24.31 | F17O | ||||
| 15.47 | 17.68 | F18O | ||||
| 19.89 | 22.10 | 18FO | ||||
| 17.68 | 19.89 | 18F18O | ||||
| 13.26 | 15.47 | 18F17O | ||||
| HB | 144.24 | 168.28 | 2HB | |||
| 216.36 | 240.4 | 3HB | ||||
| 240.4 | 264.44 | 2H10B | ||||
| 264.44 | 288.48 | 3H10B | ||||
| 96.16 | 120.2 | H10B | ||||
| 120.2 | 144.24 | 3HB | ||||
| PH | 51.74 | 69.04 | P2H | |||
| 138.08 | 155.34 | P3H | ||||
| 224.38 | 241.64 | P2H | ||||
| 103.56 | 120.82 | 30P3H | ||||
| 120.82 | 138.08 | 30P2H | ||||
| 172.6 | 189.86 | P2H |
Продолжение таблицы 4.3
| Вариант | Молекула A | Под вариант | 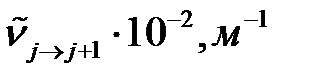
| j | Молекула B | |
| BeO | 13.20 | 16.50 | Be18O | |||
| 52.8 | 56.10 | Be17O | ||||
| 39.6 | 42.90 | Be18O | ||||
| 26.4 | 29.70 | 7BeO | ||||
| 46.2 | 49.50 | 7Be18O | ||||
| 19.8 | 23.10 | 7Be17O | ||||
| NH | 133.32 | 166.65 | N2H | |||
| 433.29 | 466.62 | N3H | ||||
| 333.3 | 366.63 | 15NH | ||||
| 399.96 | 433.29 | 13NH | ||||
| 299.97 | 333.30 | 15N2H | ||||
| 366.63 | 399.96 | 15N3H | ||||
| 2H81Br | 16.9795 | 25.4640 | 2H 79Br | |||
| 59.416 | 67.90 | 3H 79Br | ||||
| 110.344 | 118.83 | 2H 80Br | ||||
| 76.392 | 84.88 | 3H<
Дата добавления: 2021-01-26; просмотров: 2081; |











