ХИМИЧЕСКАЯ КИНЕТИКА
Важнейшей количественной характеристикой химического процесса является скорость химической реакции. Под средней удельнойскоростью химическойреакции, определенной по i-тому компоненту, понимают изменение количества этого компонента за единицу времени в единице реакционного пространства. Для гомогенной реакции за реакционное пространство принимается объем. Тогда для бесконечно малого промежутка мгновенную удельную скорость реакции (υi ) можно выразить:
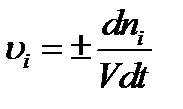 , (6.1)
, (6.1)
где ni –количество i-го вещества, в молях;
V – объем реакционной смеси;
t – время.
Так как скорость всегда положительна, то для веществ, расходующихся в ходе реакции, dni < 0и 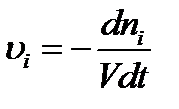 .
.
Если гомогенная реакция протекает в замкнутой системе при V = const , то в этом случае V можно внести под знак дифференциала и, учитывая, что ni/V = ci, уравнение (6.1) можно представить в виде:
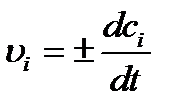 , (6.2)
, (6.2)
где сi - концентрация вещества (обычно в моль/л).
Для определения скорости реакции по i – тому компоненту необходимо знать, как изменяется концентрация этого компонента во времени в ходе реакции. График зависимости концентрации вещества от времени называют кинетической кривой. Скорость реакции в любой момент времени определяется как тангенс угла наклона касательной, проведенной к кинетической кривой в данный момент времени.
Скорость химической реакции зависит от целого ряда факторов. При заданных внешних условиях (температура, давление, среда, в которой происходит реакция) скорость является функцией концентрации реагирующих веществ. Для протекания химической реакции реагирующие частицы должны столкнуться или, по крайней мере, сблизиться друг с другом. Число столкновений частиц пропорционально их концентрации. Тогда для скорости химической реакции
a А + b B ® продукты
можно записать уравнение:
υ = 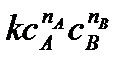 (6.3)
(6.3)
Уравнение (6.3) называется кинетическим уравнением. Это основное уравнение формальной гомогенной кинетики. Параметр k – коэффициент пропорциональности – константа скорости химической реакции. Константа k характеризует скорость химической реакции при концентрациях реагирующих веществ, равных единице: k = υпри сА = сB = 1.
Константа скорости химической реакции зависит от физико-химических свойств веществ, участвующих в реакции, от среды, в которой она происходит, от наличия катализатора или ингибитора, от температуры, и не зависит от концентрации реагирующих веществ. Поэтому, если хотят сравнивать скорости химических реакций, то всегда сравнивают константы скорости этих реакций.
Параметры nАи nB называют порядком реакциипо веществу А и B, соответственно. Общий (полный) порядок реакции n = nА+ nB .
Порядки реакции – это эмпирические показатели степени в кинетическом уравнении, которые находятся из экспериментальных данных. Порядки сложных реакций, состоящих из нескольких стадий, могут быть любыми: целыми, дробными, нулевыми, отрицательными. Порядки ni, как правило, не совпадают со стехиометрическими коэффициентами (а и b). Причина этого заключается в том, что химические реакции обычно идут в несколько стадий. Простые реакции протекают в одну элементарную стадию. Сложные химические реакции состоят из нескольких элементарных стадий.
Молекулярностьюотдельной стадии химической реакции называют наименьшее число частиц, которые должны столкнуться, чтобы произошла данная химическая реакция. Это целое число – 1, 2, 3, которое совпадает с суммой стехиометрических коэффициентов для данной стадии химической реакции. Молекулярность не может быть больше 3, так как вероятность одновременного столкновения четырех частиц в данной точке пространства крайне мала. Для химической реакции, протекающей в одну стадию, порядки реакции по веществам совпадают со стехиометрическими коэффициентами, а общий порядок совпадает с молекулярностью реакции.
Если в сложной реакции скорость какой-либо стадии значительно меньше, чем скорость других стадий, то такая стадия называется лимитирующей, и скорость этой стадии определяет скорость всего процесса. В этом случае молекулярность лимитирующей стадии совпадает с общим порядком реакции.
Наиболее часто химические реакции протекают по первому или второму порядку. Первый, второй и третий порядки реакций наблюдаются в двух случаях:
1. Реакция простая, протекающая в одну стадию.
2. Сложная реакция имеет лимитирующую стадию.
Число простых реакций очень мало. Значительно больше реакций, имеющих лимитирующую стадию. Именно скорость этой стадии определяет общую скорость химической реакции. Тогда порядок химической реакции будет равен порядку лимитирующей стадии.
Используя основное уравнение кинетики (6.3), можно получить выражение для расчета константы скорости химической реакции различных порядков. Алгоритм решения этой задачи следующий:
а) Записывают кинетическое уравнение.
б) Разделяют переменные с и t.
в) Интегрируют полученное уравнение в пределах от начала реакции (t = 0) и начальной концентрации с0 до момента времени τ и концентрации с.
Для реакции первого порядка основное кинетическое уравнение имеет вид
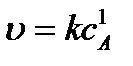 или
или 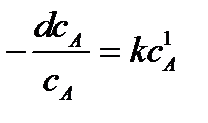
После интегрирования получают уравнение
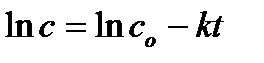 или
или 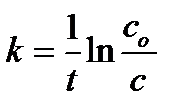 (6.4)
(6.4)
Единицы измерения k – c-1 или мин -1.
Из уравнения (6.4) следует, что зависимость lnc от t линейна.
Период полупревращения(t1/2) – это время, за которое концентрация исходного реагирующего вещества уменьшается вдвое. Для реакции первого порядка
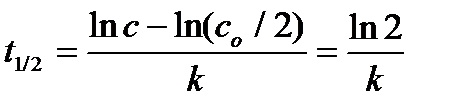
Следовательно, период полупревращения реакций первого порядка не зависит от начальной концентрации реагирующего вещества.
Таким образом, если анализ экспериментальных данных показывает, что для исследуемой реакции зависимость lnc от времени линейна, и период полупревращения не зависит от начальной концентрации, то данная реакция первого порядка.
Реакции второго порядка в общем виде можно записать как
2А → В + С или А + D → P + Q
В частном случае при сА= сD = с кинетическое уравнение для реакции второго порядка будет иметь вид :
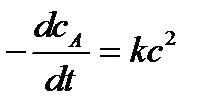 .
.
В результате интегрирования получают уравнение для вычисления константы скорости реакции второго порядка
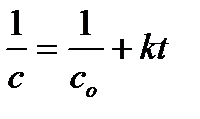 или
или 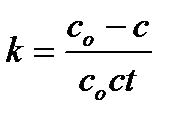 (6.5)
(6.5)
Единицы измерения k –л ∙ моль-1 ∙ с-1 или л ∙ моль-1 ∙ мин -1.
Для реакций второго порядка линейная зависимость будет в координатах 1/с от t .
Из уравнения (6.5) следует, что для реакции второго порядка
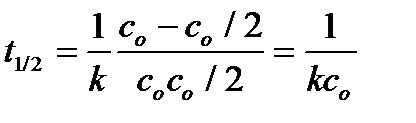 ,
,
то есть период полупревращения обратно пропорционален исходной концентрации.
Следовательно, если для исследуемой реакции зависимость 1/с от времени линейна, и период полупревращения обратно пропорционален исходной концентрации, то это реакция второго порядка.
Пример: Определим порядок и константу скорости реакции
2NO2 = 2NO + O2, если концентрация исходного вещества изменялась во времени следующим образом:
| t, с | ||||||||
| с, моль×л-1 | 0.0225 | 0.0158 | 0.0132 | 0.0093 | 0.0072 | 0.0059 | 0.0050 | 0.0043 |
Решение:
Константа скорости реакции не зависит от концентрации реагирующих веществ, поэтому эта величина не должна изменяться со временем. Используя экспериментальные данные и уравнения (6.4) и (6.5), рассчитаем константы скорости реакции в разные моменты времени. Результаты расчета приведены в таблице. Константа kI вычислена по уравнению (6.4), т.е. в предположении, что реакция 1-го порядка. Константа kII – по уравнению (6.5), т.е. предполагалось, что реакция 2-го порядка.
| t, с | ||||||||
| с, моль×л-1 | 0.0225 | 0.0158 | 0.0132 | 0.0093 | 0.0072 | 0.0059 | 0.0050 | 0.0043 |
| lnc | -3.79 | -4.15 | -4.33 | -4.68 | -4.93 | -5.13 | -5.30 | -5.45 |
| 1/c | 44.44 | 63.29 | 75.76 | 107.53 | 138.89 | 169.43 | 232.56 | |
| kI, с-1 | 0.118 | 0.107 | 0.088 | 0.076 | 0.067 | 0.060 | 0.055 | |
| kII, л×моль-1×с-1 | 6.28 | 6.26 | 6.31 | 6.30 | 6.25 | 6.22 | 6.27 |
Как видно из результатов расчета, константа является постоянной величиной при вычислении по уравнению (6.5), т.е. реакция 2-го порядка. kср= 6.27 л×моль-1×с-1. Графическая зависимость, построенная в координатах 1/с = f(t), будет линейной.
Зная величину константы скорости реакции, по уравнениям (6.4) и (6.5) легко вычислить концентрацию реагирующего вещества в любой момент времени. Это даст возможность рассчитать время, в течение которого следует проводить реакцию.
Пример: Используя вычисленное значение константы скорости химической реакции (kср= 6.27 л×моль-1×с-1) для реакции 2NO2 = 2NO + O2 , определим:
1. Время, за которое прореагирует 20% исходного вещества.
Так как реакция 2-го порядка, то для расчета используем уравнение (6.5). Если прореагировало 20% от исходной концентрации, то концентрация вещества в искомый момент времени составит 0.8со. Тогда
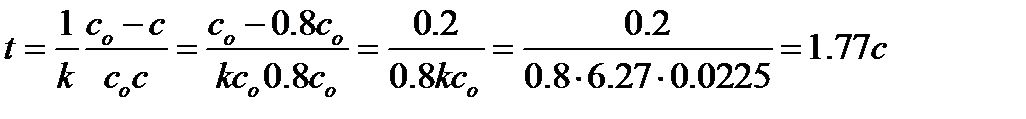
2. Период полупревращения реакции.
Для реакции 2-го порядка
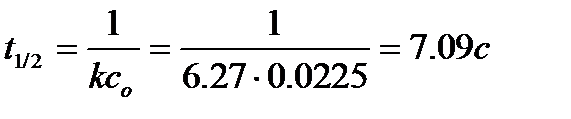
3. Сколько прореагировало исходного вещества к моменту времени 1мин.
Из уравнения (6.5)
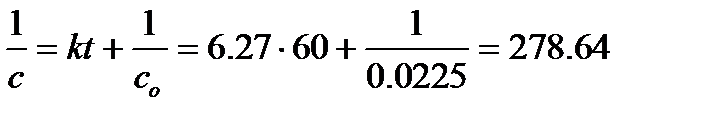 и с = 3.59×10-3 моль×л-1.
и с = 3.59×10-3 моль×л-1.
Таким образом, концентрация исходного вещества к моменту времени 1 мин составила 3.59×10-3 моль×л-1. Следовательно, прореагировало  моль×л-1, т.е. 84 % от исходной концентрации.
моль×л-1, т.е. 84 % от исходной концентрации.
Скорость гомогенной химической реакции, как правило, резко возрастает с ростом температуры. Иногда зависимость скорости реакции от температуры характеризуют величиной температурного коэффициента γ (температурный коэффициент Вант-Гоффа), который показывает, во сколько раз возрастает скорость химической реакции (константа скорости) при увеличении температуры на 10 градусов:
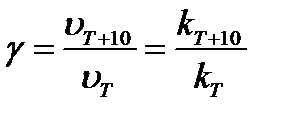 , (6.6)
, (6.6)
где υ и kT – скорость и константа скорости реакции при температуре Т;
υT+10 и kT+10 – скорость и константа скорости реакции при температуре Т+10.
Обычно γ = 2 ÷ 4.
Если температура возрастает больше, чем на десять градусов, то
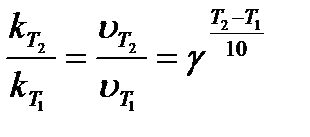 (6.7)
(6.7)
Пример: Константа скорости реакции димеризации бутадиена в газовой фазе при Т1=503К равна 5.31×10-4 л×моль-1×с-1, а при Т2=540К составляет 2.43×10--3 л×моль-1×с-1. Определим температурный коэффициент Вант-Гоффа и рассчитаем во сколько раз увеличивается скорость реакции при увеличении температуры на 15 градусов.
Решение:
Константы скорости реакции определены при температурах, отличающихся на 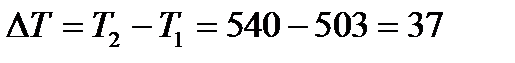 . Следовательно
. Следовательно
 . Тогда
. Тогда 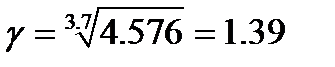 .
.
При увеличении температуры на 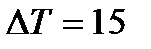 скорость реакции возрастет в
скорость реакции возрастет в 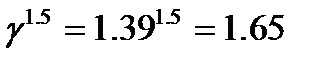 раз.
раз.
Аррениус предположил, что уравнение для зависимости константы скорости реакции от температуры аналогично уравнению изобары химической реакции:
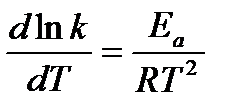 , (6.8)
, (6.8)
где Ea – энергия активации реакции
Энергия активации- та минимальная энергия, которой должны обладать реагирующие частицы, чтобы при их столкновении могла бы произойти химическая реакция.
Таким образом, Аррениусом впервые было введено представление о том, что не всякое столкновение частиц приводит к возникновению химической реакции, а только столкновение активных частиц, обладающих энергией активации Еа.
Обычно считают, что Еа не зависит от температуры. Однако очень точные измерения показывают, что это справедливо лишь в первом приближении. Если в данном температурном интервале Еа = const, то, интегрируя уравнение (6.8), получим:
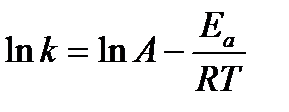 или k = А exp(– Ea / RT), (6.9)
или k = А exp(– Ea / RT), (6.9)
где А – предэкспоненциальный множитель (предэкспонента).
Численное значение этого коэффициента может быть рассчитано из теории элементарного акта химической реакции. Как правило, А слабо зависит от температуры. Тогда в первом приближении можно считать, что зависимость ln k от 1/Т линейная, и величину энергии активации можно определить как тангенс угла наклона экспериментальной зависимости ln k = f (1/Т):
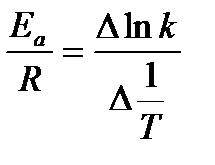 (6.10)
(6.10)
Энергию активации можно также определить, зная константы скорости при двух температурах:
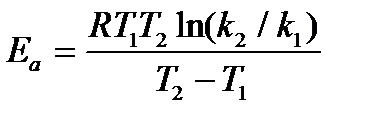 (6.11)
(6.11)
Пример:Для реакции С2Н2 +Н2 = С2Н4 при Т1= 773К константа скорости k1 = 1,14×10–2 (л×моль–1ּс–1), а при Т2 = 825К значение k2 = 7,11×10–2 (л×моль–1ּс–1). Определить энергию активации, предэкспоненциальный множитель А и константу скорости химической реакции при Т = 800К.
Решение.
Из уравнения (7.11) следует, что
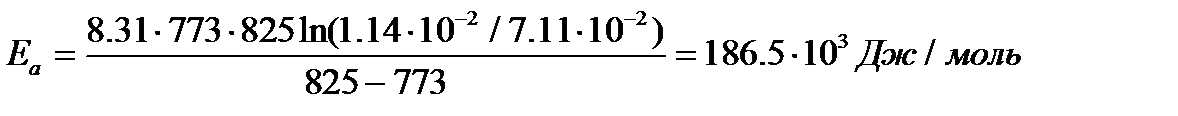
Используя уравнение (6.9), получим
ln А = ln k1 + Ea / RT1 = ln 1,14ּ10–2 + 186500 / (8,31 ּ 773) = 24,56
или А = 4,6×1010 л×моль–1ּс–1 .
Тогда при Т = 800 К
ln k = ln А – Ea / RT = 24,56 – 186500 / (8,31 ּ 800) = – 3,49
или k = 3.04× 10–2 л×моль–1ּс–1 .
6.1 Многовариантное задание № 14 «Расчет кинетических параметров гомогенных химических реакций»
Используя экспериментальные данные по изменению концентрации исходного вещества во времени для реакции В, заданной в таблице 6.1, выполните следующие действия:
1. Постройте графики зависимости концентрации сисходного вещества от времени t в координатах lnс = f(t) и 1/с = f(t). По виду графика определите порядок реакции.
2. Рассчитайте константу скорости реакции В.
3. Вычислите концентрацию исходного вещества и продуктов реакции В через t1 с от начала реакции.
4. Рассчитайте время, за которое прореагирует 10% исходного вещества.
5. Определите период полупревращения реакции.
Дата добавления: 2021-01-26; просмотров: 1005;











