ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ТЕРМОДИНАМИКИ
Статистическая термодинамика позволяет рассчитать термодинамические функции газообразных веществ (внутреннюю энергию, энтальпию, теплоемкость, энтропию, энергии Гиббса и Гельмгольца) на основании известных молекулярных констант, т.е. характеристик отдельной молекулы. Для этой цели в статистической термодинамике вводится функция
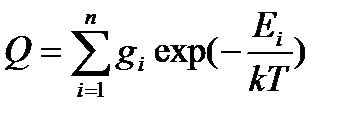
| (5.1) |
Эта функция называется суммой по состояниямили функцией распределения, так как она показывает, как распределяются молекулы идеального газа по соответствующим значениям энергии. В принципе состоянию с одним значением энергии 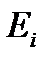 может отвечать несколько микросостояний. Число таких микросостояний
может отвечать несколько микросостояний. Число таких микросостояний 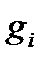 называется статистическим весом, а сами состояния – вырожденными.
называется статистическим весом, а сами состояния – вырожденными.
Внутреннюю энергию 1 моля идеального газа, находящегося в системе при постоянном объеме (V=const), можно выразить через сумму по состояниям
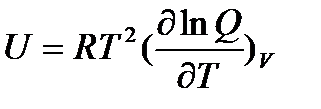
| (5.2) |
Так как все термодинамические функции связаны между собой, то, используя уравнение (5.2), можно получить уравнения для других термодинамических функций. Так, например, изохорная теплоемкость газа
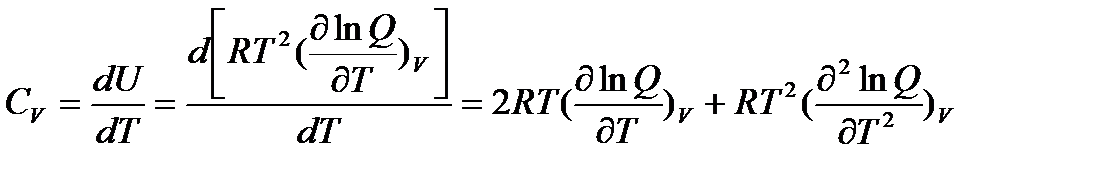
| (5.3) |
Абсолютная энтропия
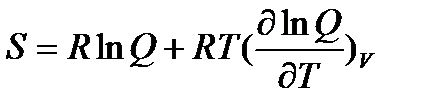
| (5.4) |
Энергия Гельмгольца
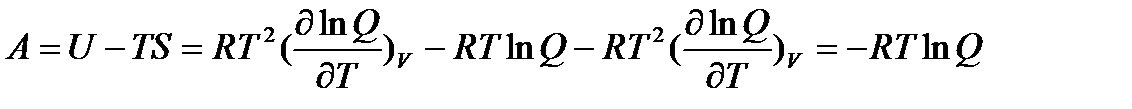
| (5.5) |
Полная энергия газовой молекулы складывается из энергии поступательного движения центра тяжести молекулы Епост, вращательной энергии атомов вокруг центра тяжести Евр, колебательной энергии Екол и электронной энергии Еэл , т.е.
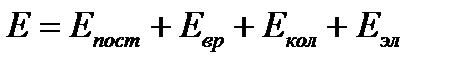
|
Поэтому нетрудно показать, что
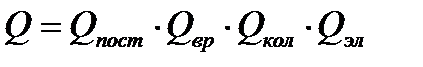
|
или
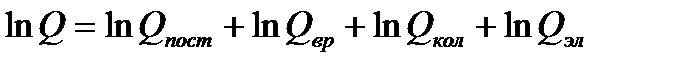
| (5.6) |
Соответственно, термодинамические функции можно представить как сумму составляющих, относящихся к различным видам движения.
Используя данные по строению отдельной молекулы, можно вычислить составляющие суммы по состояниям для отдельных видов движения.
Для поступательного движения эта величина зависит от массы частицы М, температуры Т и давления Р (или объема V):
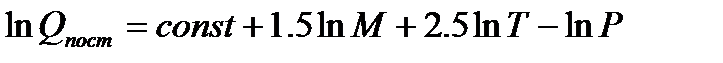 (5.7)
(5.7)
или
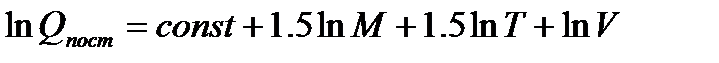
Пример:. Рассчитаем значение поступательной составляющей суммы по состояниям для молекулярного водорода при Р=1 атм и Т=298К.
Решение:
Если молярную массу М выражать в г/моль, а давление Р в Па, то в уравнении (5.7) const=8.8612 и тогда
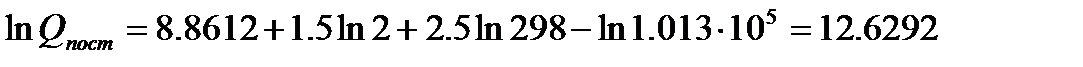
Для вращательного движения двухатомной или линейной многоатомной молекулы составляющая суммы по состояниям зависит от величины момента инерции молекулы I, температуры и коэффициента симметрии s:
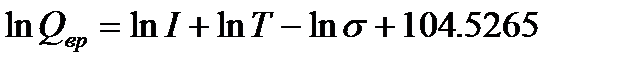 (5.8)
(5.8)
Для вращательного движения многоатомной нелинейной молекулы типа ассиметричного волчка, имеющего различающиеся моменты инерции относительно всех трех осей симметрии, составляющая суммы по состояниям равна
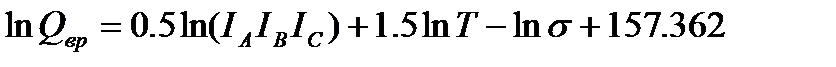 (5.9)
(5.9)
Пример:. Рассчитаем значение вращательной составляющей суммы по состояниям для молекулы водорода при Т=298К.
Решение:.
Для двухатомной молекулы момент инерции рассчитывается по формуле
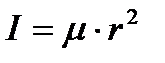 ,
,
где 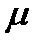 - приведенная масса.
- приведенная масса.
Для молекулы водорода
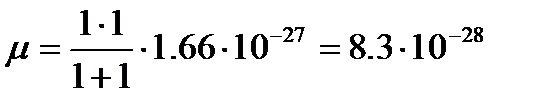 кг
кг
Равновесное межъядерное расстояние для молекулы водорода 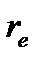 =0.741×10-10м (см.[2], табл. 107, с.177), следовательно, момент инерции равен
=0.741×10-10м (см.[2], табл. 107, с.177), следовательно, момент инерции равен
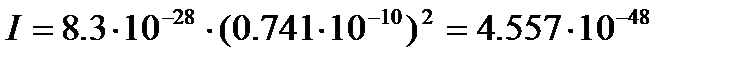 кг×м2
кг×м2
Коэффициент симметрии для линейных молекул  =2. И тогда
=2. И тогда
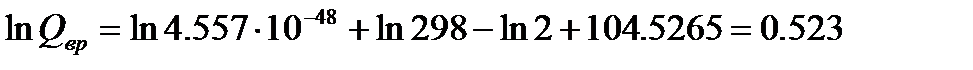
Колебательную составляющую суммы по состояниям можно вычислить по уравнению:
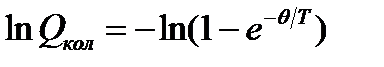 , (5.10)
, (5.10)
где q - характеристическая температура, зависящая от собственной частоты колебания связи в молекуле 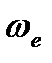
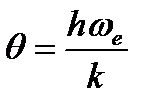
При расчете колебательных составляющих термодинамических функций часто пользуются таблицами Эйнштейна, в которых приводятся значения этих функций в зависимости от величины приведенной характеристической температуры 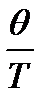 ( [2], табл. 46, с.93).
( [2], табл. 46, с.93).
Значения 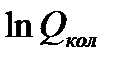 рассчитываются для одного конкретного колебания. Линейная многоатомная молекула, содержащая n атомов, обладает 3n-5 колебательными степенями свободы движения, а нелинейная имеет 3n-6 степеней свободы. Поэтому в многоатомных молекулах колебательные составляющие термодинамических функций, рассчитанные для каждого вида колебательного движения, суммируются.
рассчитываются для одного конкретного колебания. Линейная многоатомная молекула, содержащая n атомов, обладает 3n-5 колебательными степенями свободы движения, а нелинейная имеет 3n-6 степеней свободы. Поэтому в многоатомных молекулах колебательные составляющие термодинамических функций, рассчитанные для каждого вида колебательного движения, суммируются.
При температурах меньше 2000К электронная составляющая суммы по состояниям определяется вырождением невозбужденного основного состояния 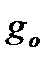 :
:
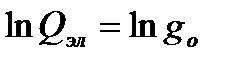 (5.11)
(5.11)
Величина 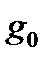 зависит от числа неспаренных электронов, находящихся на молекулярных орбиталях. Если все электроны спарены (синглетное состояние), то
зависит от числа неспаренных электронов, находящихся на молекулярных орбиталях. Если все электроны спарены (синглетное состояние), то 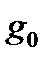 =1 и электронная составляющая не вносит вклад в термодинамические функции.
=1 и электронная составляющая не вносит вклад в термодинамические функции.
Статистическая термодинамика позволяет рассчитать теплоемкость идеального газа при различных температурах. Изобарную молярную теплоемкость можно представить в виде суммы составляющих
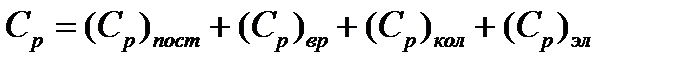 (5.12)
(5.12)
Используя уравнения (6.2) и (6.3), нетрудно показать, что для идеального газа
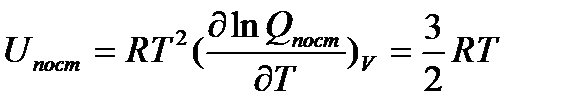 (5.13)
(5.13)
Это выражение совпадает с величиной, полученной в рамках классической механики, согласно которой на одну степень свободы движения приходится энергия равная 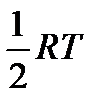 .
.
Изохорная теплоемкость 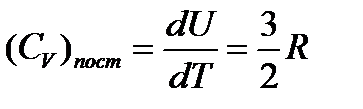 , а изобарная
, а изобарная
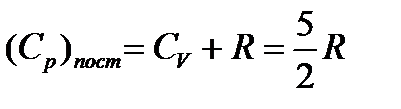 .
.
Для двухатомных и линейных многоатомных молекул
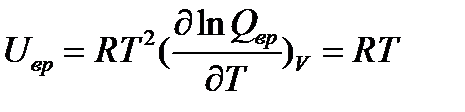 (5.14)
(5.14)
и вращательная составляющая теплоемкости 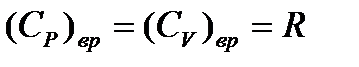 .
.
Для многоатомных несимметричных нелинейных молекул
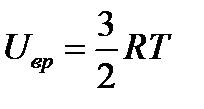 и
и 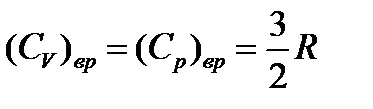 .
.
Значения теплоемкости газа, также как и в случае поступательного движения, соответствует представлениям классической механики, согласно которым на одну степень свободы движения приходится значение теплоемкости равное 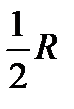 . Вращающиеся линейные молекулы имеют две степени свободы (координаты), а нелинейные молекулы – три степени свободы.
. Вращающиеся линейные молекулы имеют две степени свободы (координаты), а нелинейные молекулы – три степени свободы.
Таким образом, для двухатомной или линейной многоатомной молекулы
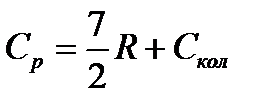 (5.15)
(5.15)
Для нелинейной многоатомной молекулы
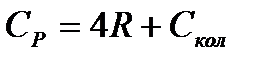 (5.16)
(5.16)
Электронная составляющая теплоемкости 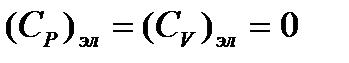 .
.
Следовательно, расчет теплоемкости сводится к нахождению колебательной составляющей для каждого вида колебания.
Пример:. Рассчитать изобарную молярную теплоемкость водорода при Т=298К и 1000К.
Решение:.
Для молекулы водорода волновое число собственных колебаний 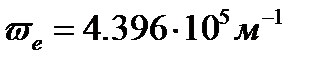 ([2], табл.107, с. 177) и
([2], табл.107, с. 177) и
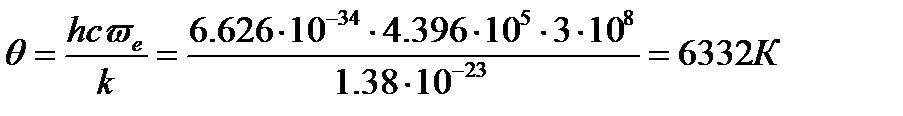
Для нахождения колебательной составляющей теплоемкости воспользуемся таблицами Эйнштейна (КС, табл. 46, с.93).
При 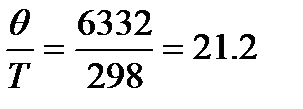
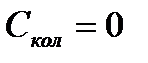 Дж/моль×К
Дж/моль×К
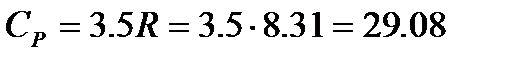 Дж/моль×К
Дж/моль×К
При 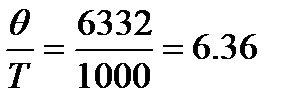
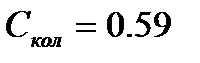 Дж/моль×К и
Дж/моль×К и
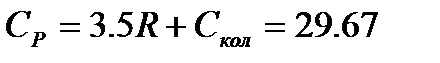 Дж/моль×К .
Дж/моль×К .
Пример:. Рассчитаем изобарную молярную теплоемкость метана при 500К.
Решение:.
Молекула метана – нелинейная многоатомная молекула. В табл. 110, с.187 [2] приведены волновые числа собственных колебаний многоатомных молекул и соответствующие им характеристические температуры. Молекула метана имеет 9 колебательных степеней свободы, причем некоторые колебания вырождены, т.е. характеризуются одним и тем же волновым числом. Следовательно, для метана
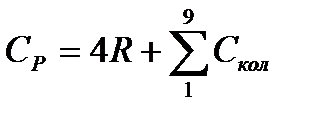
В таблице 5.1 приводятся результаты расчета колебательной составляющей изобарной теплоемкости метана при Т=500К.
Таблица 5.1 – Расчет колебательных составляющих изобарной теплоемкости для молекулы метана
| q | Степень вырождения | 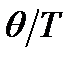
| 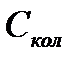
|
| 4196.8 | 8.39 | 0.13 | |
| 4354.1 | 8.71 | 0.11 | |
| 2206.8 | 4.41 | 2.02 | |
| 1879.6 | 3.76 | 2.86 |
Таким образом суммарное значение колебательной составляющей составляет 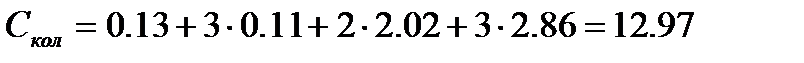 Дж/моль×К и изобарная молярная теплоемкость при 500К
Дж/моль×К и изобарная молярная теплоемкость при 500К 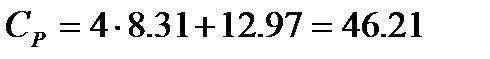 Дж/моль×К .
Дж/моль×К .
Классическая термодинамика позволяет определить теплоемкость газа при различных температурах, используя интерполяционные уравнения:
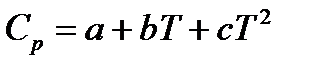 или
или 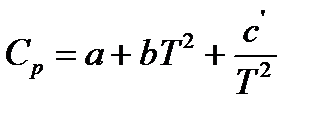 ,
,
при этом коэффициенты 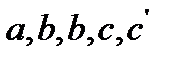 находятся из опытных данных и приводятся в справочниках (например, [2], табл. 44, с.72).
находятся из опытных данных и приводятся в справочниках (например, [2], табл. 44, с.72).
Для метана расчет изобарной теплоемкости по интерполяционному уравнению 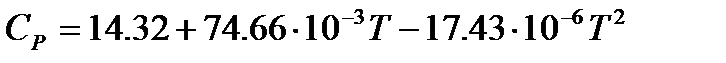 при 500К дает величину
при 500К дает величину 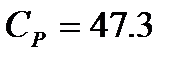 Дж/моль×К.
Дж/моль×К.
5.1 Многовариантное задание № 13 «Расчет теплоемкости идеального газа»
Используя спектральные данные, вычислить теплоемкость идеального газа А при температуре Т (таблица 5.2). Полученный результат сравнить с величиной, рассчитанной с использованием интерполяционных уравнений.
5.2 Контрольные вопросы
1. Что показывает сумма по состояниям? Что такое статистический вес?
2. С какой термодинамической функцией связана сумма по состояниям?
3. Как представить сумму по состояниям в виде составляющих по различным видам движения молекулы?
4. От каких параметров зависит поступательная составляющая суммы по состояниям?
5. От каких молекулярных констант зависит вращательная составляющая суммы по состояниям?
6. С какой молекулярной константой связана характеристическая температура? Для вычисления какой составляющей суммы по состояниям необходимо рассчитывать эту величину?
7. Как рассчитать колебательную составляющую суммы по состояниям для многоатомной молекулы?
8. От чего зависит электронная составляющая суммы по состояниям?
9. Какие термодинамические функции можно рассчитать, используя сумму по состояниям?
10. Какие составляющие термодинамических функций можно определить, используя таблицы Эйнштейна?
11. Как вычислить изобарную молярную теплоемкость газа методом статистической термодинамики?
Таблица 5.2 – Варианты заданий
| Вариант | Вещество А | Температура Т, К | |||||
| Подвариант | |||||||
| CS2 | |||||||
| PCl3 | |||||||
| C2H2 | |||||||
| NO2 | |||||||
| CO2 | |||||||
| H2O | |||||||
| NH3 | |||||||
| SO2 | |||||||
| CCl4 | |||||||
| H2S | |||||||
| N2O | |||||||
| C2H4 | |||||||
| CHCl3 | |||||||
| CH3Cl | |||||||
| NH3 | |||||||
| NО2 | |||||||
| H2O | |||||||
| SO2 | |||||||
| NO | |||||||
| N2O | |||||||
| C2H4 | |||||||
| CS2 | |||||||
| H2S | |||||||
| HCl | |||||||
| CO2 | |||||||
| CO |
Дата добавления: 2021-01-26; просмотров: 878;











