Кинематика поступательного движения материальной точки и твердого тела

Механика – раздел физики, в котором изучается механическое движение, как одно из форм движения материи. В природе существуют четыре основных состояния вещества: газообразное, жидкое, твердое и плазма. Механика в настоящее время включает в себя кинематику и динамику материальной точки, твердого тела, гидродинамику, газодинамику.

В механике вводятся следующие приближения:

1. Тело можно считать материальной точкой в тех задачах, где можно пренебречь физически малым объемом по сравнению с объемом других тел системы.

2. Тело называется абсолютно твердым, если деформацией его можно пренебречь.

Кинематика изучает движение тел, не рассматривая причин, вызывающих это движение. Чтобы описать движение, необходимо указать положение тела в пространстве, т.е. координаты, а также скорость тела в каждый момент времени.

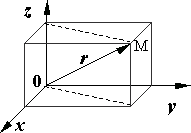
1. Перемещение. Положение материальной точки в пространстве может быть задано с помощью радиус-вектора r, соединяющего начало системы координат с материальной точкой М. (рис. 1.1). Размерность радиус-вектора [r] = м.

Рис. 1.1.

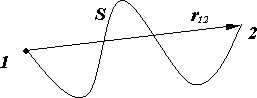
Рис. 1.2.

2. Путь. Линия, которую описывает материальная точка при движении, называется траекторией. Расстояние S между точками 1 и 2, отсчитанное вдоль траектории, называется путем (рис. 1.2).

Вектор 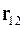, проведенный из точки 1 в точку 2, называется перемещением материальной точки.

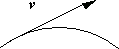3. Скорость. Векторная величина, характеризующая направление движения и быстроту перемещения частицы по траектории, называется скоростью. Вектор скорости направлен по касательной в каждой точке траектории (рис. 1.3). Размерность скорости [n] = м/с.

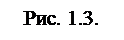Мгновенная скорость n есть производная по времени от радиус-вектора перемещения :

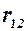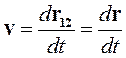. (1.1)

Проекции вектора скорости v на оси декартовой системы координат:

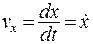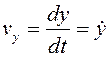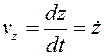, , . (1.2)

В частности, при равномерном движении:

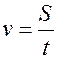. (1.3)

где S – путь.

При неравномерном движении нередко вводят среднюю скорость вдоль осей координат:

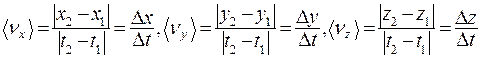(1.4)

Если при движении изменяется направление скорости, то путь S заменяется суммой

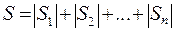, (1.5)

где 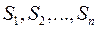- отрезки пути между точками, в которых скорость n обращается в ноль. Средняя путевая скорость при таком движении:

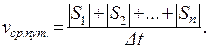(1.6)

где 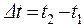- время движения.

4. Ускорение. Мгновенным ускорением называется вектор a, равный первой производной по времени от скорости материальной точки:

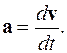(1.7)

Размерность ускорения: [a] = м/с2. Поскольку скорость равна первой производной от вектора перемещения

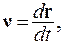(1.8)

то ускорение можно записать

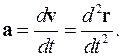(1.9)

Среднее ускорение вдоль осей координат:

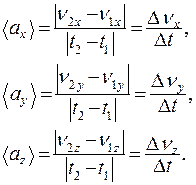(1.10)

При движении по криволинейной траектории вектор a можно разложить на две составляющие:

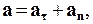(1.11)

где 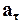– касательное, или тангенциальное ускорение и 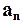- нормальное ускорение, направленное вдоль главной нормали (рис. 1.4).

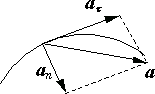
Рис. 1.4.

Сложное движение твердого тела может быть представлено в виде суммы поступательного и вращательного движений. В качестве примера рассмотрим движение шара по вогнутой поверхности.

Шар совершает поступательное, колебательное движения и вращается вокруг собственной оси (рис. 1.5).

Рис. 1.5.

Каждое из этих движений можно рассматривать независимо. Колебательное движение можно рассматривать как часть вращательного движения.

Поступательное движение твердого тела характеризуется тем, что все точки тела движутся с одинаковой по величине и направлению скоростью n. Прямая AB, соединяющая какие-либо две точки тела, при перемещении остается параллельной начальному положению (рис. 1.6).

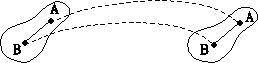
Рис. 1.6.

Для описания поступательного движения твердого тела достаточно рассмотреть движение одной точки. Запишем в векторной форме кинематические уравнения для нахождения пути S, пройденного телом, и скорости тела n в любой момент времени при неравномерном движении с постоянным ускорением a:

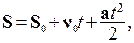
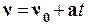(1.12)

где 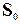– начальное положение тела;

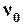– начальная скорость;

a – ускорение тела.

При 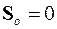находим:

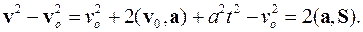(1.13)

При равномерном поступательном движении материальной точки и твердого тела:

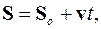
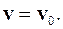(1.14)