Закон сохранения полной механической энергии

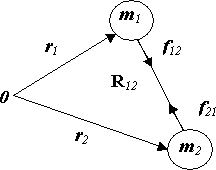Пусть замкнутая система состоит из двух взаимодействующих друг с другом частиц. В соответствии с третьим законом Ньютона:

,

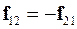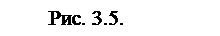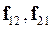где – внутренние силы, действующие на частицу со стороны другой частицы.

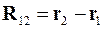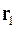Введем вектор , где и 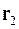- радиус-векторы частиц (рис. 3.5).

Запишем уравнения движения частиц:

,

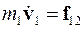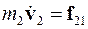. (3.32)

Умножим первое из этих уравнений на 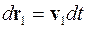, а второе на 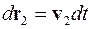и сложим уравнения

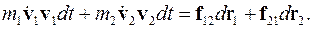(3.33)

Левая часть этого соотношения - приращение кинетической энергии, а правая - приращение работы:

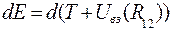
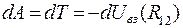
отсюда находим

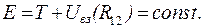(3.34)

Здесь 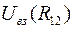называется потенциальной энергией взаимодействия и зависит от расстояния между частицами. Для двух частиц, движущихся со скоростям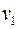и и :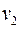

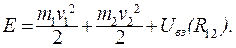(3.35)

Потенциальную энергию взаимодействия 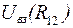в этом случае можно рассматривать как потенциальную энергию U одной частицы, находящейся в поле сил другой частицы.

Рассмотрим теперь систему, состоящую из n частиц, взаимодействующих с силами .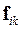

Уравнение движения i-той частицы

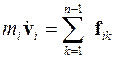. (3.36)

Если на частицу действует внешняя консервативная сила 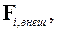тогда уравнение движения примет вид

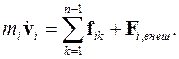(3.37)

Умножим (3.37) на 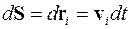и сложим все уравнения, находим

.

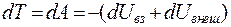отсюда следует, что полная механическая энергия сохраняется

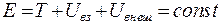(3.38)

Закон сохранения полной механической энергии системы можно сформулировать следующим образом: Полная механическая энергия системы тел, на которые действуют только консервативные силы, остается постоянной.