Закон сохранения импульса

Запишем уравнения движения для всех частиц, взаимодействующих друг с другом с силами 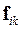, на которые действуют внешние силы F_iвнеш, и сложим эти уравнения

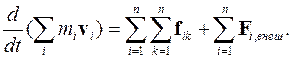(3,39)

Сумма всех внутренних сил равна нулю, поэтому (3.39) примет вид

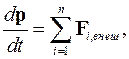(3.40)

где 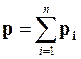- полный импульс системы;

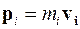- импульс частицы.

Тогда при отсутствии внешних сил

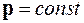. (3.41)

Итак, сформулируем закон сохранения импульса: Импульс замкнутой системы материальных точек остается постоянным.

Импульс системы можно представить в виде произведения суммарной массы системы частиц на скорость центра масс системы.

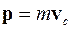. (3.42)

Применение законов сохранения энергии и импульса

Абсолютно упругим называют удар, при котором механическая энергия тел не переходит в немеханические виды энергии (тепловая энергия, энергия деформации тела и др.).

Абсолютно неупругим ударом называют удар, при котором кинетическая энергия полностью или частично превращается во внутреннюю энергию.

Центральным называется соударение шаров, движущихся вдоль прямой, проходящей через их центры.

Неупругий удар

После удара шары слипаются и останавливаются, либо движутся с одинаковой скоростью. При неупругом ударе применяется закон сохранения полного импульса

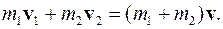(3.43)

Из (3.43) найдем скорость тел после соударения

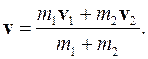(3.44)

Упругий удар

Шары до соударения движутся либо навстречу, либо один шар догоняет другой. Применяются законы сохранения энергии и импульса: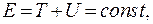

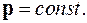
Если потенциальная энергия тел до и после соударения не изменяется, то энергию системы можно считать равной сумме кинетических энергий, а полный импульс равным сумме векторов импульсов отдельных шаров:

До соударения

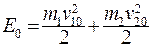(3.45)

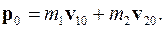
После соударения

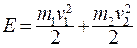(3.46)

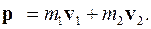
Из закона сохранения энергии следует

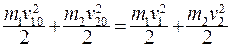(3.47)

Из закона сохранения импульса находим

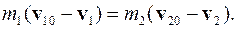(3.48)

Разделим уравнение (3.47) на уравнение (3.48) и запишем в виде

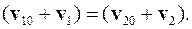(3.49)

Умножим полученное уравнение (3.49) на 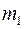и сложим с (3.48):

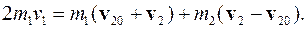
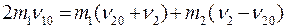
Умножим (3.49) на 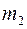и вычтем из (3.48):

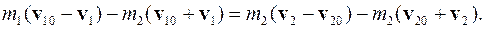
Скорости шаров после соударения:

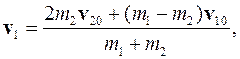
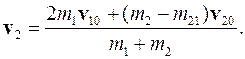(3.50)