Спектральные серии атома водорода.
Исследования спектров излучения разреженных газов (т.е. спектров излучения отдельных атомов) показали, что каждому газу присущ определенный линейчатый спектр, состоящий из отдельных спектральных линий или групп близко расположенных линий. Особенно отчетливо это проявляется в спектре простейшего атома водорода.
Швейцарский ученый И.Бальмер подобрал эмпирическую формулу, описывающую все известные в то время спектральные линии атома водорода в видимой области спектра:
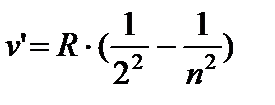 (8.3),
(8.3),
где n=3;4;5;6.
Наряду с серией Бальмера в спектре атомарного водорода были обнаружены другие серии, волновые числа которых можно представить аналогичными формулами.
В ультрафиолетовой области серия Лаймана:
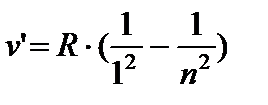 n = 2;3… (8.4)
n = 2;3… (8.4)
В инфракрасной области:
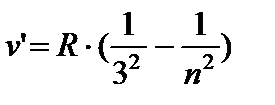 - серия Пашена, n =4;5…
- серия Пашена, n =4;5…
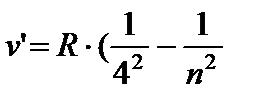 ) - серия Брэкета, n = 5;6… (8.5)
) - серия Брэкета, n = 5;6… (8.5)
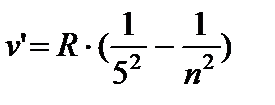 - серия Пфунда, n = 6;7…
- серия Пфунда, n = 6;7…
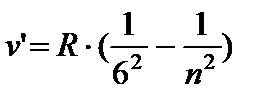 - серия Хемфри, n = 7;8…
- серия Хемфри, n = 7;8…
Анализируя соотношения (8.3) – (8.5), можно сказать, что все серии атомарного водорода можно представить общей формулой, называемой обобщенной формулой Бальмера:
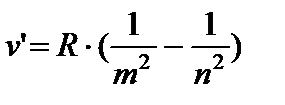 (8.6)
(8.6)
где m имеет в каждой данной серии постоянное значение, m=1;2;3;4;5;6 (определяет серию); а n=m+1, m+2,… (определяет отдельные линии этой серии).
Энергия стационарного состояния атома: 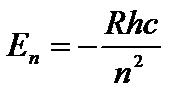 (8.9)
(8.9)
Знак «–» имеет условное значение, чисто физический смысл – энергия электрона в поле положительного ядра отрицательна. Из (8.9) видно, что энергия стационарных состояний образует дискретный ряд при n=1;2;3…
Постулаты, выдвинутые Бором, позволили рассчитать спектр атома водорода и водородоподобных систем (систем, состоящих из ядра с зарядом Ze и одного электрона (например, ионы Не+, Li+), а также теоретически вычислить постоянную Ридберга.
Следуя Бору, рассмотрим движение электрона в водородоподобной системе, ограничиваясь круговыми стационарными орбитами. Потенциальная энергия взаимодействия электрона с ядром:
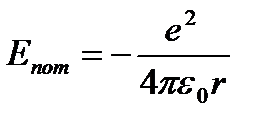 (9.1),
(9.1),
r – радиус орбиты. Кинетическая энергия электрона, движущего вокруг ядра: 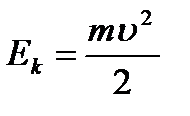 (9.2).
(9.2).
Тогда полная энергия атома:
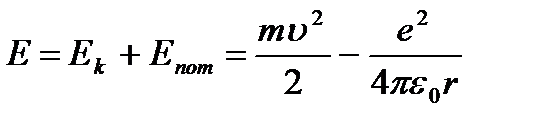 (9.3).
(9.3).
Электрон вокруг ядра движется с ускорением 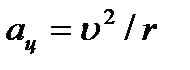 под действием кулоновской силы:
под действием кулоновской силы: 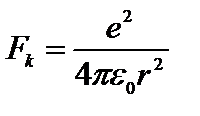 .
.
По второму закону Ньютона (ma = Fk) можно записать:
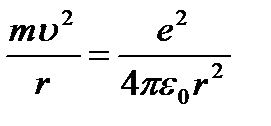 (9.4);
(9.4);
отсюда 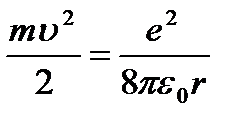 (9.5).
(9.5).
Поставим (9.5) в (9.3): 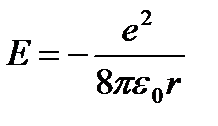 (9.6).
(9.6).
Бор предложил правило отбора или правило квантования (третий постулат Бора): из всех возможных орбит электрона осуществляется только те, для которых момент импульса электрона кратен постоянной Планка:
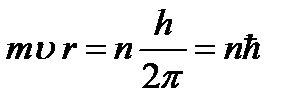 (9.7),
(9.7),
где n=1,2,3,… – главное квантовое число. Используя соотношения (9.4) и (9.7) определим радиус стационарной орбиты электрона:
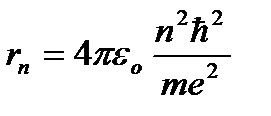
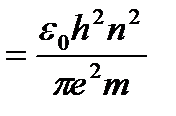 (9.8),
(9.8),
при 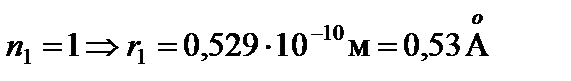 (радиус первой орбиты).
(радиус первой орбиты).
Из (9.8) следует 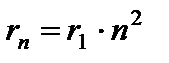 . Подставляя (9.8) в (9.10) получим выражение для энергии стационарных состояний:
. Подставляя (9.8) в (9.10) получим выражение для энергии стационарных состояний:
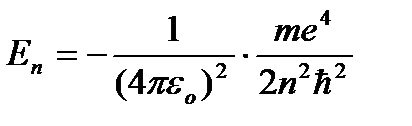 =
= 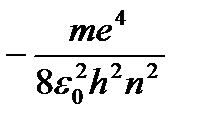 (9.9)
(9.9)
При 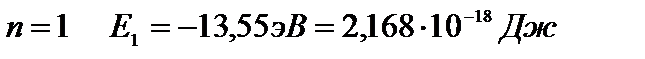 – энергия первого стационарного состояния.
– энергия первого стационарного состояния.
В состоянии с энергией Е1 атом может находиться сколь угодно долго. Для того, чтобы ионизировать атом водорода, т.е. оторвать от него электрон, ему нужно сообщить энергию 13,55 эВ.
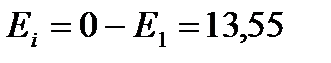 эВ;
эВ; 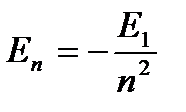 ;
;
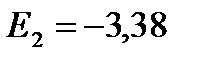 эВ;
эВ; 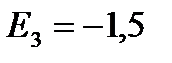 эВ;
эВ; 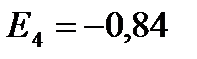 эВ и т.д.
эВ и т.д.
Состояние 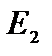 ,
, 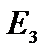 ,… соответствуют возбужденному атому. Время жизни в этих состояниях имеет порядок
,… соответствуют возбужденному атому. Время жизни в этих состояниях имеет порядок 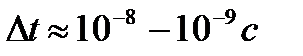 . За это время электрон успевает совершить около 100 млн. оборотов вокруг ядра.
. За это время электрон успевает совершить около 100 млн. оборотов вокруг ядра.
Придавая n различные целочисленные значения, получим для атома водорода, согласно формуле (9.9), возможные уровни энергии. Энергия атома водорода с увеличением п возрастает и энергетические уровни сближаются к границе, соответствующей значению п=¥. Атом водорода обладает, таким образом, минимальной энергией (Е1=–13,55 эВ) при n=1 и максимальной (Е¥=0) при п=¥. Следовательно, значение Е¥=0 соответствуетионизацииатома (отрыву от него электрона). Согласно второму постулату Бора, при переходе атома водорода из стационарного состояния n в стационарное состояние т с меньшей энергией испускается квант:
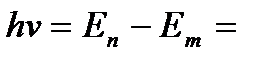
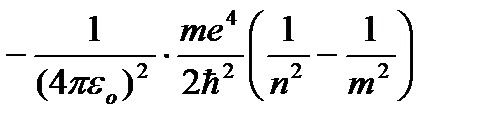 ,
,
откуда частота излучения:
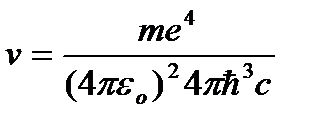
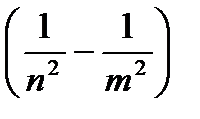 =R
=R 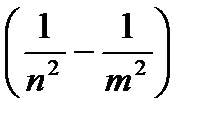 , (9.10)
, (9.10)
где 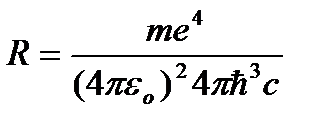 .
.
Воспользовавшись при вычислении R современными значениями универсальных постоянных, получим величину, совпадающую с экспериментальным значением постоянной Ридберга в эмпирических формулах для атома водорода: 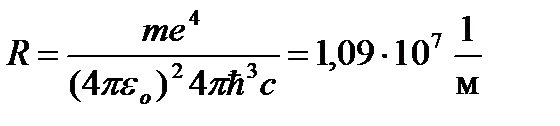 .
.
Это совпадение доказывает правильность полученной Бором формулы для энергетических уровней водородоподобной системы.
Подставляя, например, в формулу (9.10) т=1 и п=2, 3, 4, ..., получим группу линий, образующих серию Лаймана и соответствующих переходам электронов с возбужденных уровней (п=2, 3, 4, ...) на основной (т=1). Аналогично, при подстановке т=2, 3, 4, 5, 10 и соответствующих им значений n получим серии Бальмера, Пашена, Брэкета, Пфунда и Хэмфри (часть из них схематически представлена на рис.9.1.). Следовательно, по теории Бора, количественно объяснившей спектр атома водорода, спектральные серии соответствуют излучению, возникающему в результате перехода атома в данное состояние из возбужденных состояний, расположенных выше данного.
 Теория Бора показала неприменимость классической физики к внутриатомным явлениям и необходимость применения квантовых законов в микромире. Но попытка построить аналогичную теорию для атома гелия потерпела неудачу. Теория Бора не была ни последовательно классической, ни последовательно квантовой теорией. Недостатки теории Бора могли быть устранены путем создания новой квантовой теории, в которой поведение и движение микрочастиц подчиняется своим законам. Это было осуществлено при создании квантовой механики.
Теория Бора показала неприменимость классической физики к внутриатомным явлениям и необходимость применения квантовых законов в микромире. Но попытка построить аналогичную теорию для атома гелия потерпела неудачу. Теория Бора не была ни последовательно классической, ни последовательно квантовой теорией. Недостатки теории Бора могли быть устранены путем создания новой квантовой теории, в которой поведение и движение микрочастиц подчиняется своим законам. Это было осуществлено при создании квантовой механики.
Состояние электрона в атоме характеризуется не одним, а несколькими квантовыми числами.
Первое их квантовых чисел – главное квантовое число: n=1; 2;3,… Оно определяет уровни энергии электрона в атоме: 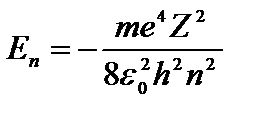 и радиусы стационарных орбит
и радиусы стационарных орбит 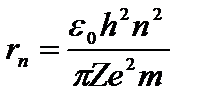 . Эти выражения вытекают из решения уравнения Шредингера и совпадают с соответствующими формулами, полученными Бором.
. Эти выражения вытекают из решения уравнения Шредингера и совпадают с соответствующими формулами, полученными Бором.
Второе квантовое число – орбитальное квантовое число  , которое при данном n может принимать значения 0, 1, 2, ..., n–1 . Это число определяет орбитальный момент импульса
, которое при данном n может принимать значения 0, 1, 2, ..., n–1 . Это число определяет орбитальный момент импульса 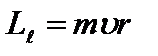 электрона относительно ядра. Момент импульса электрона в атоме квантуется по формуле:
электрона относительно ядра. Момент импульса электрона в атоме квантуется по формуле: 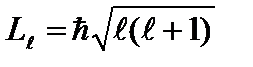
Третье квантовое число – магнитное квантовое число 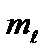 , которое при данном
, которое при данном  принимает значения 0; ±1; ±2,…, ±
принимает значения 0; ±1; ±2,…, ±  ; всего 2
; всего 2  +1 значений. Это число определяет проекции орбитального момента импульса электрона на некоторое произвольно выбранное направление Z. Возможны лишь такие ориентации вектора момента импульса
+1 значений. Это число определяет проекции орбитального момента импульса электрона на некоторое произвольно выбранное направление Z. Возможны лишь такие ориентации вектора момента импульса 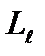 , при которых проекция
, при которых проекция 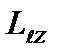 вектора
вектора 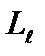 на направление внешнего магнитного поля (ось OZ) принимает значения:
на направление внешнего магнитного поля (ось OZ) принимает значения: 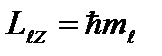
Четвертое квантовое число – спиновое (магнитное спиновое) квантовое число ms. Оно может принимать только два значения 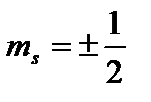 и характеризует возможные значения проекции на ось Z спина (собственного механического момента импульса)
и характеризует возможные значения проекции на ось Z спина (собственного механического момента импульса) 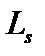 электрона:
электрона: 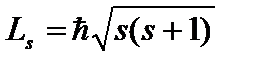 , где
, где 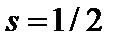 – спиновое квантовое число. Пространственное квантование спина означает, что проекция
– спиновое квантовое число. Пространственное квантование спина означает, что проекция 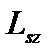 вектора спина
вектора спина 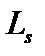 на направление внешнего магнитного поля находится по формуле:
на направление внешнего магнитного поля находится по формуле: 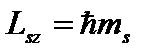 .
.
В 1924 г. швейцарский физик Паули сформулировал принцип, согласно которому: в любом атоме не может быть двух электронов, находящихся в двух одинаковых стационарных состояниях, определяемых набором четырех квантовых чисел – главного n; орбитального  ; магнитного m и спинового ms. Принципу Паули, кроме электронов подчиняются другие частицы, имеющие полуцелый спин (в единицах
; магнитного m и спинового ms. Принципу Паули, кроме электронов подчиняются другие частицы, имеющие полуцелый спин (в единицах 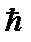 ).
).
Определим число электронов с определенным  .
.
Электроны с  =0 называются s-электронами, их максимальное количество равно
=0 называются s-электронами, их максимальное количество равно 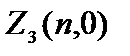 = 2(2×0+1)=2.
= 2(2×0+1)=2.
Электроны с  =1 называются р-электронами, их максимальное количество равно
=1 называются р-электронами, их максимальное количество равно 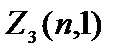 =2(2×1+1)=6.
=2(2×1+1)=6.
Электроны с  =2 называются d-электронами, их максимальное количество равно
=2 называются d-электронами, их максимальное количество равно 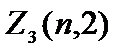 =2(2 2+1)=10.
=2(2 2+1)=10.
Электроны с  =3 называются f-электронами, их максимальное количество равно
=3 называются f-электронами, их максимальное количество равно 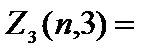 2(2×3+1)=14 и т.д.
2(2×3+1)=14 и т.д.
Максимальное число 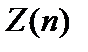 электронов, находящихся в состояниях, определяемых значением n главного квантового числа
электронов, находящихся в состояниях, определяемых значением n главного квантового числа
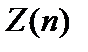 =
= 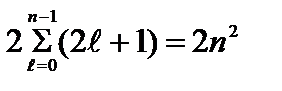
Электроны, занимающие совокупность состояний с одинаковым значением главного квантового числа n, образуют электронную оболочку. Различают следующие электронные оболочки (или слои): К-слой при n = 1; L-слой при n = 2; M-слой при n = 3; N-слой при n =4 и т.д. В каждой квантовой оболочке атома электроны распределяются по подоболочкам, соответствующим определенному значению орбитального квантового числа  ; в зависимости от
; в зависимости от  электрон находится в подгруппе с символами s, p, d, f и т.д.
электрон находится в подгруппе с символами s, p, d, f и т.д.
| Главное квантовое число | Электронная оболочка (слой) | Число электронов в состояниях | Максимальное число электронов | |||
s
(  =0) =0)
| p
(  =1) =1)
| d
(  =2) =2)
| f
(  =3) =3)
| |||
| K | – | – | – | |||
| L | – | – | ||||
| M | – | |||||
| N |
В состоянии, определяемом главным квантовым числом n = 1, могут находиться лишь два s-электрона с двумя различными ориентациями спинов (см.рис.10.1).
Если n = 2, то схема имеет вид, показанный на рис. 10.2.
Последовательность заполнения электронных состояний в атомах химических элементов объясняется принципом Паули.
Этот принцип дает объяснение периодичности свойств химических элементов в периодической системе, созданной Д.И.Менделеевым.
Проследим построение периодической системы (или заполнение электронами слоев атома), которые подчиняются двум принципам: а) заполнение начинается с наименьшей энергии (наиболее устойчивое состояние); б) принцип запрета Паули.
Первый элемент в таблице Менделеева – атом водорода Н, для него Z = 1. Он имеет один электрон, квантовые числа для которого: n =1,  = 0, mе = 0, ms = +1/2 или –1/2, т. е. электронная конфигурация атома водорода: 1S1.
= 0, mе = 0, ms = +1/2 или –1/2, т. е. электронная конфигурация атома водорода: 1S1.
У следующего элемента гелия Не имеются два электрона, квантовые числа: n =1,  = 0, mе = 0, ms = ±1/2, т. е. электронная конфигурация атома гелия: 1S2. Слой К с числом электронов N = 2 заполнен полностью.
= 0, mе = 0, ms = ±1/2, т. е. электронная конфигурация атома гелия: 1S2. Слой К с числом электронов N = 2 заполнен полностью.
Третий элемент литий Li. Его третий электрон имеет квантовые числа: n = 2,  = 0, mе = 0, ms = +1/2 или – 1/2, т. е. электронная конфигурация атома 1S2 2S1.
= 0, mе = 0, ms = +1/2 или – 1/2, т. е. электронная конфигурация атома 1S2 2S1.
У берилия Ве: Z = 4 электронная конфигурация атома 1S2 2S2.
У последующих шести элементов происходит заполнение оболочек 2р. В результате у неона Nе с Z = 10 электронная конфигурация атома 1S2 2S2 2Р6, т.е. L – слой полностью заполнен и на этом заканчивается второй слой периодической таблицы. Не, Nе, а также другие атомы, в которых s- или s- и p-подгруппы полностью заняты электронами, по свойствам аналогичны и химически инертны.
| Z | символ элемента | Название элемента | Электронная конфигурация |
| Н | водород | 1s1 | |
| Не | гелий | 1s2 | |
| Li | литий | 1s1 2s1 | |
| Be | бериллий | 1s22s2 | |
| B | бор | 1s22s22p1 | |
| C | углерод | 1s22s22p2 | |
| N | азот | 1s22s22p3 | |
| O | кислород | 1s22s22p4 | |
| F | фтор | 1s22s22p5 | |
| Ne | неон | 1s22s22p6 | |
| Na | натрий | 1s22s22p63s1 | |
| Mg | магний | 1s22s22p63s2 | |
| Al | алюминий | 1s22s22p63s23р1 | |
| Si | кремний | 1s22s22p63s23р2 | |
| Р | фосфор | 1s22s22p63s23р3 | |
| S | сера | 1s22s22p63s23р4 | |
| Cl | хлор | 1s22s22p63s23р5 | |
| Ar | аргон | 1s22s22p63s23р6 |
Нарушения при заполнении слоев наблюдаются у элемента с Z=19 (калий К), где начинается заполнение оболочки 4s при незаполненной 3d:
| К | калий | 1s22s22p63s23р64s1 | |
| Сa | кальций | 1s22s22p63s23р64s2 | |
| Sc | скандий | 1s22s22p63s23р63d14s2 | |
| Ti | титан | 1s22s22p63s23р63d24s2 |
и т.д., пока не будет заполнена 3d-оболочка.
Это нарушение связано с взаимодействием между электронами, состояние которых характеризуется главными квантовыми числами n=3, n=4 и т.д. В результате взаимодействия возникает такое положение, что состояние с большим n, но малым  может быть энергетически более выгодным.
может быть энергетически более выгодным.
Аналогичная ситуация наблюдается у редкоземельных элементов, или лантаноидов (атомов с номерами 58-71), у которых заполнены оболочки 5s, 5р, 6s при незаполненной 4f оболочке. У них у всех внешняя оболочка 6s2. Еще одно отступление относится к актиноидам (атомов с номерами 90-103), у которых заполняются 5f оболочкапосле заполнения внешней оболочки 7s2.
Тема 29. Оптические квантовые генераторы
В силу правил отбора у атомов многих элементов имеются энергетические уровни, с которых электрон не может непосредственно перейти на более низкий уровень. Эти уровни называются метастабильными состояниями. Электрон может перейти на такой уровень при соударениях с другим электроном или при переходе с более высокого уровня. Продолжительность пребывания электрона в метастабильном состоянии имеет порядок 10-–3 с, в то время как в возбужденном состоянии – 10–8 с.
Излучение, испускаемое при самопроизвольном переходе атома из возбужденного состояния в основное, называется спонтанным излучением. Спонтанное излучение различных атомов происходит не когерентно, т.к. каждый атом начинает и заканчивает излучение независимо от других (рис.15.1а).
Излучение энергии атомом, при котором переход из метастабильного состояния в основное вызывается электромагнитным излучением соответствующей частоты называется вынужденным, или индуцированным, излучением (рис.15.1б).
Вероятность индуцированного излучения резко возрастает при совпадении частоты электромагнитного поля с собственной частотой излучения возбужденного атома. Вынужденное излучение имеет такую же частоту, фазу, поляризацию и направление распространения, как и вынуждающее излучение. Следовательно, вынужденное излучение строго когерентно с вынуждающим излучением, то есть испущенный фотон неотличим от фотона, падающего на атом. Испущенные фотоны, двигаясь в одном направлении и встречая другие возбужденные атомы, стимулируют дальнейшие индуцированные переходы, и число фотонов растет лавинообразно.
Однако наряду с вынужденным излучением возможен и конкурирующий процесс – поглощение. В системе атомов, находящейся в термодинамическом равновесии, поглощение падающего излучения будет преобладать над вынужденным, т.е. падающее излучение при прохождении через вещество будет ослабляться.
Чтобы среда усиливала падающее на нее излучение, необходимо создать неравновесное состояние системы, при котором число атомов в возбужденных состояниях было бы больше, чем их число в основном состоянии. Такие состояния называются состояниями с инверсной заселенностью. Процесс создания неравновесного состоянии вещества (перевод системы в состояние с инверсией населенностей) называется накачкой. Накачку можно осуществить оптическими, электрическими и другими способами. Среды с инверсными состояниями называются активными. Их можно рассматривать в качестве сред с отрицательным коэффициентом поглощения, т.к. падающий пучок света при прохождении через эти среды будет усиливаться.
Впервые на возможность получения сред, в которых свет может усиливаться за счет вынужденного излучения, указал в 1939 г. российский физик В.А.Фабрикант. Он экспериментально обнаружил вынужденное излучение паров ртути, возбужденных при электрическом разряде. Открытие явления усиления электромагнитных волн и изобретенный способ их усиления (В.А.Фабрикант, М.М.Вудынский, Ф.А.Бутаева; 1951) легли в основу квантовой электроники, положения которой позволили впоследствии осуществить квантовые усилители и квантовые генераторы света.
Практически инверсное состояние среды осуществлено в оптических квантовых генераторах, или лазерах (от первых букв английского названия Light Amplification by Stimulated Emission of Radiation – усиление света с помощью вынужденного излучения). Лазеры генерируют в видимой, инфракрасной и ближней ультрафиолетовой областях (в оптическом диапазоне). Идея качественно нового принципа усиления и генерации электромагнитных волн, примененная в мазерах (генераторы и усилители, работающие в сантиметровом диапазоне радиоволн) и лазерах, принадлежит российским ученым Н.Г.Басову и А.М.Прохорову и американскому физику Ч. Таунсу, удостоенным Нобелевской премии 1964 г.
Важнейшими из существующих типов лазеров являются твердотельные, газовые, полупроводниковые и жидкостные (в основу такого деления положен тип активной среды). Более точная классификация учитывает также и методы накачки — оптические, тепловые, химические, электроионизационные и др. Кроме того, необходимо принимать во внимание и режим генерации – непрерывный или импульсный.
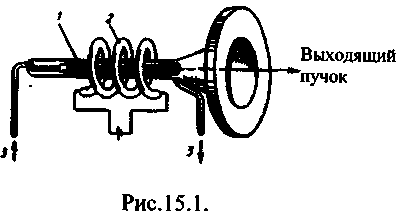 Лазер обязательно имеет три основных компонента: 1) активную среду, в которой создаются состояния с инверсией населенностей; 2) систему накачки (устройство для создания инверсий в активной среде); 3) оптический резонатор (устройство, выделяющее в пространство избирательное направление пучка фотонов и формирующее выходящий световой пучок).
Лазер обязательно имеет три основных компонента: 1) активную среду, в которой создаются состояния с инверсией населенностей; 2) систему накачки (устройство для создания инверсий в активной среде); 3) оптический резонатор (устройство, выделяющее в пространство избирательное направление пучка фотонов и формирующее выходящий световой пучок).
Первым твердотельным лазером, работающим в видимой области спектра (длина волны излучения 0,6943 мкм), был рубиновый лазер, созданный в 1960 г. (Т.Мейман, США). На рис.16.1 представлена схема рубинового лазера. В нем инверсная населенность уровней осуществляется по трехуровневой схеме, предложенной в 1955 г. Н. Г. Басовым и А. М. Прохоровым. Кристалл рубина представляет собой оксид алюминия А12Оз, в кристаллической решетке которого некоторые из атомов А1 замещены трехвалентными ионами Сгэ+ (0,03 и 0,05% ионов хрома соответственно дня розового и красного рубина). Для оптической накачки используется импульсная газоразрядная лампа (2), спирально закрученная вокруг рубинового стержня (1). При интенсивном облучении рубина светом мощной импульсной лампы атомы хрома переходят с нижнего уровня на уровни широкой полосы 3 (рис. 16.2). Так как время жизни атомов хрома в возбужденных состояниях мало (меньше 10-7 с), то осуществляются либо спонтанные переходы 3®1(они незначительны), либо наиболее вероятные безызлучательные переходы на уровень 2 (он называется метастабильным) с передачей избытка энергии решетке кристалла рубина. Переход 2®1 запрещен правилами отбора, поэтому длительность возбужденного состояния 2 атомов хрома порядка 10-3 с, т.е. примерно на четыре порядка больше, чем для состояния 3. Это приводит к «накоплению» атомов хрома на уровне 2. При достаточной мощности накачки их концентрация на уровне 2 будет гораздо больше, чем на уровне 1, т. е. возникает среда с инверсной населенностью уровня 2.
Рубиновый стержень лазера представлял собой цилиндр, торцы которого были тщательно отполированы и покрыты слоем серебра таким образом, что один торец полностью отражал свет, а другой – частично отражал и частично пропускал свет. При вспышке лампы накачки в рубиновый стержень попадают фотоны различных частот. Атомы хрома, поглотив часть фотонов определенной энергии, переходят в возбужденное состояние. За счет ограниченных спонтанных переходов в стержне может возникнуть вынужденное излучение, распространяющееся строго вдоль его оси и усиливающееся при многократных отражениях от торцовых зеркал, которые выполняют роль объемного резонатора. В результате возникает мощное монохроматическое излучение – световой импульс, часть которого выходит через полупрозрачное зеркало. Длительность такого импульса 10–3 с. Это связано с тем, что все возбужденные ионы хрома за это время переходят в невозбужденное состояние. Световой луч лазера строго направлен и обладает малой расходимостью. Объемный резонатор лазера служит для создания положительной обратной связи и для формирования геометрических параметров выходного луча лазера.
Не вся энергия, поглощенная рубиновым стержнем, превращается в лазерное излучение. Часть ее, довольно значительная (»50%), тратится на нагревание стержня, поэтому в конструкции лазера предусмотрено охлаждение 3. При температуре стержня порядка 1000 К рубиновый лазер разрушается.
Существует большое количество лазерных материалов: стекло, в которое введены ионы неодима, флюорит кальция с иона ми самария и др. Они дают световое излучение различных длин волн: рубиновый лазер – 0,694 мкм, лазер на стекле с неодимом – 1,06 мкм (инфракрасное излучение). В лазерах в качестве активной среды могут быть использованы газы или смеси газов (Ne, Ar, Ne–Не, СО2 и др.). В газовых лазерах атомы активной среды часто возбуждают высокочастотным разрядом. Как правило, излучение газовых лазеров непрерывно. Созданы полупроводниковые, химические, газодинамические и другие лазеры.
Лазерное излучение обладает следующими свойствами:
1) временная и пространственная когерентность;
2) строгая монохроматичность;
3) большая плотность потока энергии;
4) очень малое угловое расхождение в пучке.
Необычные свойства лазерного излучения нашли широкое применение. Например, в светолучевых станках с помощью лазерного луча делают отверстия в часовых камнях из рубина, алмаза, в тугоплавких сплавах и труднообрабатываемых металлах. В микроэлектронике с помощью лазеров производят сварку различных соединений для микросхем, напыляют полупроводниковые слои и т.д.
Тема 30. Элементы квантовой механики
Французский ученый Луи де Бройль, развивая представления о двойственной корпускулярно-волновой природе света, выдвинул в 1923 году гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что между свойствами света и свойствами материальных частиц существует глубокая аналогия, следовательно материальные частицы обладают также двойственной природой, т.е. в определенных условиях проявляются их волновые свойства.
 Де-Бройль постулировал, что частице с импульсом
Де-Бройль постулировал, что частице с импульсом 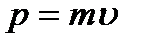 соответствует длина волны:
соответствует длина волны: 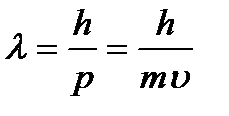 (1.2)
(1.2)
Это соотношение (формула де Бройля) справедливо для любой частицы с импульсом р.
Вскоре гипотеза де Бройля была подтверждена экспериментально. Американские физики К.Дэвиссон и Л.Джермер в 1927 г. изучали рассеяние электронов на монокристалле никеля с помощью установки, изображенной на рис. Пучок электронов из электронной пушки 1 направлялся на кристалл никеля 2, рассеянные от кристалла электроны 3 улавливались специальным приемником 4, соединенным с чувствительным гальванометром. Интенсивность отраженного пучка определялась по силе тока, текущего через гальванометр. Опыты показали, что при заданном угле падения электроны отражаются от поверхности кристалла под различными углами, причем в одних направлениях наблюдаются максимумы числа отраженных электронов, в других – минимумы, то есть наблюдалась дифракционная картина. Это явление наблюдалось, когда длина электронной волны де Бройля 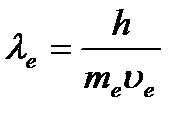 имеет порядок межатомного расстояния в кристалле. Дифракционные максимумы соответствовали формуле Вульфа-Брэггов
имеет порядок межатомного расстояния в кристалле. Дифракционные максимумы соответствовали формуле Вульфа-Брэггов 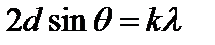 , а брэгговская длина волны оказалась в точности равной длине волны, вычисленной по формуле (1.2).
, а брэгговская длина волны оказалась в точности равной длине волны, вычисленной по формуле (1.2).
Позже П.С.Тартаковский и Г.Томсон исследовали прохождение быстрых электронов через тонкие металлические пленки. При этом на фотопластинках за этими пленками получалась дифракционная картина такая же, как при дифракции рентгеновских лучей на поликристаллах.
В 1849 г. В.А.Фабрикант, Л.М.Биберман и Н.Г.Сушкин осуществили опыты по дифракции электронов с очень малой силой тока в приборе, то есть каждый электрон регистрировался фотопластинкой в случайных местах. При длительной экспозиции была получена такая же дифракционная картина, как и при короткой с большой силой тока. Это означает, что волновые свойства присущи каждому электрону в отдельности, однако дифракция одного электрона не дает всей системы точек, которая получается при дифракции от потока. След одного электрона окажется лишь в одной точке, которая разрешена условием дифракции. В этом проявляется корпускулярная природа электронов, так как электрон не может расплыться. В какое именно из мест попадет электрон, говорить нельзя. Можно говорить лишь о вероятности попадания в точку пространства.
Таким образом, электрону присуща двойственная природа, т.е. он сочетает в себе свойства и частицы, и волны. Волновая природа электронов подтверждается опытами по их дифракции. Корпускулярная природа электронов проявляется в том, что электрон действует как единое целое, не дробясь на части.
Впоследствии дифракционные явления обнаружили также для нейтронов, протонов, атомных и молекулярных пучков. Это окончательно послужило доказательством наличия волновых свойств микрочастиц и позволило описать движение микрочастиц в виде волнового процесса, характеризующегося определенной длиной волны, рассчитываемой по формуле де Бройля (1.2).
Дата добавления: 2016-10-26; просмотров: 8957;











