Энергия гармонических колебаний.

Характерной чертой гармонического осциллятора является то, что средние значения кинетической и потенциальной энергии осциллятора равны друг другу и каждое из них составляет половину полной энергии.

Кинетическую энергия колеблющегося тела можно определить, если в выражение для кинетической энергии 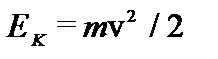подставить скорость :

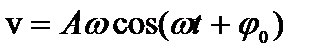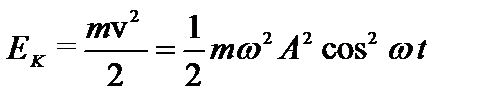(1).

Потенциальная энергия, обусловленная упругой силой, определяется как эквивалент работы, необходимой для смещения тела на расстояние x от положения равновесия, и равна:

.

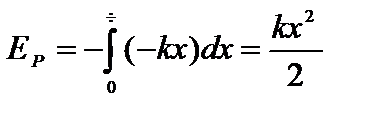
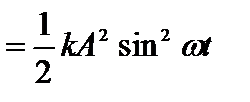Учитывая, что 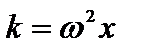, получим:

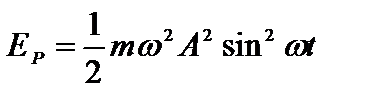. (2).

Полная механическая энергия осциллятора равна: .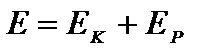

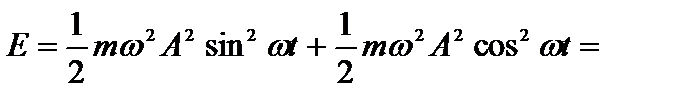
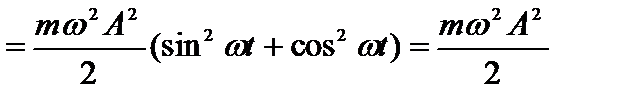
Из выражений (1) и (2) видно, что кинетическая и потенциальная энергии изменяются со временем, причем, когда кинетическая энергия максимальна, потенциальная энергия обращается в нуль, и наоборот (рис.23.1). Период колебания кинетической и потенциальной энергий вдвое меньше периода колебаний системы. Полная механическая энергия гармонического колебания постоянна и пропорциональна квадрату амплитуды и квадрату частоты. Постоянство полной механической энергии обусловлено отсутствием потерь энергии на совершение работы против сил сопротивления.

Тема 19. Затухающие и вынужденные колебания. Сложение колебаний

Реально свободные колебания под действием сил сопротивления всегда затухают. Объясняется это действием сил, тормозящих движение, например, сил трения в месте подвеса при колебаниях маятника, или силой сопротивления среды. В этом случае энергия механических колебаний постепенно расходуется на работу против этих сил. Поэтому свободные колебания под действием сил сопротивления всегда затухают.

Пусть точка совершает линейное гармоническое колебание в вязкой среде. Из опыта известно, что сила сопротивления среды зависит от скорости и направлена в сторону, противоположную скорости. При малых скоростях: 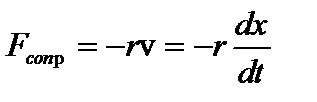, где r – постоянная величина, называемая коэффициентом сопротивления среды. Уравнение колебаний: .

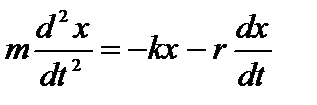Введем обозначения: 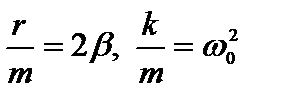, тогда дифференциальное уравнение затухающего колебания:

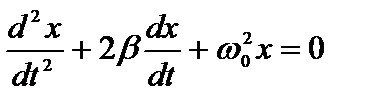(1)

где 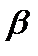– коэффициент затухания, w₀ – собственная частота колебания. При отсутствии трения 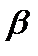=0, уравнение примет вид уравнения для свободных незатухающих колебаний. В результате решения уравнения (1) получим зависимость смещения х от времени, то есть уравнение затухающего колебательного движения: 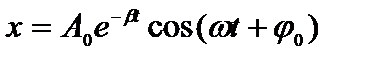(2)

Выражение 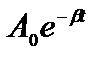называется амплитудой затухающего колебания. Амплитуда уменьшается с течением времени и тем быстрее, чем больше коэффициент затухания. Огибающая на графике зависит от 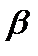. Чем она больше, тем круче огибающая, то есть колебания быстрее затухают (рис.24.1).

Путем подстановки функции (2) и ее производных по времени в уравнение (1), можно найти значение угловой частоты: 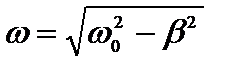. Период затухающих колебаний равен: .

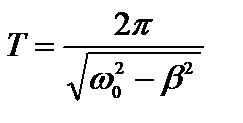Наглядной характеристикой затухания является отношение значений двух амплитуд, соответствующих промежутку времени в один период. Это отношение называют декрементом затухания : .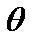

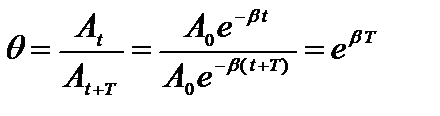Его натуральный логарифм есть безразмерная величина, называемая логарифмическим декрементом затухания: .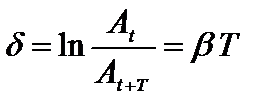

Промежуток времени 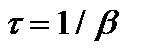, в течение которого амплитуда затухающего колебания убывает в е раз, называют временем релаксации.

Тогда выражение для логарифмического декремента затухания примет вид: 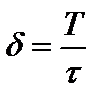или .

Логарифмический декремент затухания – величина, обратная числу колебаний N, по истечении которых амплитуда колебаний уменьшается в е раз.