Соотношение неопределенностей Гейзенберга.

Подтвержденная экспериментально гипотеза де Бройля о корпускулярно-волновом дуализме свойств вещества коренным образом изменила представления о свойствах микрообъектов. Всем микрообъектам присущи и корпускулярные, и волновые свойства; в то же время любую из микрочастиц нельзя считать ни частицей, ни волной в классическом понимании.

В.Гейзенберг, учитывая волновые свойства микрочастиц и связанные с волновыми свойствами ограничения в их поведении, пришел в 1927 г. к выводу, что объект микромира невозможно одновременно с любой наперед заданной точностью харак­теризовать и координатой и импульсом. Согласносоотношению неопределенностей Гейзенберга, микрочастица не может иметь одновременно и определен­ную координату (х, у, z), и определенную соответствующую проекцию импульса (р_х, р_у, p_z), причем неопределенности этих величин удовлетворяют условиям: 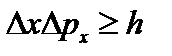, , 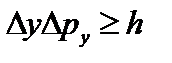, 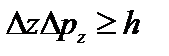(2.1)

где Dx, Dу, Dz – неопределенности координат частицы, а 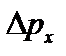, , 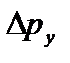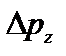- неопределенность компоненты импульса. Произведение неопределенностей координаты и соответствующей ей проекции импульса не может быть меньше величины порядка h. То есть,чем точнее мы знаем координату, тем менее определена проекция импульса и наоборот. Отсюда вытекает и фактическая невозможность одновременно с любой, наперед заданной точностью измерить координату и импульс микрообъекта.

Соотношение неопределенностей получено при одновременном использовании классических характеристик движения частицы (координаты, импульса) и наличия у нее волновых свойств. Оно является квантовым ограничением применимости классической механики к микрообъектам и позво­ляет оценить, например, в какой мере можно применять понятия классической меха­ники к микрочастицам, в частности, с какой степенью точности можно говорить о траекториях микрочастиц. Известно, что движение по траектории характеризуется в любой момент времени определенными значениями координат и скорости. Выразим соотношение неопределенностей (2.1) в виде

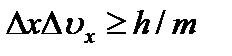(2.4)

Из этого выражения следует, что чем больше масса частицы, тем меньше неопределен­ности ее координаты и скорости и, следовательно, с тем большей точностью можно применять к этой частице понятие траектории. Для описания движения макротел с абсолютной достоверностью можно пользоваться законами классической механики, чего нельзя делать для описания, например, движе­ния электрона в атоме.

В квантовой теории рассматривается также соотношение неопределенностей для энергии Е и времени t, т.е. неопределенности этих величин удовлетворяют условию

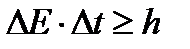(4.5)

где DЕ – неопределенность энергии некоторого состояния системы, Dt – промежуток времени, в течение которого оно существует. Следовательно, систе­ма, имеющая среднее время жизни Dt, не может быть охарактеризована определенным значением энергии; разброс энергии DЕ=h/Dt возрастает с уменьшением среднего времени жизни.