Практическое применение электромагнитной индукции
Явление электромагнитной индукции используется, прежде всего, для преобразования механической энергии в энергию электрического тока. Для этой цели применяются генераторы переменного тока (индукционные генераторы).
| N |
| S |
| ~ |
| ww |
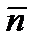
|
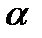
|
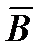
|
| Рис. 4.5 |
| . |
| cos |
| a |
| BS |
| Ф |
| = |
При равномерном вращении рамки угол поворота 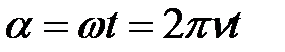 , где
, где 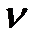 – частота вращения. Тогда
– частота вращения. Тогда
| . |
| cos |
| t |
| BS |
| Ф |
| w |
| = |
По закону электромагнитной индукции ЭДС, наводимая в рамке при
ее вращении,
| . |
| sin |
| sin |
| max |
| t |
| t |
| BS |
| Ф |
| i |
| w |
| e |
| w |
| w |
| e |
| = |
| = |
| ¢ |
| - |
| = |
Если к зажимам рамки с помощью щеточно-контактного аппарата подключить нагрузку (потребителя электроэнергии), то через нее потечет переменный ток.
| + |
| - |
| А |
| В |
| С |
| Т |
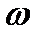
|
| Ф |
| Рис. 4.6 |
обмотку возбуждения через щеточно-контактный аппарат, намагничивает ротор, и при этом образуется электромагнит с северным и южным полюсами.
На статоре генератора расположены три обмотки переменного тока, которые смещены одна относительно другой на 1200 и соединены между собой по определенной схеме включения.
При вращении возбужденного ротора с помощью паровой или гидравлической турбины его полюсы проходят под обмотками статора, и в них индуцируется изменяющаяся по гармоническому закону электродвижущая сила. Далее генератор по определенной схеме электрической сети соединяется с узлами потребления электроэнергии.
Если передавать электроэнергию от генераторов станций к потребителям по линиям электропередачи непосредственно (на генераторном напряжении, которое относительно невелико), то в сети будут происходить большие потери энергии и напряжения (обратите внимание на соотношения 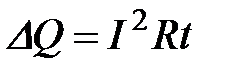 ,
, 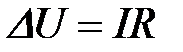 ). Следовательно, для экономичной транспортировки электроэнергии необходимо уменьшить силу тока. Однако, так как передаваемая мощность при этом остается неизменной, напряжение должно
). Следовательно, для экономичной транспортировки электроэнергии необходимо уменьшить силу тока. Однако, так как передаваемая мощность при этом остается неизменной, напряжение должно
увеличиться во столько же раз, во сколько раз уменьшается сила тока.
У потребителя электроэнергии, в свою очередь, напряжение необходимо понизить до требуемого уровня. Электрические аппараты, в которых напряжение увеличивается или уменьшается в заданное количество раз, называются трансформаторами. Работа трансформатора также основана на законе электромагнитной индукции.
| t |
| Ф |
| Ф |
| m |
| w |
| cos |
| = |
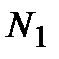
|
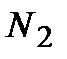
|
| Ф |
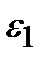
|
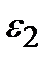
|
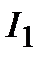
|
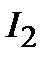
|
| Рис. 4.7 |
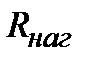
|
| , |
| sin |
| sin |
| t |
| N |
| t |
| Ф |
| N |
| Ф |
| N |
| m |
| m |
| w |
| e |
| w |
| w |
| e |
| = |
| = |
| ¢ |
| - |
| = |
| . |
| sin |
| sin |
| t |
| N |
| t |
| Ф |
| N |
| Ф |
| N |
| m |
| m |
| w |
| e |
| w |
| w |
| e |
| = |
| = |
| ¢ |
| - |
| = |
Тогда 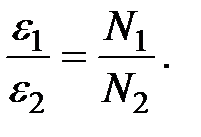
У мощных трансформаторов сопротивления катушек очень малы,
поэтому напряжения на зажимах первичной и вторичной обмоток приблизительно равны ЭДС:
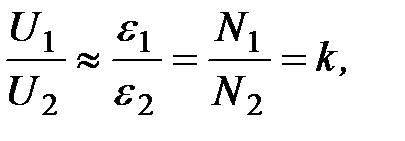
где k – коэффициент трансформации. При k<1 ( 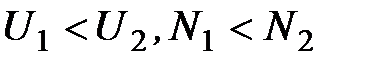 ) трансформатор является повышающим, при k>1 (
) трансформатор является повышающим, при k>1 ( 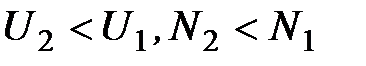 ) трансформатор является понижающим.
) трансформатор является понижающим.
При подключении к вторичной обмотке трансформатора нагрузки, в ней потечет ток 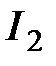 . При увеличении потребления электроэнергии по закону
. При увеличении потребления электроэнергии по закону
сохранения энергии должна увеличиться энергия, отдаваемая генераторами станции, то есть
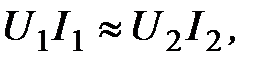
откуда
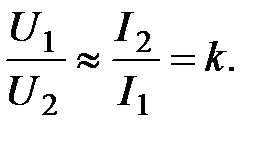
Это означает, что, повышая с помощью трансформатора напряжение
в k раз, удается во столько же раз уменьшить силу тока в цепи (при этом джоулевы потери уменьшаются в k2 раз).
Тема 17. Основы теории Максвелла для электромагнитного поля. Электромагнитные волны
В 60-х гг. XIX в. английский ученый Дж. Максвелл (1831-1879) обобщил экспериментально установленные законы электрического и магнитного полей и создал законченную единую теорию электромагнитного поля. Она позволяет решить основную задачу электродинамики: найти характеристики электромагнитного поля заданной системы электрических зарядов и токов.
Максвелл выдвинул гипотезу, что всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле 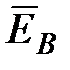 , циркуляция которого и является причиной возникновения ЭДС электромагнитной индукции в контуре:
, циркуляция которого и является причиной возникновения ЭДС электромагнитной индукции в контуре:
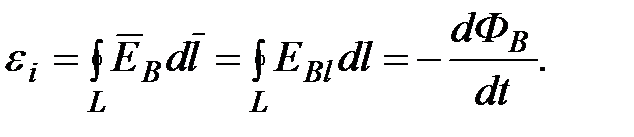 (5.1)
(5.1)
Уравнение (5.1) называют вторым уравнением Максвелла. Смысл этого уравнения заключается в том, что изменяющееся магнитное поле порождает вихревое электрическое, а последнее в свою очередь вызывает в окружающем диэлектрике или вакууме изменяющееся магнитное поле. Поскольку магнитное поле создается электрическим током, то, согласно Максвеллу, вихревое электрическое поле следует рассматривать как некоторый ток,
который протекает как в диэлектрике, так и в вакууме. Максвелл назвал этот ток током смещения.
Ток смещения, как это следует из теории Максвелла
и опытов Эйхенвальда, создает такое же магнитное поле, как и ток проводимости.
В своей теории Максвелл ввел понятие полного тока, равного сумме
токов проводимости и смещения. Следовательно, плотность полного тока
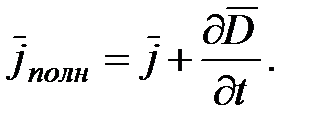
По Максвеллу полный ток в цепи всегда замкнут, то есть на концах проводников обрывается лишь ток проводимости, а в диэлектрике (вакууме) между концами проводника имеется ток смещения, который замыкает ток проводимости.
Введя понятие полного тока, Максвелл обобщил теорему о циркуляции вектора 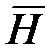 (или
(или 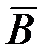 ):
):
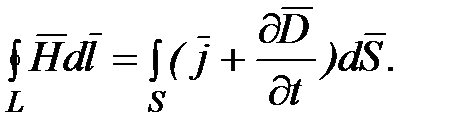 (5.6)
(5.6)
Уравнение (5.6) называется первым уравнением Максвелла в интегральной форме. Оно представляет собой обобщенный закон полного тока и выражает основное положение электромагнитной теории: токи смещения создают такие же магнитные поля, как и токи проводимости.
Созданная Максвеллом единая макроскопическая теория электромагнитного поля позволила с единой точки зрения не только объяснить электрические и магнитные явления, но предсказать новые, существование которых было впоследствии подтверждено на практике (например, открытие электромагнитных волн).
Обобщая рассмотренные выше положения, приведем уравнения, составляющие основу электромагнитной теории Максвелла.
1. Теорема о циркуляции вектора напряженности магнитного поля:
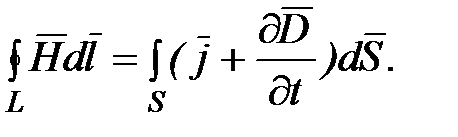
Это уравнение показывает, что магнитные поля могут создаваться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.
2. Электрическое поле может быть как потенциальным ( 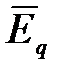 ), так и вихревым (
), так и вихревым ( 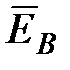 ), поэтому напряженность суммарного поля
), поэтому напряженность суммарного поля 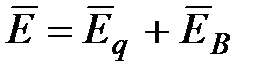 . Так как циркуляция вектора
. Так как циркуляция вектора 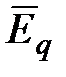 равна нулю, то циркуляция вектора напряженности суммарного электрического поля
равна нулю, то циркуляция вектора напряженности суммарного электрического поля
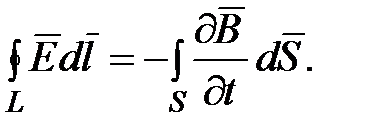
Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и меняющиеся во времени магнитные поля.
3. 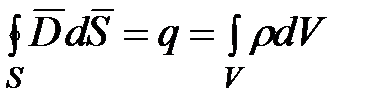 ,
,
4. 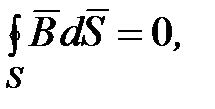
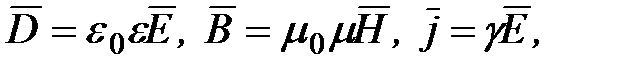
где 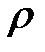 – объемная плотность заряда внутри замкнутой поверхности;
– объемная плотность заряда внутри замкнутой поверхности; 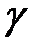 – удельная проводимость вещества.
– удельная проводимость вещества.
Для стационарных полей (E=const, B=const) уравнения Максвелла принимают вид
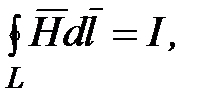
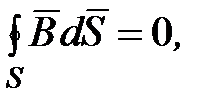
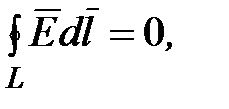
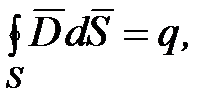
то есть источниками магнитного поля в данном случае являются только
токи проводимости, а источниками электрического поля – только электрические заряды. В этом частном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрические и магнитные поля.
Используя известные из векторного анализа теоремы Стокса и Гаусса, можно представить полную систему уравнений Максвелла в дифференциальной форме (характеризующих поле в каждой точке пространства):
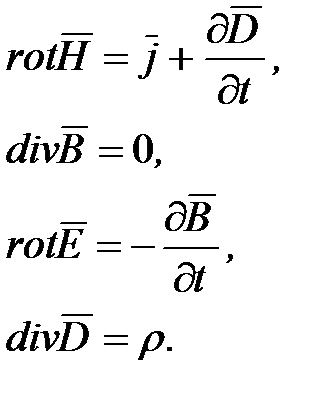 (5.7)
(5.7)
Очевидно, что уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе
существуют электрические заряды, но нет зарядов магнитных.
Уравнения Максвелла – наиболее общие уравнения для электрических
и магнитных полей в покоящихся средах. Они играют в учении об электромагнетизме ту же роль, что и законы Ньютона в механике.
Электромагнитной волной называют переменное электромагнитное поле, распространяющееся в пространстве с конечной скоростью.
Существование электромагнитных волн вытекает из уравнений Максвелла, сформулированных в 1865 г. на основе обобщения эмпирических законов электрических и магнитных явлений. Электромагнитная волна образуется вследствие взаимной связи переменных электрического и магнитного полей – изменение одного поля приводит к изменению другого, то есть чем быстрее меняется во времени индукция 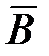 магнитного поля, тем больше напряженность
магнитного поля, тем больше напряженность 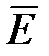 электрического поля, и наоборот. Таким образом, для образования интенсивных электромагнитных волн необходимо возбудить электромагнитные колебания достаточно высокой частоты. Фазовая скорость электромагнитных волн определяется
электрического поля, и наоборот. Таким образом, для образования интенсивных электромагнитных волн необходимо возбудить электромагнитные колебания достаточно высокой частоты. Фазовая скорость электромагнитных волн определяется
электрическими и магнитными свойствами среды:
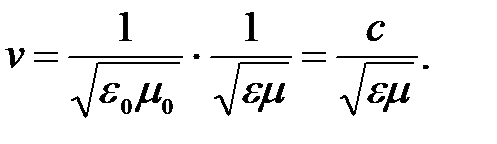
В вакууме ( 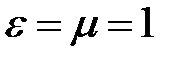 ) скорость распространения электромагнитных волн совпадает со скоростью света; в веществе
) скорость распространения электромагнитных волн совпадает со скоростью света; в веществе 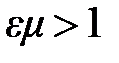 , поэтому скорость распространения электромагнитных волн в веществе всегда меньше, чем в вакууме.
, поэтому скорость распространения электромагнитных волн в веществе всегда меньше, чем в вакууме.
Электромагнитные волны являются поперечными волнами –
колебания векторов 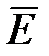 и
и 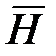 происходят во взаимно перпендикулярных плоскостях, причем векторы
происходят во взаимно перпендикулярных плоскостях, причем векторы 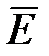 ,
, 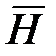 и
и 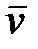 образуют правовинтовую систему. Из уравнений Максвелла также следует, что в электромагнитной волне векторы
образуют правовинтовую систему. Из уравнений Максвелла также следует, что в электромагнитной волне векторы 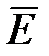 и
и 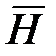 всегда колеблются в одинаковых фазах, а мгновенные значения Е и Н в любой точке связаны соотношением
всегда колеблются в одинаковых фазах, а мгновенные значения Е и Н в любой точке связаны соотношением
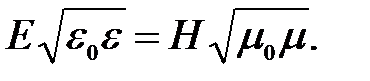
Уравнения плоской электромагнитной волны в векторной форме:
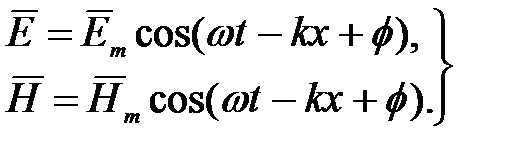 (6.66)
(6.66)
|
|
| y |
| z |
| x |
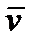
|
| Рис. 6.21 |
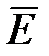 и
и 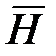 образуют с направлением распространения волны правовинтовую систему. В фиксированной точке пространства векторы напряженности электрического и магнитного полей изменяются со временем по гармоническому закону.
образуют с направлением распространения волны правовинтовую систему. В фиксированной точке пространства векторы напряженности электрического и магнитного полей изменяются со временем по гармоническому закону.
Для характеристики переноса энергии любой волной в физике введена векторная величина, называемая плотностью потока энергии 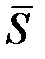 . Она численно равна количеству энергии, переносимой в единицу времени через единичную площадку, перпендикулярную к направлению, в котором
. Она численно равна количеству энергии, переносимой в единицу времени через единичную площадку, перпендикулярную к направлению, в котором
распространяется волна. Направление вектора 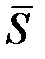 совпадает с направлением переноса энергии. Величину плотности потока энергии можно получить, умножив плотность энергии
совпадает с направлением переноса энергии. Величину плотности потока энергии можно получить, умножив плотность энергии 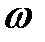 на скорость волны
на скорость волны
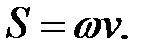
Плотность энергии 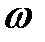 электромагнитного поля слагается из плотности энергии электрического поля и плотности энергии магнитного поля:
электромагнитного поля слагается из плотности энергии электрического поля и плотности энергии магнитного поля:
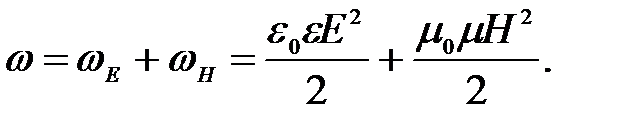
или
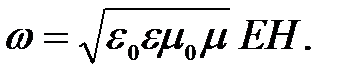 (6.67)
(6.67)
Умножив плотность энергии электромагнитной волны на ее фазовую скорость, получим плотность потока энергии
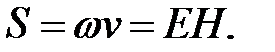 (6.68)
(6.68)
Векторы 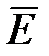 и
и 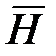 взаимно перпендикулярны и образуют с направлением распространения волны правовинтовую систему. Поэтому направление
взаимно перпендикулярны и образуют с направлением распространения волны правовинтовую систему. Поэтому направление
вектора 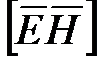 совпадает с направлением переноса энергии, а модуль этого вектора определяется соотношением (6.68). Следовательно, вектор плотности потока энергии электромагнитной волны можно представить как векторное произведение
совпадает с направлением переноса энергии, а модуль этого вектора определяется соотношением (6.68). Следовательно, вектор плотности потока энергии электромагнитной волны можно представить как векторное произведение
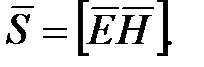 (6.69)
(6.69)
Вектор 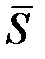 называют вектором Умова-Пойнтинга.
называют вектором Умова-Пойнтинга.
Колебания и волны
Тема 18. Свободные гармонические колебания
Движения, обладающие той или иной степенью повторяемости, называются колебаниями.
Если значения физических величин, изменяющихся в процессе движения, повторяются через равные промежутки времени, то такое движение называется периодическим (движение планет вокруг Солнца, движение поршня в цилиндре двигателя внутреннего сгорания и др.). Колебательную систему вне зависимости от ее физической природы называютосциллятором. Примером осциллятора может служить колеблющийся груз, подвешенный на пружине или нити.
Полным колебанием называют один законченный цикл колебательного движения, после которого оно повторяется в том же порядке.
По способу возбуждения колебания делят на:
· свободные (собственные), происходящие в представленной самой себе системе около положения равновесия после какого-либо первоначального воздействия;
· вынужденные, происходящие при периодическом внешнем воздействии;
· параметрические, происходящие при изменении какого-либо параметра колебательной системы;
· автоколебания, происходящие в системах, самостоятельно регулирующих поступление внешних воздействий.
Любое колебательное движение характеризуетсяамплитудой А — максимальным отклонением колеблющейся точки от положения равновесия.
Колебания точки, происходящие с постоянной амплитудой, называютнезатухающими,а колебания с постепенно уменьшающейся амплитудой – затухающими.
Время, в течение которого совершается полное колебание, называютпериодом (Т).
Частотой 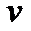 периодических колебаний называют число полных колебаний, совершаемых за единицу времени. Единица частоты колебаний — герц (Гц). Герц – это частота колебаний, период которых равен 1 с: 1 Гц = 1 с –1.
периодических колебаний называют число полных колебаний, совершаемых за единицу времени. Единица частоты колебаний — герц (Гц). Герц – это частота колебаний, период которых равен 1 с: 1 Гц = 1 с –1.
Циклической иликруговой частотой периодических колебаний называется число полных колебаний, совершаемых за время 2p с: 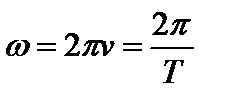 . [
. [ 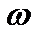 ]=рад/с.
]=рад/с.
Если положение тела в любой момент времени может быть описано единственным параметром, то тело имеет одну степень свободы. Такое колеблющееся тело называют одномерным осциллятором.
 Несмотря на большое разнообразие колебательных процессов, все они совершаются по некоторым общим закономерностям и могут быть сведены к совокупности простейших периодических колебаний, называемых гармоническими. Гармонические – это колебания, которые описываются периодическим законом:
Несмотря на большое разнообразие колебательных процессов, все они совершаются по некоторым общим закономерностям и могут быть сведены к совокупности простейших периодических колебаний, называемых гармоническими. Гармонические – это колебания, которые описываются периодическим законом: 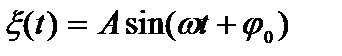 (1)
(1)
где 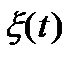 – периодически изменяющаяся величина (смещение, скорость, сила и т.д.), А – амплитуда.
– периодически изменяющаяся величина (смещение, скорость, сила и т.д.), А – амплитуда.
Система, закон движения которой имеет вид (1), называется одномерным (линейным) классическим гармоническим осциллятором или сокращенно гармоническим осциллятором.
Аргумент синуса или косинуса 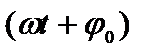 называется фазой колебаний. Фаза колебания определяет смещение в момент времени t. Начальная фаза
называется фазой колебаний. Фаза колебания определяет смещение в момент времени t. Начальная фаза 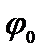 определяет смещение тела в момент начала отсчета времени.
определяет смещение тела в момент начала отсчета времени.
Фаза колебаний представляет собой угловую меру времени, прошедшего от начала колебаний.
 Рассмотрим смещение x колеблющегося тела относительно положения равновесия (
Рассмотрим смещение x колеблющегося тела относительно положения равновесия ( 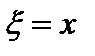 , рис.21.2, а). Уравнение гармонического колебания:
, рис.21.2, а). Уравнение гармонического колебания: 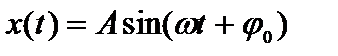
Первая производная от 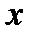 по времени дает выражение для скорости движения тела:
по времени дает выражение для скорости движения тела: 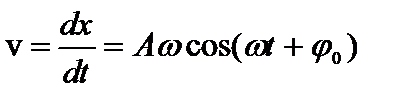 ; (2)
; (2)
Скорость достигает своего максимального значения в момент времени, когда 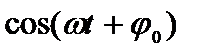 =1:
=1: 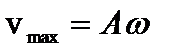 . Смещение же точки в этот момент рано нулю
. Смещение же точки в этот момент рано нулю 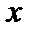 =0 (рис. 21.2, б).
=0 (рис. 21.2, б).
Ускорение изменяется со временем также по гармоническому закону:
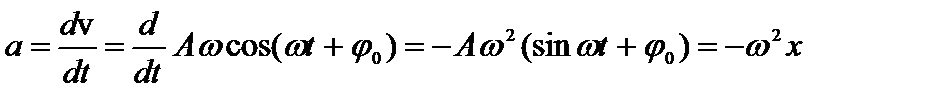 , (3)
, (3)
где 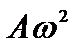 – максимальное значение ускорения. Знак минус означает, что ускорение направлено в сторону, противоположную смещению, т.е. ускорение и смещение изменяются в противофазе (рис. 21.2, в). Из рис. 21.2. видно, что скорость достигает максимального значения, когда колеблющаяся точка проходит положение равновесия. В этот момент смещение и ускорение равны нулю.
– максимальное значение ускорения. Знак минус означает, что ускорение направлено в сторону, противоположную смещению, т.е. ускорение и смещение изменяются в противофазе (рис. 21.2, в). Из рис. 21.2. видно, что скорость достигает максимального значения, когда колеблющаяся точка проходит положение равновесия. В этот момент смещение и ускорение равны нулю.
 Свободными (собственными) называются колебания, которые происходят в отсутствие переменных внешних воздействий на колебательную систему. Они возникают вследствие какого-либо начального отклонения этой системы от состояния ее устойчивого равновесия. Для того, чтобы тело совершало гармоническое колебательное движение, на него должна действовать сила, всегда направленная к положению равновесия, а по величине – прямо пропорциональная смещению от этого положения. Силы, направленные к положению равновесия, называются возвращающими.
Свободными (собственными) называются колебания, которые происходят в отсутствие переменных внешних воздействий на колебательную систему. Они возникают вследствие какого-либо начального отклонения этой системы от состояния ее устойчивого равновесия. Для того, чтобы тело совершало гармоническое колебательное движение, на него должна действовать сила, всегда направленная к положению равновесия, а по величине – прямо пропорциональная смещению от этого положения. Силы, направленные к положению равновесия, называются возвращающими.
Рассмотрим свободные колебания, происходящие в системе с одной степенью свободы. Пусть тело массой т укреплено на пружине, упругость которой k (пружинный маятник, рис.22.1). В отсутствие сил трения на тело, выведенное из положения равновесия, действует упругая сила пружины F= –kx. Тогда по второму закону динамики 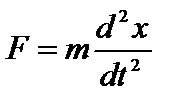 имеем:
имеем: 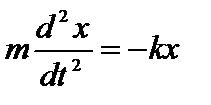 или
или 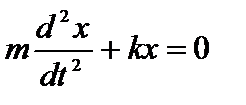 . (1)
. (1)
Если ввести обозначение 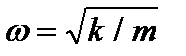 , то уравнение (1) можно переписать в следующем виде:
, то уравнение (1) можно переписать в следующем виде: 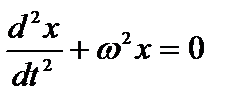 (2)
(2)
Это и есть дифференциальное уравнение свободных колебаний с одной степенью свободы. Его решением является функция вида 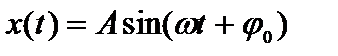 . Величина
. Величина 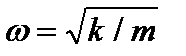 является циклической частотой колебаний. Период колебаний пружинного маятника:
является циклической частотой колебаний. Период колебаний пружинного маятника: 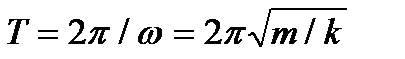 (3).
(3).
 Физический маятник. Его образует твердое тело, подвешенное в поле тяжести на закрепленной горизонтальной оси. Возвращающим моментом является момент силы тяжести
Физический маятник. Его образует твердое тело, подвешенное в поле тяжести на закрепленной горизонтальной оси. Возвращающим моментом является момент силы тяжести 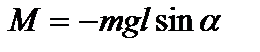 , где
, где 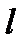 – расстояние от оси до центра тяжести тела. При малых значениях
– расстояние от оси до центра тяжести тела. При малых значениях 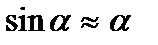 , тогда возвращающий момент:
, тогда возвращающий момент:  .
.
В соответствии с основным законом динамики вращения: 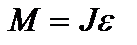 , где J – момент инерции маятника относительно оси, e – угловое ускорение.
, где J – момент инерции маятника относительно оси, e – угловое ускорение.
Так как 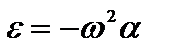 , то
, то 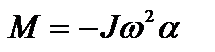 . Приравнивая два момента для одного тела, находим:
. Приравнивая два момента для одного тела, находим:

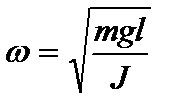 ;
; 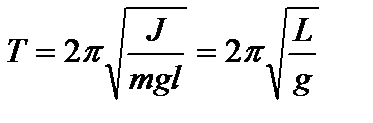 , (4)
, (4)
где 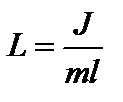 – приведенная длина физического маятника.
– приведенная длина физического маятника.
Математический маятник. Это модель, в которой вся масса сосредоточена в материальной точке, колеблющейся на невесомой и недеформируемой нити (рис.22.3).
При отклонении материальной точки от положения равновесия на малый угол a, такой, чтобы выполнялось условие 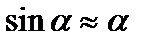 , на тело будет действовать возвращающая сила
, на тело будет действовать возвращающая сила 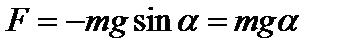 . Знак минус указывает, что сила направлена в сторону, противоположную смещению. Так как
. Знак минус указывает, что сила направлена в сторону, противоположную смещению. Так как 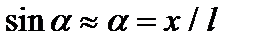 , то сила равна
, то сила равна 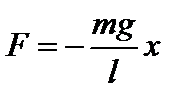 . Сила пропорциональна смещению, следовательно, под действием этой силы материальная точка будет совершать гармонические колебания. Обозначим
. Сила пропорциональна смещению, следовательно, под действием этой силы материальная точка будет совершать гармонические колебания. Обозначим 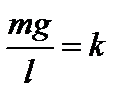 , где
, где 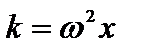 , имеем:
, имеем: 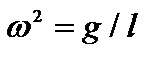 или
или 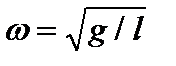 . Отсюда период колебаний математического маятника:
. Отсюда период колебаний математического маятника: 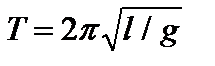 .
.
Дата добавления: 2016-10-26; просмотров: 2904;











