Энергия магнитного поля

Магнитное поле, подобно электрическому полю, является носителем энергии. Естественно предположить, что энергия магнитного поля равна той работе, которая затрачивается электрическим током на создание этого поля.

Рассмотрим контур индуктивностью L, по которому течет ток силой I.
С данным контуром сцеплен магнитный поток Ф=LI, причем при изменении тока на величину dI магнитный поток изменяется на dФ=LdI. Однако для изменения магнитного потока на величину dФ ток должен совершить работу

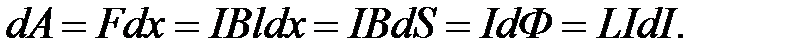
Тогда работа по созданию магнитного потока Ф, численно равная энергии магнитного поля, связанного с контуром, равна

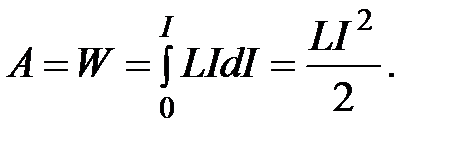(4.10)

Формулу (4.10) можно получить также, воспользовавшись законом Ома. При изменении тока I в замкнутом контуре возникает ЭДС самоиндукции, противодействующая этому изменению. По закону Ома сила тока в контуре с сопротивлением R и индуктивностью L равна

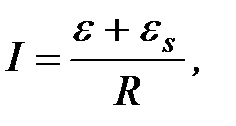
где 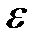– ЭДС источника электроэнергии; 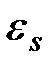– ЭДС самоиндукции, которая по закону Фарадея равна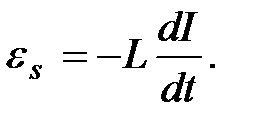

Таким образом,

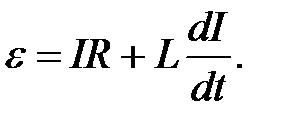
Работа, совершаемая источником электроэнергии за время dt, равна

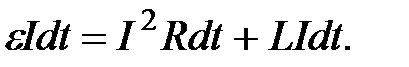
Первое слагаемое в правой части выражения представляет собой
джоулеву работу, расходуемую на нагревание проводника, второе – дополнительную работу, обусловленную индукционными явлениями. Следовательно, работа, затрачиваемая на увеличение силы тока в контуре от нуля до I, равна

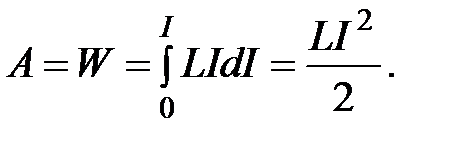
Таким образом, увеличение силы тока в проводнике вызывает соответствующее усиление его магнитного поля и увеличение энергии магнитного поля этого контура с током.

Формула (4.10) позволяет также дать следующее энергетическое определение индуктивности: индуктивность контура численно равна удвоенной энергии магнитного поля, создаваемого проходящим по контуру током единичной силы.