Закон Ома в интегральной форме

Для однородного участка цепи, то есть для участка, на котором не действуют сторонние силы, закон Ома записывается в форме (2.8). Рассмотрим теперь неоднородный участок цепи 1-2 (рис. 2.8), где действует ЭДС источника 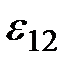и на концах которого приложена разность потенциалов .

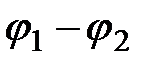P AAAA//8DAFBLAwQUAAYACAAAACEAl4xLNeAAAAALAQAADwAAAGRycy9kb3ducmV2LnhtbEyPwU7D MAyG70i8Q2QkLmhLKKwaXdMJTdoRNFYkrmnrpdUap2qyrfD0mBO72fKn39+fryfXizOOofOk4XGu QCDVvunIavgst7MliBANNab3hBq+McC6uL3JTdb4C33geR+t4BAKmdHQxjhkUoa6RWfC3A9IfDv4 0ZnI62hlM5oLh7teJkql0pmO+ENrBty0WB/3J6fBHn/s5q2Mbhuncrcj+fD1VL1rfX83va5ARJzi Pwx/+qwOBTtV/kRNEL2GRC25S9QwW6Q8MPGSpAsQFaPqWYEscnndofgFAAD//wMAUEsBAi0AFAAG AAgAAAAhALaDOJL+AAAA4QEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQ SwECLQAUAAYACAAAACEAOP0h/9YAAACUAQAACwAAAAAAAAAAAAAAAAAvAQAAX3JlbHMvLnJlbHNQ SwECLQAUAAYACAAAACEAyqttX88IAAAUcAAADgAAAAAAAAAAAAAAAAAuAgAAZHJzL2Uyb0RvYy54 bWxQSwECLQAUAAYACAAAACEAl4xLNeAAAAALAQAADwAAAAAAAAAAAAAAAAApCwAAZHJzL2Rvd25y ZXYueG1sUEsFBgAAAAAEAAQA8wAAADYMAAAAAA== ">

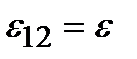
I

R

-

а

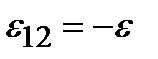
R

I

-

+

б

Рис. 2.8

+

На рассматриваемом участке работа 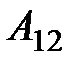всех приложенных сил (сторонних и электростатических), совершаемая над носителями тока, согласно (2.6) равна:

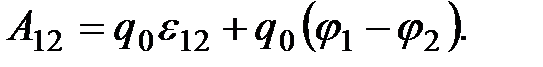
В этой формуле ЭДС 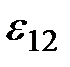берется либо с положительным, либо с отрицательным знаком. Если ЭДС способствует движению положительных
зарядов в направлении обхода (в направлении 1-2), то есть внутри источника обход совпадает с перемещением зарядов от катода к аноду, то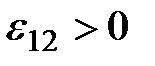
(рис. 2.8, а). Если ЭДС препятствует движению положительных зарядов
в направлении обхода, то 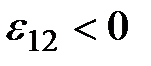(рис. 2.8, б).

По закону сохранения и превращения энергии работа 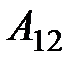равна теплоте, выделяющейся на участке 1-2 за время t (эта теплота определяется согласно закону Джоуля-Ленца):

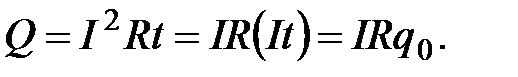(2.20)

Приравнивая (2.6) и (2.20), получим

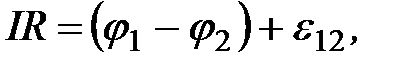(2.21)

или

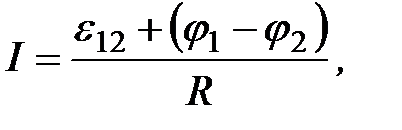(2.22)

где R – суммарное сопротивление, включающее в себя внутреннее сопротивление r источника тока и сопротивление внешней цепи.

Выражение (2.21) или (2.22) есть закон Ома в интегральной (обобщенной) форме для цепи постоянного тока.

Действительно, если на данном участке цепи источник тока отсутствует ( 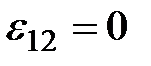), то из (2.22) приходим к закону Ома для однородного участка цепи:

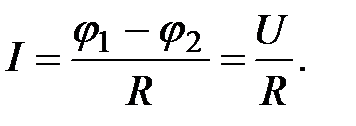
Если электрическая цепь замкнута (точки 1 и 2 совпадают), то 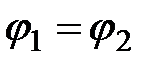. Тогда из (2.22) получаем закон Ома для замкнутой цепи:

.

R

r

R

I

вн.

+

=

=

e

e

Наконец, если цепь разомкнута, то 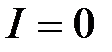и из (2.22) получаем, что 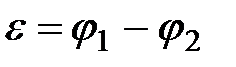, следовательно, для экспериментального определения ЭДС
источника тока необходимо измерить разность потенциалов на его зажимах при разомкнутой нагрузке (режим холостого хода цепи).