Электричество и магнетизм
Тема 11. Основные характеристики и закономерности электростатики
Взаимодействие между электрически заряженными частицами или телами осуществляется посредством электромагнитного поля, которое представляет собой совокупность двух взаимосвязанных силовых полей – электрического и магнитного. Раздел физической науки, в котором изучаются законы электромагнитного поля, называется электродинамикой.
Характерной особенностью электрического поля является то, что оно действует как на неподвижные, так и на движущиеся заряженные тела. Характерная особенность магнитного поля состоит в том, что оно действует только на движущиеся заряженные частицы (сила Лоренца, сила Ампера).
Электрическое поле неподвижных заряженных тел, осуществляющее взаимодействие между ними, называется электростатическим полем.
Для того чтобы количественно охарактеризовать способность тел вступать в электрическое взаимодействие, в электродинамике введено понятие электрического заряда. Электрический заряд – это физическая величина, характеризующая свойство тел или частиц вступать в электромагнитное взаимодействие.
В природе существуют два рода электрических зарядов – положительные и отрицательные. Разноименно заряженные тела притягиваются, а одноименно заряженные отталкиваются друг от друга.
Опытным путем установлено, что электрический заряд обладает свойством дискретности, то есть заряд 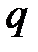 любого тела состоит из целого числа
любого тела состоит из целого числа 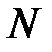 элементарных зарядов, приближенно равных
элементарных зарядов, приближенно равных 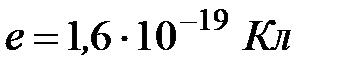 (
( 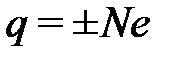 ). Носителями элементарного отрицательного и положительного зарядов являются соответственно электрон (масса покоя
). Носителями элементарного отрицательного и положительного зарядов являются соответственно электрон (масса покоя 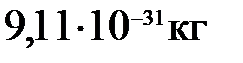 )
)
и протон (масса покоя 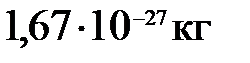 ). Электроны и протоны входят в состав всех атомов и молекул. Элементарный заряд впервые был измерен
). Электроны и протоны входят в состав всех атомов и молекул. Элементарный заряд впервые был измерен
Р.Э. Милликеном в 1909 г.
Система тел или частиц называется электрически изолированной, или замкнутой, если между нею и внешними телами отсутствует обмен электрическими зарядами. В результате обобщения опытных данных был установлен фундаментальный закон природы – закон сохранения электрического заряда: алгебраическая сумма электрических зарядов любой электрически замкнутой системы сохраняется, какие бы процессы ни происходили внутри этой системы, то есть
| ∑ |
| = |
| = |
| n |
| i |
| i |
| сonst, |
| q |
| (1.1) |
где n – количество зарядов в системе. Другими словами, в замкнутой системе могут образовываться или исчезать электрически заряженные частицы;
однако при этом одновременно рождаются или исчезают частицы,
заряды которых противоположны по знаку и в сумме равны нулю. Например, при ионизации нейтрального атома образуется пара частиц – свободный электрон и положительный ион, однако алгебраическая сумма зарядов остается неизменной.
Во многих задачах электродинамики пользуются моделью точечного электрического заряда. Точечный электрический заряд – это заряженное тело, размерами и формой которого можно пренебречь в рассматриваемой задаче. Например, изучая электростатическое взаимодействие двух заряженных тел, их можно считать точечными зарядами, если размеры этих тел
намного меньше расстояния между ними.
Единица электрического заряда в СИ – кулон (Кл): 1 Кл – это электрический заряд, проходящий за 1 с через поперечное сечение проводника при силе тока 1 А.
Закон взаимодействия неподвижных точечных электрических зарядов экспериментально установлен в 1785 г. французским физиком Ш. Кулоном с помощью крутильных весов. Поэтому силы электростатического взаимодействия часто называют кулоновскими силами. Этот закон формулируется следующим образом: сила взаимодействия между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна
произведению модулей этих зарядов, обратно пропорциональна квадрату расстояния между ними и направлена вдоль соединяющей их прямой.
Закон Кулона в векторной форме записывается в виде
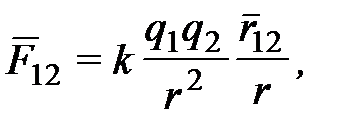
или
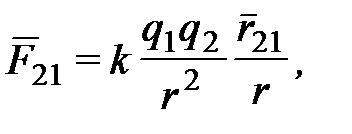 (1.2)
(1.2)
где 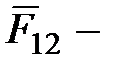 сила, действующая на заряд
сила, действующая на заряд 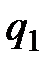 со стороны заряда
со стороны заряда 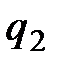 ;
; 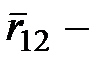
радиус-вектор, соединяющий заряд 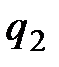 с зарядом
с зарядом 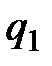 ;
; 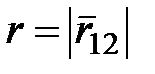 ;
;  коэффициент пропорциональности, зависящий от выбора системы единиц физических величин. На заряд
коэффициент пропорциональности, зависящий от выбора системы единиц физических величин. На заряд 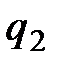 со стороны заряда
со стороны заряда 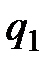 действует сила
действует сила 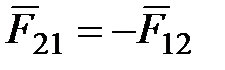 ,
,
то есть взаимодействие электрических точечных зарядов подчиняется третьему закону Ньютона (рис. 1.1).
В скалярной форме закон Кулона имеет следующий вид:
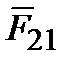
|
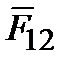
|
|
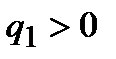
|
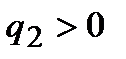
|
| Рис. 1.1 |
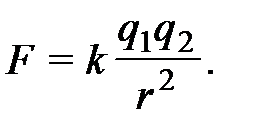
Коэффициент пропорциональности k в СИ равен
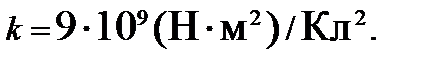
Если неподвижные точечные электрические заряды взаимодействуют
в какой-либо среде (масле, керосине и т. п.), то сила взаимодействия между ними определяется выражением
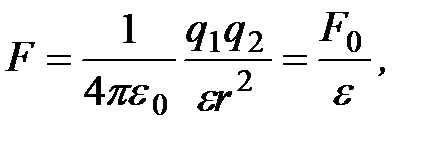 (1.4)
(1.4)
| + |
| . |
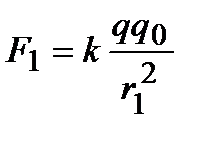
|
| . |
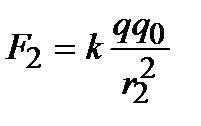
|
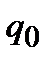
|
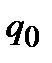
|
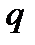
|
| Рис. 1.2 |
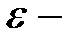 диэлектрическая проницаемость среды (
диэлектрическая проницаемость среды ( 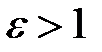 );
); 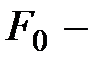 сила взаимодействия между теми же зарядами в вакууме. Следовательно,
сила взаимодействия между теми же зарядами в вакууме. Следовательно, 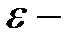 это безразмерная физическая величина, показывающая, во сколько раз кулоновское взаимодействие между двумя точечными электрическими зарядами в данной среде меньше, чем в вакууме.
это безразмерная физическая величина, показывающая, во сколько раз кулоновское взаимодействие между двумя точечными электрическими зарядами в данной среде меньше, чем в вакууме.
Если в пространство, окружающее электрический заряд, внести другой заряд, то между ними возникнет кулоновское взаимодействие. Следовательно, в пространстве, окружающем электрические заряды, существует силовое поле, в данном случае электрическое поле, являющееся средой взаимодействия между зарядами. Так как рассматриваются неподвижные заряды,
то поле, создаваемое ими, называется электростатическим.
Напряженность является силовой характеристикой электростатического поля.
Напряженность электростатического поля в данной точке есть векторная физическая величина, определяемая силой, действующей со стороны поля на неподвижный единичный пробный заряд, помещенный в эту точку поля:
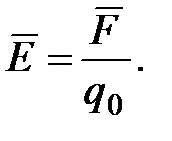 (1.5)
(1.5)
| + |
| – |
| . |
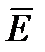
|
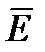
|
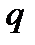
|
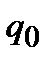
|
|
| Рис. 1.3 |
|
| . |
напряженность поля точечного электрического заряда в вакууме
| . |
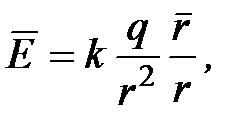
или в скалярной форме
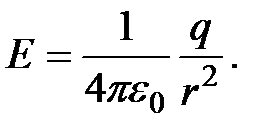 (1.6)
(1.6)
Направление вектора 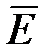 совпадает с направлением силы, действующей на положительный заряд.
совпадает с направлением силы, действующей на положительный заряд.
Из формулы (1.5) следует, что единица напряженности электростатического поля – ньютон на кулон (Н/Кл): 1 Н/Кл – напряженность
такого поля, которое на точечный заряд в 1 Клдействует с силой 1 Н.
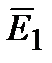
|
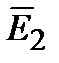
|
| 1 |
| 2 |
| Рис. 1.4 |
совпадают с направлением вектора
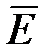 (рис. 1.4). Силовым линиям поля приписывается направление, совпадающее с направлением вектора напряженности. Так как в каждой данной точке пространства вектор
(рис. 1.4). Силовым линиям поля приписывается направление, совпадающее с направлением вектора напряженности. Так как в каждой данной точке пространства вектор 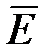 имеет лишь одно направление, то линии напряженности никогда не пересекаются. Густотой силовых линий характеризуют напряженность поля: в местах, где напряженность поля меньше, линии проходят реже. Примеры простейших электростатических полей приведены на рис. 1.5, а – в.
имеет лишь одно направление, то линии напряженности никогда не пересекаются. Густотой силовых линий характеризуют напряженность поля: в местах, где напряженность поля меньше, линии проходят реже. Примеры простейших электростатических полей приведены на рис. 1.5, а – в.
| + |
| – |
| + |
| – |
| а |
| б |
| в |
| Рис. 1.5 |
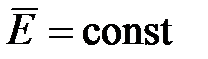 ).
). Примером такого поля может быть электростатическое поле плоского
конденсатора вдали от краев его обкладок.
принцип суперпозиции (наложения) электростатических полей: напряженность результирующего поля, создаваемого в данной точке пространства системой зарядов или заряженных тел, равна геометрической сумме напряженностей полей, создаваемых
в этой точке каждым из зарядов системы в отдельности. 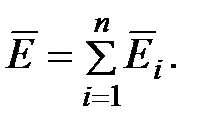
Потенциал является энергетической характеристикой электростатического поля:
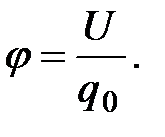 (1.16)
(1.16)
Таким образом, потенциал в какой-либо точке электростатического поля есть физическая скалярная величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку.
Из формулы (1.16) с учетом (1.14) следует, что потенциал точки поля
точечного заряда 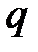
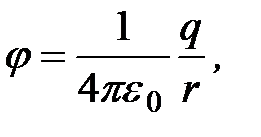 (1.17)
(1.17)
где r – расстояние от заряда до заданной точки.
Работа, совершаемая силами электростатического поля по перемещению заряда 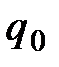 из точки 1 в точку 2 может быть представлена как
из точки 1 в точку 2 может быть представлена как  (1.18)
(1.18)
то есть работа кулоновских сил численно равна произведению величины
перемещаемого заряда на разность потенциалов в начальной и конечной точках поля. Из формулы (1.18) следует, что разность потенциалов двух точек электростатического поля – это физическая скалярная величина, определяемая работой, совершаемой кулоновскими силами при перемещении единичного положительного заряда из одной точки в другую.
Если перемещать заряд 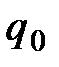 из произвольной точки за пределы поля,
из произвольной точки за пределы поля,
то есть в бесконечность, где по условию потенциал равен нулю, то согласно (1.18) работа сил электростатического поля 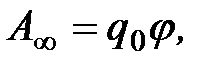 откуда
откуда
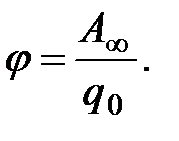 (1.19)
(1.19)
Таким образом, потенциал – это физическая величина, определяемая работой по перемещению единичного положительного заряда из данной точки поля в бесконечность.
Единица потенциала – вольт (В): 1 В – это потенциал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией в 1 Дж (см. формулу (1.16)): 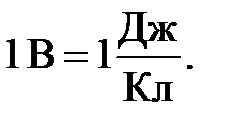
Из формул (1.15) и (1.16) вытекает, что если электростатическое поле создается несколькими зарядами, то потенциал точки поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов:
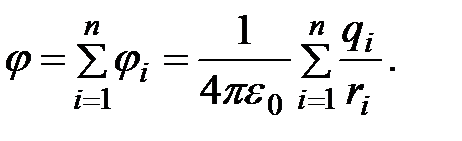
Напряженность и потенциал – различные характеристики одной и той же точки поля. Следовательно, между ними должна существовать однозначная связь.
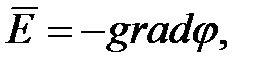 (1.21)
(1.21)
то есть напряженность поля равна градиенту потенциала со знаком «минус». Это означает, что вектор напряженности электростатического поля
направлен в сторону убывания потенциала.
В случае однородного поля (например, поля плоского конденсатора)
модуль напряженности определяется по формуле
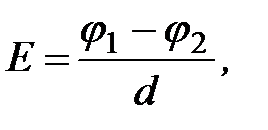 (1.22)
(1.22)
где d – расстояние, 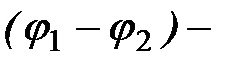 разность потенциалов между обкладками конденсатора. Из формулы (1.22) следует, что напряженность электрического поля можно выражать в вольтах на метр (В/м).
разность потенциалов между обкладками конденсатора. Из формулы (1.22) следует, что напряженность электрического поля можно выражать в вольтах на метр (В/м).
| + |
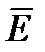
|
| Рис. 1.9 |
 имеет одно и то же значение. Если поле создается точечным зарядом (рис. 1.9), то его потенциал равен
имеет одно и то же значение. Если поле создается точечным зарядом (рис. 1.9), то его потенциал равен 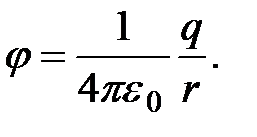 Таким образом,
Таким образом, эквипотенциальные поверхности в данном случае – концентрические сферы, охватывающие заряд. С другой стороны, линии напряженности поля точечного заряда – радиальные прямые. Следовательно, линии напряженности в случае точечного заряда перпендикулярны эквипотенциальным поверхностям.
Можно доказать, что силовые линии поля всегда нормальны к эквипотенциальным поверхностям. Эквипотенциальных поверхностей вокруг каждого заряда и системы
зарядов можно провести бесчисленное множество. Обычно их проводят так, чтобы разности потенциалов между любыми двумя соседними поверхностями были одинаковы. Тогда густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках: там, где эти поверхности расположены гуще, напряженность поля больше.
Вычисление напряженности поля большой системы электрических зарядов с помощью принципа суперпозиции электростатических полей можно
существенно упростить, используя теорему Гаусса. Эта теорема определяет поток вектора напряженности электрического поля через произвольную замкнутую поверхность.
Для произвольной замкнутой поверхности S поток вектора напряженности 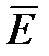 через эту поверхность определяется выражением
через эту поверхность определяется выражением
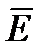
|
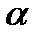
|
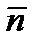
|
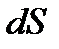
|
| Рис. 1.10 |
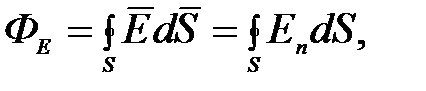 (1.23)
(1.23)
где  проекция вектора
проекция вектора 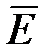 на нормаль
на нормаль 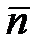
к площадке dS (рис. 1.10); 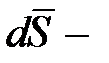 вектор, модуль которого равен dS, а направление совпадает с направлением нормали к площадке (
вектор, модуль которого равен dS, а направление совпадает с направлением нормали к площадке ( 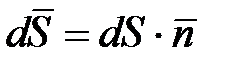 ).
).
Рассмотрим сферическую поверхность радиуса r, охватывающую точечный заряд q, находящийся в ее центре (рис. 1.11). В соответствии с формулой (1.23) поток вектора напряженности сквозь эту поверхность равен
| r |
| q |
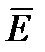
|
| Рис. 1.11 |
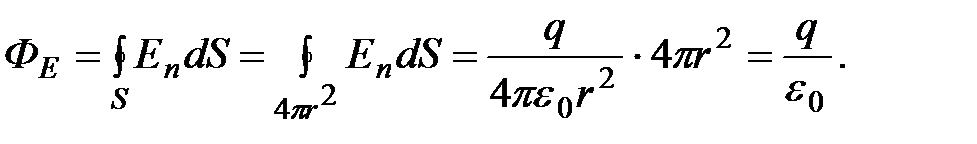 (1.24)
(1.24)
Этот результат справедлив для замкнутой
поверхности любой формы.
Рассмотрим теперь общий случай произвольной замкнутой поверхности, окружающей n зарядов. Тогда
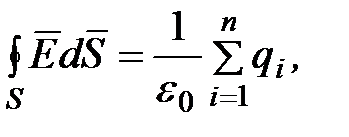 (1.25)
(1.25)
то есть поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на электрическую постоянную.
Применим теорему Гаусса для определения напряженности поля равномерно заряженной бесконечной плоскости. В этом случае ее поверхностная плотность заряда 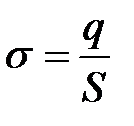 одинакова в любом месте плоскости. Это означает, что линии напряженности перпендикулярны плоскости в любой точке, то есть поле заряженной плоскости однородно (рис. 1.12).
одинакова в любом месте плоскости. Это означает, что линии напряженности перпендикулярны плоскости в любой точке, то есть поле заряженной плоскости однородно (рис. 1.12).
Мысленно выделим в пространстве цилиндр, ось которого перпендикулярна плоскости и одно из оснований проходит через интересующую нас точку. Согласно теореме Гаусса,
| S |

|
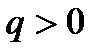
|
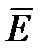
|
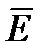
|
| Рис. 1.12 |
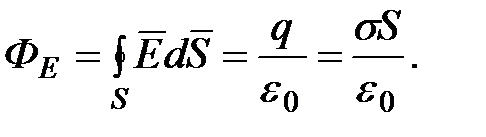
С другой стороны, так как линии
напряженности пересекают только
основания цилиндра, поток вектора 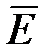 можно выразить через напряженность электрического поля у обоих оснований цилиндра, то есть
можно выразить через напряженность электрического поля у обоих оснований цилиндра, то есть
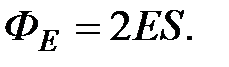
Тогда
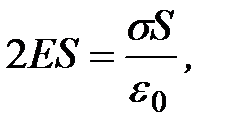 откуда
откуда
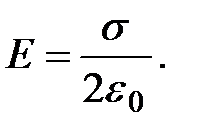 (1.26)
(1.26)
Приведем (без вывода) выражения для расчета напряженности электростатического поля, образованного некоторыми другими заряженными телами:
1. Напряженность поля, создаваемого разноименно заряженными параллельными бесконечно протяженными плоскостями (поле плоского конденсатора)
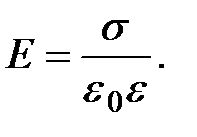 (1.27)
(1.27)
2. Напряженность поля, образованного заряженным шаром
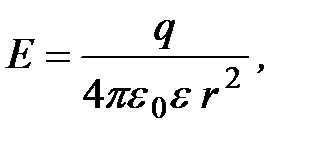 (1.28)
(1.28)
где 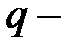 заряд шара радиуса
заряд шара радиуса 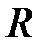 ;
; 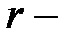 расстояние от центра шара до точки поля (
расстояние от центра шара до точки поля ( 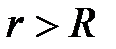 ).
).
3. Напряженность поля равномерно заряженной бесконечно длинной
нити (цилиндра)
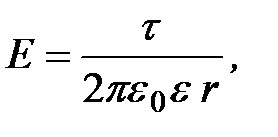 (1.29)
(1.29)
где 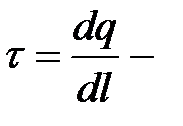 линейная плотность заряда на нити (заряд, приходящийся
линейная плотность заряда на нити (заряд, приходящийся
на единицу длины); 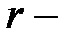 расстояние от нити до точки поля.
расстояние от нити до точки поля.
Тема 12. Проводники и диэлектрики в электрическом поле
Диэлектриками называют вещества, которые при обычных условиях практически не проводят электрический ток. Согласно представлениям классической физики, в диэлектриках, в отличие от проводников, нет свободных зарядов – заряженных частиц, которые могли бы прийти под действием электрического поля в упорядоченное движение и образовать электрический ток. К диэлектрикам относятся все газы, если они не подвергаются ионизации, некоторые жидкости (бензол, растительные и синтетические масла) и твердые вещества (фарфор, стекло, парафин, кварц и др.). Удельное электрическое сопротивление диэлектриков ρ~ 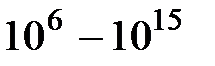 Ом·м,
Ом·м,
тогда как у металлических проводников ρ~ 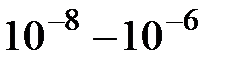 Ом·м.
Ом·м.
Все молекулы диэлектрика электрически нейтральны, то есть суммарный заряд электронов и атомных ядер, входящих в состав молекулы, равен нулю. Тем не менее, молекулы обладают электрическими свойствами.
| . |
| . |
| 1 |
| 2 |
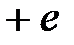
|
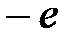
|
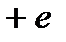
|
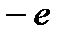
|

|
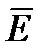
|
| а |
| б |
| Рис. 1.13 |
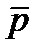
|
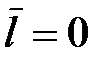 ) и дипольные моменты равны нулю.
) и дипольные моменты равны нулю.
Если поместить неполярный диэлектрик (бензол, парафин, полиэтилен, N2, H2, O2 и др.) во внешнее электрическое поле напряженностью 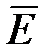 , то происходит деформация электронных оболочек атомов и молекул (рис. 1.13, б): положительные и отрицательные заряды молекул смещаются в противоположные стороны и центры распределения этих зарядов перестают совпадать (
, то происходит деформация электронных оболочек атомов и молекул (рис. 1.13, б): положительные и отрицательные заряды молекул смещаются в противоположные стороны и центры распределения этих зарядов перестают совпадать ( 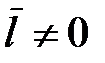 ). Такие деформированные молекулы можно рассматривать как электрические диполи, оси которых направлены вдоль поля.
). Такие деформированные молекулы можно рассматривать как электрические диполи, оси которых направлены вдоль поля.
Таким образом, неполярная молекула диэлектрика приобретает во внешнем электрическом поле индуцированный (наведенный) дипольный момент  , пропорциональный напряженности внешнего поля
, пропорциональный напряженности внешнего поля
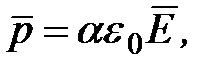
где 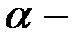 поляризуемость молекулы, зависящая только от ее объема. Неполярная молекула подобна упругому диполю, длина плеча которого пропорциональна растягивающей силе, то есть, пропорциональна напряженности
поляризуемость молекулы, зависящая только от ее объема. Неполярная молекула подобна упругому диполю, длина плеча которого пропорциональна растягивающей силе, то есть, пропорциональна напряженности 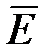 внешнего электрического поля.
внешнего электрического поля.
Диэлектрик называется полярным, если он состоит из молекул, у которых центры распределения положительных и отрицательных зарядов
не совпадают даже в отсутствие внешнего электрического поля ( 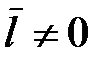 ). К полярным диэлектрикам относятся фенол, нитробензол и др.
). К полярным диэлектрикам относятся фенол, нитробензол и др.
Во внешнем электрическом поле напряженностью 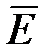 полярная молекула диэлектрика также деформируется, однако эта деформация незначительна
полярная молекула диэлектрика также деформируется, однако эта деформация незначительна
и можно считать, что полярная молекула по своим свойствам подобна
жесткому диполю, у которого имеется постоянный по модулю электрический момент ( 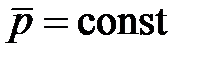 ).
).
Кроме рассмотренных двух групп различают кристаллическиедиэлектрики, имеющие ионную структуру, или слабополярныедиэлектрики. К ним относятся KCl, CsCl и др.
Смещение положительных и отрицательных зарядов диэлектрика во внешнем электрическом поле называется поляризацией. Другими словами, при внесении диэлектрика во внешнее электрическое поле в любом макроскопически малом объеме вещества 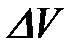 возникает отличный от нуля суммарный дипольный электрический момент молекул. Диэлектрик, находящийся в таком состоянии, называется поляризованным.
возникает отличный от нуля суммарный дипольный электрический момент молекул. Диэлектрик, находящийся в таком состоянии, называется поляризованным.
В зависимости от строения молекул диэлектрика различают три вида
поляризации.
1. Электронная (деформационная) поляризация. Она наблюдается
у неполярных диэлектриков. Под действием внешнего поля у молекул
диэлектриков этого типа возникают индуцированные дипольные моменты 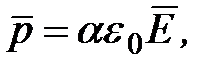 направленные вдоль поля, то есть по направлению вектора
направленные вдоль поля, то есть по направлению вектора  (рис. 1.13, б). Время установления этой поляризации порядка 10-15 с.
(рис. 1.13, б). Время установления этой поляризации порядка 10-15 с.
2. Дипольная (ориентационная) поляризация. Она наблюдается у полярных диэлектриков. Внешнее электрическое поле стремится ориентировать дипольные моменты полярных молекул – жестких диполей – по направлению вектора напряженности поля. Этому препятствует хаотическое тепловое движение молекул, вызывающее беспорядочный разброс диполей.
В итоге совместного действия поля и теплового движения возникает
преимущественная ориентация дипольных электрических моментов вдоль поля, возрастающая с увеличением напряженности 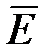 и с уменьшением температуры. Эта поляризация устанавливается за время порядка 10-10 с.
и с уменьшением температуры. Эта поляризация устанавливается за время порядка 10-10 с.
3. Ионная поляризация. Она происходит в твердых диэлектриках, имеющих ионную кристаллическую решетку. Внешнее электрическое поле вызывает
в таких диэлектриках смещение всех положительных ионов в направлении вектора напряженности 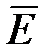 поля, а всех отрицательных ионов – в противоположную сторону. Это происходит за время порядка 10-13 с.
поля, а всех отрицательных ионов – в противоположную сторону. Это происходит за время порядка 10-13 с.
Количественной мерой поляризации диэлектрика служит вектор 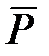 ,
,
называемый поляризованностью или вектором поляризации, равный отношению дипольного момента малого объема диэлектрика к этому объему:
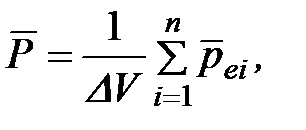 (1.30)
(1.30)
где 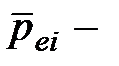 электрический дипольный момент i-молекулы; n – общее количество молекул в объеме
электрический дипольный момент i-молекулы; n – общее количество молекул в объеме 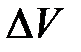 . Этот объем должен быть столь малым, чтобы
. Этот объем должен быть столь малым, чтобы
в его пределах электрическое поле можно было считать однородным.
В пределах малого объема 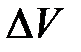 все молекулы неполярного диэлектрика приобретают в электрическом поле одинаковые индуцированные электрические моменты
все молекулы неполярного диэлектрика приобретают в электрическом поле одинаковые индуцированные электрические моменты 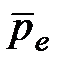 . Поэтому поляризованность неполярного диэлектрика в электрическом поле напряженностью
. Поэтому поляризованность неполярного диэлектрика в электрическом поле напряженностью 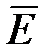 равна
равна
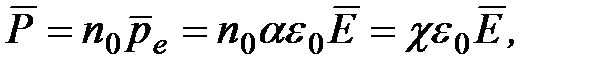 (1.31)
(1.31)
где n0 – концентрация молекул ( 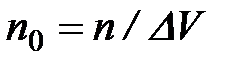 );
); 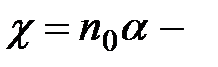 безразмерная величина, называемая диэлектрической восприимчивостью неполярного диэлектрика (
безразмерная величина, называемая диэлектрической восприимчивостью неполярного диэлектрика ( 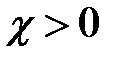 ).
).
Поляризованность полярного диэлектрика
| , |
| p |
| n |
| p |
| V |
| P |
| сp. |
| e |
| n |
| i |
| ei |
| = |
| å |
| = |
| = |
| D |
где 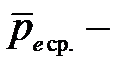 среднее значение вектора дипольного момента для всех n молекул, содержащихся в малом объеме
среднее значение вектора дипольного момента для всех n молекул, содержащихся в малом объеме 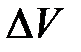 диэлектрика. Векторы
диэлектрика. Векторы 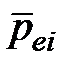 молекул –
молекул –
жестких диполей – одинаковы по модулю и отличаются только ориентациями в поле. В очень сильном электрическом поле и при достаточно
малой температуре электрические моменты 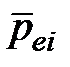 всех молекул располагаются практически параллельно вектору
всех молекул располагаются практически параллельно вектору 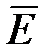 . При этом поляризованность полярного диэлектрика достигает максимального значения:
. При этом поляризованность полярного диэлектрика достигает максимального значения:
| . |
| p |
| n |
| P |
| e |
| max |
| = |
В результате поляризации на гранях диэлектрика появляются заряды, не компенсированные соседними диполями. Это приводит к тому, что на одной его поверхности возникают положительные заряды, а на другой – отрицательные. Эти электрические заряды называют связанными.
Внесем в однородное внешнее электростатическое поле 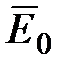 , создаваемое двумя бесконечными параллельными разноименно заряженными плоскостями, пластинку из однородного диэлектрика (рис. 1.15). Под влиянием поля диэлектрик
, создаваемое двумя бесконечными параллельными разноименно заряженными плоскостями, пластинку из однородного диэлектрика (рис. 1.15). Под влиянием поля диэлектрик
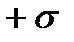
|

|
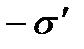
|
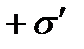
|
| – |
| – |
| – |
| + |
| + |
| + |
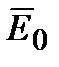
|
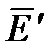
|
| Рис. 1.15 |
положительные смещаются вдоль поля,
отрицательные – против поля. В результате на правой грани диэлектрика будет избыток положительного заряда с поверхностной плотностью
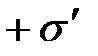 , на левой грани – избыток отрицательного заряда с поверхностной плотностью
, на левой грани – избыток отрицательного заряда с поверхностной плотностью 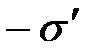 . Так как поверхностная плотность связанных зарядов
. Так как поверхностная плотность связанных зарядов  меньше плотности
меньше плотности 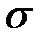 свободных зарядов плоскостей, то не всё поле
свободных зарядов плоскостей, то не всё поле  компенсируется полем зарядов диэлектрика: часть линий напряженности пройдет сквозь диэлектрик, другая же часть обрывается на связанных зарядах. Таким образом, поляризация диэлектрика вызывает ослабление в нем поля по сравнению с первоначальным внешним полем. Вне диэлектрика поле
компенсируется полем зарядов диэлектрика: часть линий напряженности пройдет сквозь диэлектрик, другая же часть обрывается на связанных зарядах. Таким образом, поляризация диэлектрика вызывает ослабление в нем поля по сравнению с первоначальным внешним полем. Вне диэлектрика поле 
Следовательно, появление связанных зарядов приводит к возникновению дополнительного поля напряженностью 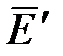 (поля, создаваемого связанными зарядами), которое направлено против внешнего поля
(поля, создаваемого связанными зарядами), которое направлено против внешнего поля 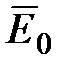 (поля, создаваемого свободными зарядами) и ослабляет его. Модуль напряжен-ности результирующего поля внутри диэлектрика
(поля, создаваемого свободными зарядами) и ослабляет его. Модуль напряжен-ности результирующего поля внутри диэлектрика
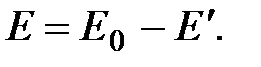
Напряженность поля, создаваемого двумя протяженными заряженными плоскостями, определяется по формуле (1.27), поэтому
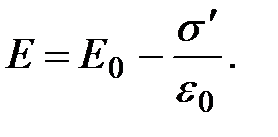 (1.32)
(1.32)
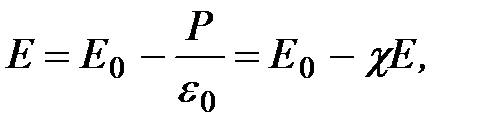
откуда напряженность результирующего поля внутри диэлектрика равна
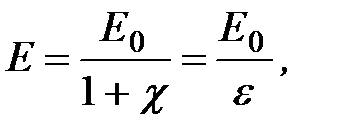 (1.34)
(1.34)
где безразмерная величина
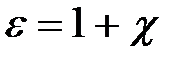 (1.35)
(1.35)
называется диэлектрической проницаемостью среды. Из (1.34) следует, что 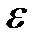 показывает, во сколько раз электрическое поле ослабляется диэлектриком, количественно характеризуя свойство диэлектрика поляризоваться во внешнем поле.
показывает, во сколько раз электрическое поле ослабляется диэлектриком, количественно характеризуя свойство диэлектрика поляризоваться во внешнем поле.
Как следует из формулы (1.34) напряженность электростатического поля зависит от свойств среды: в однородной изотропной среде напряженность поля обратно пропорциональна 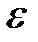 . Вектор напряженности
. Вектор напряженности 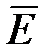 , переходя
, переходя
через границу диэлектриков, изменяется скачком, создавая затруднения при расчете электростатических полей. Поэтому помимо вектора напряженности поле характеризуется еще вектором электрического смещения (электрической индукции)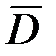 , который связан с вектором напряженности в электрически изотропной среде соотношением
, который связан с вектором напряженности в электрически изотропной среде соотношением
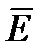
|

|
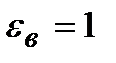
|
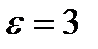
|
| а |
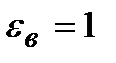
|
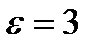
|
| б |
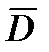
|
|
| Рис. 1.16 |
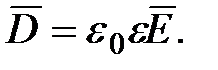 (1.36)
(1.36)
Так как в (1.36) 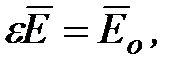 то
то 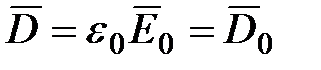 , то есть электрическое смещение внутри диэлектрика совпадает с электрическим смещением внешнего поля
, то есть электрическое смещение внутри диэлектрика совпадает с электрическим смещением внешнего поля 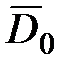 .
.
Теорема Гаусса для электростатического поля в диэлектрике формулируется следующим образом: поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов, то есть
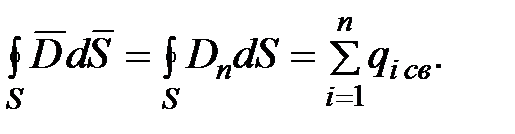 (1.37)
(1.37)
Дата добавления: 2016-10-26; просмотров: 2255;











