Работа и мощность тока. Закон Джоуля-Ленца

Рассмотрим однородный проводник, по концам которого приложено
напряжение 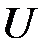. За время dt через поперечное сечение проводника переносится заряд 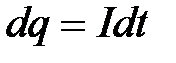. Так как ток представляет собой перемещение заряда dq под действием электрического поля, работа тока есть

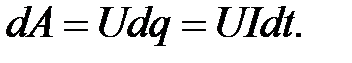(2.14)

Используя закон Ома для однородного участка цепи, формулу (2.14) можно представить в виде 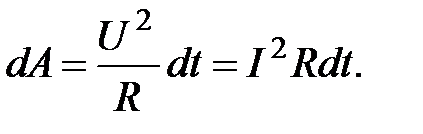(2.15)

Мощность электрического тока – это быстрота совершения работы,
то есть 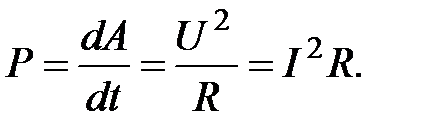(2.16)

Единица мощности – ватт: 1Вт – мощность, выделяемая в проводнике за 1с при протекании тока силой 1 А.

Если ток протекает по неподвижному металлическому проводнику,
то вся работа тока затрачивается на его нагревание и по закону сохранения энергии

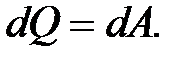
Таким образом, с учетом (2.14) и (2.15) получим

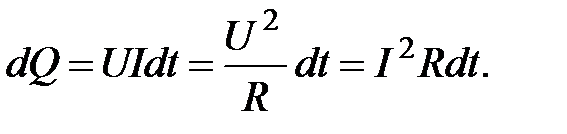(2.17)

Количество теплоты, выделяющееся за конечный промежуток времени от 0 до t при прохождении постоянного тока силой I найдем, интегрируя выражение (2.17): 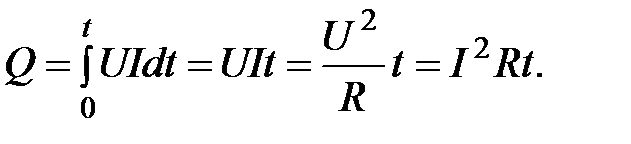(2.18)

Таким образом, количество теплоты, которое выделяется в проводнике с током, пропорционально квадрату силы тока, времени его протекания
и сопротивлению проводника. Выражение (2.18) есть закон Джоуля-Ленца для участка цепи постоянного тока. Он был установлен экспериментально Д. Джоулем (1841) и независимо от него Э.Х. Ленцем (1842).

Выделим в проводнике элементарный цилиндрический объем 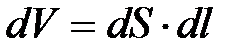(ось цилиндра совпадает с направлением тока). Сопротивление этого элементарного объема 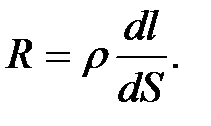Тогда по закону Джоуля-Ленца за время dt в этом объеме выделится теплота

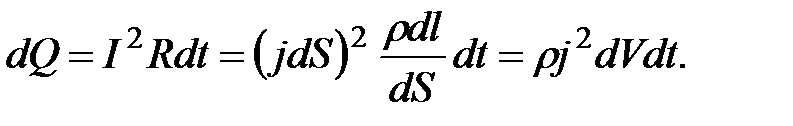
Количество теплоты, выделяющееся за единицу времени в единице объема, называется удельной тепловой мощностью электрического тока:

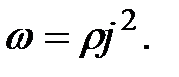
Используя дифференциальную форму закона Ома (2.11) и соотношение 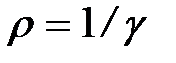, получим

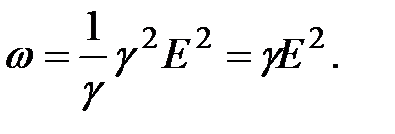(2.19)

Формула (2.19) является обобщенным выражением закона Джоуля-Ленца в дифференциальной форме, пригодным для любого проводника.