Термодинамика и молекулярная физика.
Тема 8. Феноменологическая термодинамика
Термодинамика изучает количественные закономерности превращения энергии, обусловленные тепловым движением молекул. Основу термодинамики составляют два фундаментальных закона, являющиеся обобщением многовекового опыта человеческой деятельности и называемых началами термодинамики. Первое начало описывает количественную и качественную стороны процессов превращения энергии; второе начало позволяет судить о направлении этих процессов.
Термодинамическая система – макроскопическое тело (или группа тел), которому свойственны процессы, сопровождающиеся переходом теплоты в другие виды энергии. Примером термодинамической системы может служить газ, заключенный в цилиндре под поршнем.
Состояние термодинамической системы однозначно определяется тремя параметрами: давлением, температурой и объемом, которые называются параметрами состояния.
Равновесное состояние термодинамической системы (или состояние термодинамического равновесия) – это состояние, при котором параметры состояния остаются неизменными сколь угодно долго при неизменных внешних условиях. Равновесное состояние на графике состояний описывается точкой.
Однако случается, что состояние системы не может быть определено каким-то одним значением параметра, например: неравномерно нагретое тело не может быть определено одним значением температуры. Состояния системы, которые не могут быть охарактеризованы одним каким-либо определенным значением параметра, являются неравновесными. Неравновесное состояние – состояние, при котором термодинамические параметры в различных точках различны.
Стационарное состояние термодинамической системы – состояние, при котором параметры состояния системы остаются постоянными во времени и во всех частях системы.
Термодинамический процесс – изменение состояния системы. Графическое изображение равновесного процесса называется диаграммой состояний.
Равновесный процесс – процесс, состоящий из непрерывной последовательности равновесных состояний. Равновесным может быть только бесконечно медленный обратимый процесс. Процессы, не удовлетворяющие этим требованиям, – неравновесные. Графически можно изображать только равновесные процессы – процессы, состоящие из последовательности равновесных состояний.
Все реальные процессы неравновесны (они протекают с конечной скоростью), но в ряде случаев неравновесностью реальных процессов можно пренебречь (чем медленнее процесс протекает, тем он ближе к равновесному). В дальнейшем рассматриваемые процессы будем считать равновесными.
Внутренней энергией термодинамической системы называется совокупность всех видов энергии, которыми она обладает, за вычетом энергии поступательного движения ее как целой и потенциальной энергии системы во внешнем поле. Под внутренней энергией U в термодинамике будем понимать энергию теплового движения частиц, образующих систему, и потенциальную энергию их взаимного положения.
Для идеального газа потенциальная энергия взаимодействия молекул считается равной нулю. Поэтому внутренняя энергия одного моля идеального газа равна:
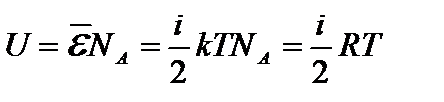 . (1)
. (1)
Из формулы (1) видим, что внутренняя энергия идеального газа пропорциональна абсолютная температуре.
Внутренняя энергия обладает следующими свойствами:
– в состоянии теплового равновесия частицы системы движутся так, что их полная энергия все время равна внутренней энергии;
– внутренняя энергия – величина аддитивная, т.е. внутренняя энергия системы тел равна сумме внутренних энергий образующих систему тел;
– внутренняя анергия системы является однозначной функцией ее состояния, т.е. каждому состоянию системы присуще только одно значение энергии; это означает, что изменение внутренней энергии при переходе из одного состояния в другое не зависит от пути перехода. Величина, изменение которой не зависит от пути перехода, в термодинамике называется функцией состояния:
DU=U2-U1 не зависит от вида процесса.
Или 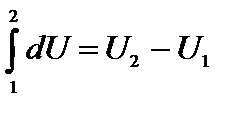 , где U2 и U1 – значения внутренней энергии в состояниях 1 и 2. Здесь dU – полный дифференциал.
, где U2 и U1 – значения внутренней энергии в состояниях 1 и 2. Здесь dU – полный дифференциал.
Изменение внутренней энергии системы может произойти, если:
– система получает извне или отдает окружающим телам некоторую энергию в какой-нибудь форме;
– система совершает работу против действующих на нее внешних сил.
Первое начало термодинамики выражает закон сохранения энергии для тех макроскопических явлений, в которых одним из существенных параметров, определяющих состояние тел, является температура.
Теплота, сообщенная системе в процессе изменения ее состояния, расходуется на изменение ее внутренней энергии и на совершение работы против внешних сил.
Q=DU + А (1)
Часто приходится разбивать рассматриваемый процесс на ряд элементарных процессов, каждый из которых соответствует весьма малому изменению параметров системы. Запишем уравнение (1) для элементарного процесса в дифференциальном виде: dQ=dU+dA, (2)
где dU — малое изменение внутренней энергии; dQ — элементарное количество теплоты; dА — элементарная работа.
Из уравнений (1) и (2) видно, что если процесс круговой, т.е. в результате него система возвращается в исходное состояние, то DU = 0 и, следовательно, Q=А. В круговом процессе все тепло, полученное системой, идет на производство внешней работы.
 Если U1=U2 и Q =А, то А = О. Это значит, что невозможен процесс, единственным результатом которого является, производство работы без каких бы то ни было изменений в других телах, т.е. невозможен перпетуум-мобиле (вечный двигатель) первого рода.
Если U1=U2 и Q =А, то А = О. Это значит, что невозможен процесс, единственным результатом которого является, производство работы без каких бы то ни было изменений в других телах, т.е. невозможен перпетуум-мобиле (вечный двигатель) первого рода.
 Рассмотрим процесс расширения газа. Пусть в цилиндрическом сосуде заключен газ, закрытый подвижным поршнем (рис.39.1). Предположим, что газ расширяется. Он будет перемещать поршень и совершать над ним работу. При малом смещении dx газ совершит работу dA=F•dx, где F –сила, с которой газ действует на поршень, р — давление газа в начале пути dx. Следовательно, dQ = pSdx = pdV, где dV — малое изменение объема газа. Работа, совершаемая при конечных изменениях объема, должна вычисляться путем интегрирования. Полная работа расширения:
Рассмотрим процесс расширения газа. Пусть в цилиндрическом сосуде заключен газ, закрытый подвижным поршнем (рис.39.1). Предположим, что газ расширяется. Он будет перемещать поршень и совершать над ним работу. При малом смещении dx газ совершит работу dA=F•dx, где F –сила, с которой газ действует на поршень, р — давление газа в начале пути dx. Следовательно, dQ = pSdx = pdV, где dV — малое изменение объема газа. Работа, совершаемая при конечных изменениях объема, должна вычисляться путем интегрирования. Полная работа расширения: 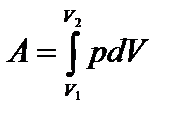 .
.
На графике (р,V) работа равна площади фигуры, ограниченной двумя ординатами и функцией p(V) (рис. 39.2).
Предположим, система переходит из одного состояния в другое, совершая работу по расширению, но двумя различными путями I и II: p1(V) и p2(V): 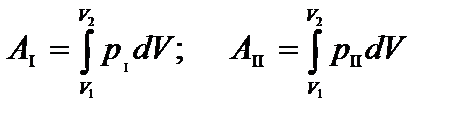
AI численно равна площади фигуры, ограниченной кривой I, АII – площади фигуры, ограниченной кривой II: AI№ АII.
Учитывая выражение (4), уравнение первого начала термодинамики можно записать следующим образом:
dQ=dU+pdV.
Теплоемкостью системы тел (тела) называется физическая величина, равная отношению количества теплоты dQ, которое нужно затратить для нагревания системы тел (тела), к изменению температуры dТ, характеризующей это нагревание: 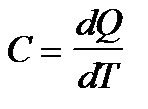 . [C]=Дж/К.
. [C]=Дж/К.
Удельной теплоемкостью вещества с называется скалярная величина, равная отношению теплоемкости однородного тела С к его массе: 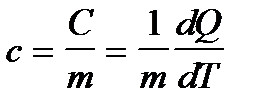
[c]= Дж/(кг.К)
Молярной теплоемкостью называется физическая величина, численно равная отношению теплоемкости системы С к количеству вещества n, содержащегося в ней: 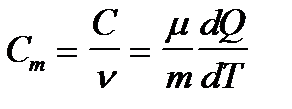 . [Cm]=Дж/(моль К)
. [Cm]=Дж/(моль К)
Различают молярные теплоемкости при постоянном объеме и постоянном давлении:
.
Уравнение, связывающее теплоемкости при постоянном давлении и постоянном объеме имеет вид (уравнение Майера): Cp – CV= R.
Учитывая распределение энергии по степеням свободы и уравнение Майера, получим распределение теплоемкостей Cp и CV по степеням свободы: 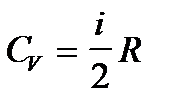 и
и 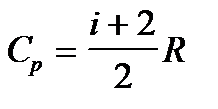 .
.
При рассмотрении термодинамических процессов удобно пользоваться соотношением: 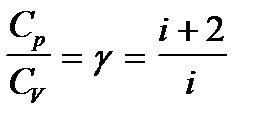 .
.
Величина g определяется числом и характером степеней свободы молекулы.
Для равновесных изопроцессов в газах уравнение первого начала термодинамики имеет вид: 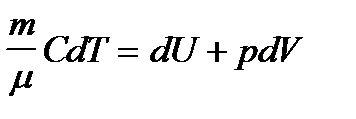 .
.
· Первое начало термодинамики при изохорическом процессе (V=const): 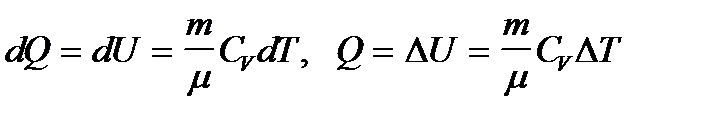
Здесь DТ=Т2–Т1 – разность температур конечного и начального состояний. При этом работа не совершается: 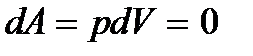
 · Первое начало термодинамики при изобарическом процессе (p=const):
· Первое начало термодинамики при изобарическом процессе (p=const): 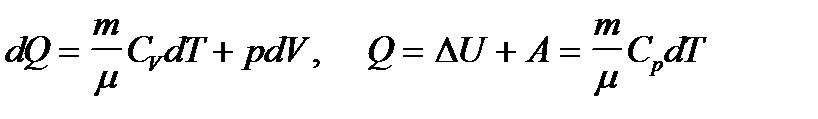 .
.
График изобарического процесса представлен на рис.41.1. Работа изобарного расширения равна площади фигуры, заштрихованной на рисунке и имеет значение
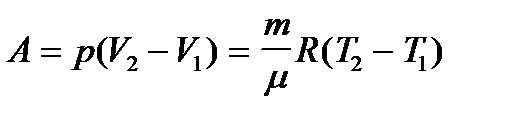 .
.
Здесь же мы сможем вывести уравнение Майера и сформулировать физический смысл универсальной газовой постоянной.
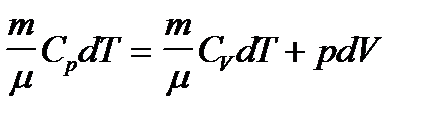 .
.
Для изобарического процесса (с учетом уравнения Менделеева-Клапейрона) 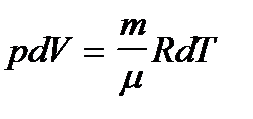 .
.
Поэтому 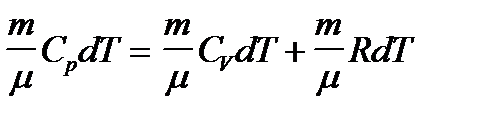 ,
,
или
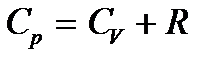 (уравнение Майера)
(уравнение Майера)
Универсальная газовая постоянная численноравна работе, которую необходимо совершить, чтобы нагреть 1 моль вещества на 1 К при постоянном давлении.
 · Первое начало термодинамики при изотермическом процессе (Т=const):
· Первое начало термодинамики при изотермическом процессе (Т=const): 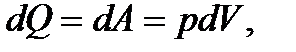 – теплота, сообщаемая системе при изотермическом процессе, идет на работу против внешних сил:
– теплота, сообщаемая системе при изотермическом процессе, идет на работу против внешних сил:
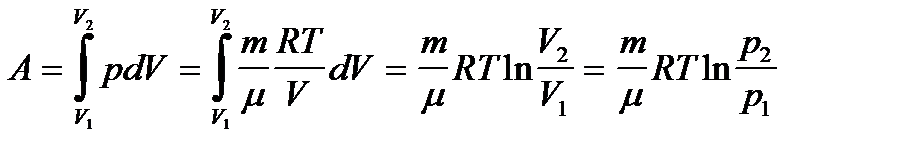
Итак, работа при изотермическом процессе:
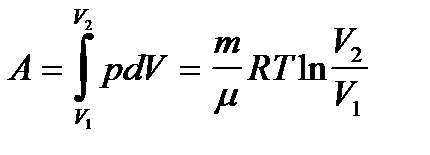 .
.
Изменение внутренней энергии dU=0, теплоемкость системы равна бесконечности.
Если газ изотермически расширяется (V2>V1), то к нему подводится тепло, и он совершает положительную работу, которая измеряется площадью, заштрихованной на рисунке фигуры. Если же газ изотермически сжимается (V2<V1), то он совершает отрицательную работу (то есть над ним совершают работу внешние силы).
Адиабатным называется процесс, протекающий без теплообмена с внешней средой: dQ=0, Q=0
Чтобы процесс был адиабатным, необходимо, чтобы система была отделена от окружающих тел теплонепроницаемой перегородкой, либо процесс должен быть очень быстро протекающим, причем настолько быстро, чтобы не успел установиться теплообмен.
Итак, для адиабатного процесса уравнение состояния: 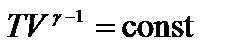 (1)
(1)
Из уравнения Менделеева-Клапейрона: T=pV/R.
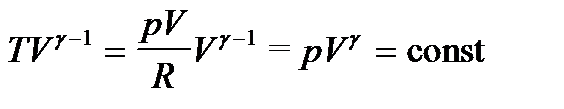 ; т.е.
; т.е. 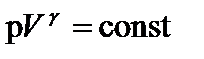 (2)
(2)
Из уравнения Менделеева-Клапейрона: V=RT/p.
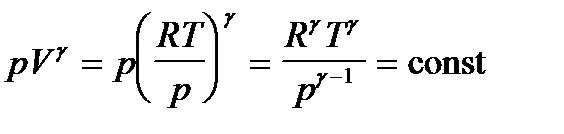 ;
; 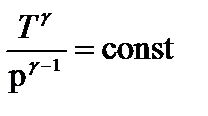 (3)
(3)
Уравнения (1), (2) и (3) – уравнения адиабатного процесса, названы уравнениями Пуассона.
 При сопоставлении адиабатного и изотермического процессов видно, что адиабата проходит более круто, чем изотерма: для изотермы pV = const, для адиабаты
При сопоставлении адиабатного и изотермического процессов видно, что адиабата проходит более круто, чем изотерма: для изотермы pV = const, для адиабаты 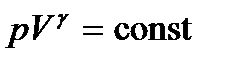 , а g>1, то есть давление при адиабатическом процессе зависит сильнее.
, а g>1, то есть давление при адиабатическом процессе зависит сильнее.
Объяснение этого факта с молекулярно-кинетической точки зрения: давление газа обусловлено ударами молекул о стенки сосуда. При изотермическом процессе изменяется число ударов молекул в единицу времени на единицу площади, а средняя сила ударов не изменяется. При адиабатном процессе изменяется и среднее число ударов в единицу времени, и средняя сила ударов.
Первое начало термодинамики не дает никаких указаний относительно направления, в котором могут происходить процессы в природе. С точки зрения первого начала любой мыслимый процесс, не противоречащий закону сохранения и превращения энергии, может быть реализован в природе. Например, если имеются два тела, температуры которых различны, то по первому началу термодинамики не противоречил бы переход теплоты от тела с более низкой температурой к телу с температурой более высокой. Единственным ограничением, налагаемым первым началом на этот процесс, является требование, чтобы количество теплоты, отданной одним телом, было равно количеству теплоты, полученной вторым.
О направлении процессов, происходящих в действительности, позволяет судить второе начало термодинамики. Оно совместно с первым началом позволяет также установить множество точных количественных соотношений между различными макроскопическими параметрами тел в состоянии термодинамического равновесия. Основоположником второго начала термодинамики считается французский инженер и физик Сади Карно. Он исследовал условия превращения теплоты в работу.
Чтобы прийти к формулировке второго начала термодинамики, рассмотрим схематически работу тепловой машины. В процессе работы она совершает многократный круговой процесс (цикл).
Круговой процесс – это совокупность термодинамических процессов, в результате которых система возвращается в исходное состояние. На диаграммах состояния круговые процессы изображаются замкнутыми линиями.
Изменение внутренней энергии равно 0: 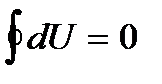 . Первое начало для круговых процессов имеет вид:
. Первое начало для круговых процессов имеет вид: 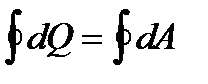 .
.
Прямым циклом называется круговой процесс, в котором система совершает положительную работу
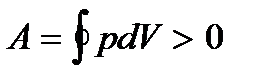 . Замкнутая кривая на диаграмме, изображающая прямой цикл, описывается по часовой стрелке. Для того, чтобы система совершала за цикл положительную работу, надо, чтобы расширение происходило при более высоких давлениях, чем сжатие.
. Замкнутая кривая на диаграмме, изображающая прямой цикл, описывается по часовой стрелке. Для того, чтобы система совершала за цикл положительную работу, надо, чтобы расширение происходило при более высоких давлениях, чем сжатие.
Пусть Q1 – количество теплоты, которое система получила при расширении (рис. 43.1); Q2 – система отдала при сжатии; U1– внутренняя энергия системы в первом состоянии, U2 – внутренняя энергия системы во втором состоянии.
При расширении рабочее вещество получает от нагревателя теплоту Q1 и совершает положительную работу А1. Согласно первому началу термодинамики: Q1=U2–U1 + A1.
При сжатии над рабочим веществом совершается работа А2 и при этом оно отдает холодильнику количество теплоты Q2: Q2=U1–U2 – A2
В результате: Q1– Q2=A1–A2
Таким образом, тепловая машина совершила прямой круговой цикл, в результате которого нагреватель отдал теплоту Q1, холодильник получил теплоту Q2. Теплота Q= Q1 – Q2 пошла на выполнение работы А=A1–A2.
В тепловой машине не вся получаемая извне теплота Q1 используется для совершения полезной работы. Поэтому тепловая машина характеризуется коэффициентом полезного действия. К.п.д.(h) — это отношение совершаемой за цикл работы А к получаемой за цикл теплоте:
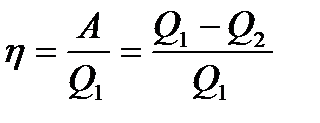 (1)
(1)
 Если при круговом процессе газ, расширяясь, совершает меньшую работу, чем та, которую производят внешние силы при егосжатии, т.е. А1<A2, то такой цикл носит название обратного. Он может совершаться в том случае, когда расширение газа происходит при более низкой температуре, чем сжатие. При этом газ отдает больше теплоты, чем получает при расширении. Машины, работающие по обратному циклу, носят название холодильных. В холодильных машинах процесс переноса теплоты от холодного тела к более горячему требует затраты работы внешних сил (А2–А1). На диаграмме обратный цикл изображается замкнутой кривой, проходимой против часовой стрелки. На рис. 43.2 схематически представлены принципы действия теплового двигателя и холодильной машины.
Если при круговом процессе газ, расширяясь, совершает меньшую работу, чем та, которую производят внешние силы при егосжатии, т.е. А1<A2, то такой цикл носит название обратного. Он может совершаться в том случае, когда расширение газа происходит при более низкой температуре, чем сжатие. При этом газ отдает больше теплоты, чем получает при расширении. Машины, работающие по обратному циклу, носят название холодильных. В холодильных машинах процесс переноса теплоты от холодного тела к более горячему требует затраты работы внешних сил (А2–А1). На диаграмме обратный цикл изображается замкнутой кривой, проходимой против часовой стрелки. На рис. 43.2 схематически представлены принципы действия теплового двигателя и холодильной машины.
Из формулы (1) предыдущего параграфа видно, что к.п.д. тепловой машины меньше единицы. Наилучшей была бы машина, с к.п.д., равным единице. Такая машина могла бы полностью превращать в работу всю полученную от некоторого тела теплоту, ничего не отдавая холодильнику. Многочисленные опыты показали невозможность создания подобной машины. К такому выводу впервые пришел Сади Карно в 1824 г. Изучив условия работы тепловых машин, он доказал, что для производства работы тепловой машиной нужно не менее двух источников теплоты с различными температурами. В дальнейшем это детально было изучено Р.Клаузиусом (1850 г.) и В.Кельвином (1852 г.), которые сформулировали второе начало термодинамики.
Формулировка Клаузиуса(1850): Тепло не может самопроизвольно переходить от менее нагретого к более нагретому телу без каких-либо изменений в системе. То есть, невозможен процесс, единственным конечным результатом которого является передача энергии в форме теплоты от менее нагретого тела к более нагретому.
Из этого определения не вытекает, что тепло не может передаваться от менее нагретого к более нагретому телу. Тепло передается от менее нагретого к более нагретому телу в любых холодильных установках, но передача тепла здесь не является конечным результатом, так как при этом совершается работа.
Формулировка Томсона (Кельвина) (1851): Невозможно преобразовать в работу всю теплоту, взятую от тела с однородной температурой, не производя никаких других изменений в состоянии системы. То есть, невозможен процесс, единственным конечным результатом которого является превращение всей теплоты, полученной от некоторого тела, в эквивалентную ей работу.
Здесь не вытекает, что теплота не может быть полностью обращена в работу. Например, при изотермическом процессе (dU=0) теплота полностью обращается в работу, но этот результат не является единственным, конечным, так как здесь еще происходит расширение газа.
Видно, что приведенные формулировки эквивалентны.
Второе начало термодинамики был окончательно сформулирован тогда, когда окончились неудачей все попытки создать двигатель, который бы обращал в работу всю полученную им теплоту, не вызывая при этом никаких других изменений состояния система - вечный двигатель второго рода. Это двигатель, имеющий к.п.д. 100%. Поэтому другая формулировка второго начала термодинамики: невозможен перпетуум-мобиле второго рода, т.е. такой периодически действующий двигатель, который получал бы тепло от одного резервуара и превращал эту теплоту полностью в работу.
Второе начало термодинамики позволяет разделить все термодинамические процессы на обратимые и необратимые. Если в результате какого-либо процесса система переходит из состояния А в другое состояние В и если возможно вернуть ее хотя бы одним способом в исходное состояние А и притом так, чтобы во всех остальных телах не произошло никаких изменений, то этот процесс называется обратимым. Если же это сделать невозможно, то процесс называется необратимым. Обратимый процесс можно было бы осуществить в том случае, если прямое и обратное направления его протекания были бы равновозможны и равноценны.
Обратимыми процессами являются процессы, протекающие с очень малой скоростью, в идеальном случае бесконечно медленно. В реальных условиях процессы протекают с конечной скоростью, и поэтому их можно считать обратимыми только с определенной точностью. Наоборот, необратимость является характерным свойством, вытекающим из самой природы тепловых процессов. Примером необратимых процессов являются все процессы, сопровождающиеся трением, процессы теплообмена при конечной разности температур, процессы растворения и диффузии. Эти все процессы в одном направлении протекают самопроизвольно, "сами собой", а для совершения каждого из этих процессов в обратном направлении необходимо, чтобы параллельно происходил какой-то другой, компенсирующий процесс. Следовательно, в земных условиях у событий имеется естественный ход, естественное направление.
Второе начало термодинамики определяет направление протекания термодинамических процессов и тем самым дает ответ на вопрос, какие процессы в природе могут протекать самопроизвольно. Оно указывает на необратимость процесса передачи одной формы энергии – работы в другую – теплоту. Работа – форма передачи энергии упорядоченного движения тела как целого; теплота – форма передачи энергии неупорядоченного хаотического движения. Упорядоченное движение может переходить в неупорядоченное самопроизвольно. Обратный переход возможен лишь при условии совершения работы внешними силами.
Анализируя работу тепловых двигателей, Карно пришел к выводу, что наивыгоднейшим процессом является обратимый круговой процесс, состоящий из двух изотерм и двух адиабат, так как он характеризуется наибольшим коэффициентом полезного действия. Такой цикл получил название цикла Карно.
Цикл Карно – прямой круговой процесс, при котором выполненная системой работа максимальна. Цикл состоит из двух изотермических (1®2 и 3®4) и двух адиабатических расширений и сжатий (2®3 и 4®1) (рис.45.1). Машина, совершающая цикл Карно, называется идеальной тепловой машиной.
Работа, совершаемая при изотермическом расширении: 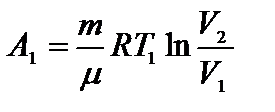 ; А1=Q1. (1)
; А1=Q1. (1)
При адиабатическом расширении работа совершается за счет убыли внутренней энергии системы, т.к. Q=0:
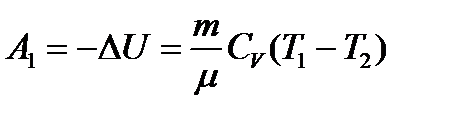 .
.
Работа, совершаемая над системой при изотермическом сжатии: 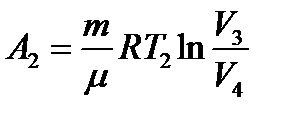 ; А2=Q2. (2)
; А2=Q2. (2)
Работа при адиабатическом сжатии: А2= –DU = 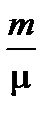 СV(Т2–Т1).
СV(Т2–Т1).
Подсчитаем КПД идеальной тепловой машины.
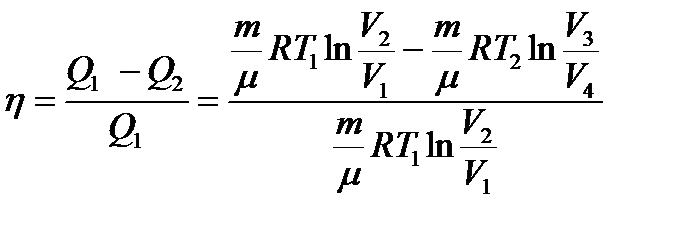 (3)
(3)
Запишем уравнения Пуассона для двух адиабатических процессов: 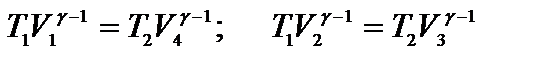
Взяв их отношение, получим: 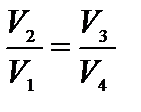 .
.
Выразив в формуле (3) 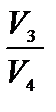 через
через 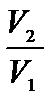 и сократив на
и сократив на 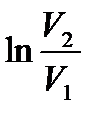 , получим:
, получим: 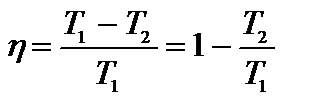 .
.
Отсюда сформулируем первую теорему Карно: коэффициент полезного действия обратимого цикла Карно не зависит от природы рабочего тела и является функцией только абсолютных температур нагревателя и холодильника.
Вторая теорема Карно: любая тепловая машина, работающая при данных значениях температур нагревателя и холодильника, не может иметь большего КПД, чем машина, работающая по обратимому циклу Карно при тех же значениях температур нагревателя и холодильника:
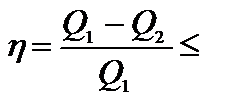
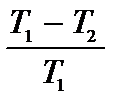 .
.
Термический КПД произвольного обратимого цикла 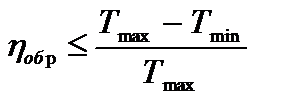
где Тmax и Tmin – экстремальные значения температуры нагревателя и холодильника, участвующих в осуществлении рассматриваемого цикла.
Понятие энтропии впервые было введено Р.Клаузиусом в 1862 году.
Функция состояния S, дифференциал которой: 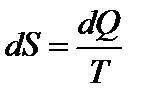 (2)
(2)
называется энтропией. Здесь dQ –бесконечно малое количество теплоты, сообщенное системе в элементарном обратимом процессе, Т – абсолютная температура системы. Интегрируя выражение (2), получим: 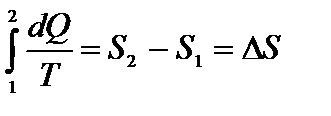 ,
,
где S1 и S2 – значения энтропии в состояниях 1 и 2, DS – изменение энтропии в течение обратимого процесса. Изменение энтропии в любом обратимом процессе, переводящем систему из состояния 1 в состояние 2, равно приведенному количеству теплоты, переданному системе в этом процессе.
Каждому состоянию тела соответствует одно определенное значение энтропии. Поэтому энтропия является однозначной функцией состояния. Физический смысл имеет не сама энтропия, а лишь разность энтропий. Клаузиусом были получены следующие важные положения, которые сформулируем без доказательства:
1. Энтропия является аддитивной величиной: энтропия системы из нескольких тел является суммой энтропий всех тел.
2. Энтропия определяется только с точностью до произвольной постоянной.
3. Если в изолированной системе происходят обратимые процессы, то ее энтропия остается неизменной: 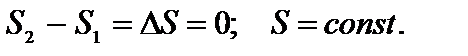
4. Энтропия изолированной системы при протекании необратимого процесса возрастает. Энтропия изолированной системы не может уменьшаться ни при каких процессах. Математически эти положения можно записать в виде неравенства называемогонеравенством Клаузиуса: 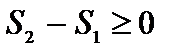 (3)
(3)
5. Энтропия системы, находящейся в равновесном состоянии, максимальна.
В природе все реальные процессы являются необратимыми. Поэтому можно утверждать, что все процессы в конечной изолированной системе ведут к увеличению энтропии. Это принцип возрастания энтропии. Основываясь на вышеизложенном, можно так сформулировать второе начало термодинамики: в изолированных системах возможны лишь такие процессы, при которых энтропия не убывает. Она постоянна, если процессы обратимы, и возрастает, если процессы необратимы.
Если система не изолирована, то ее энтропия может вести себя произвольным образом. Если система отдает тепло (DQ<0), то ее энтропия убывает. Если такая система совершает замкнутый цикл, то энтропия в конце цикла буде равна исходному значению, то есть ее изменение равно нулю. Однако на разных этапах энтропия может и убывать, и возрастать, но так, что сумма всех изменений энтропии равно нулю.
Тема 9. Молекулярно-кинетическая теория
В молекулярно-кинетической теории пользуются идеализированной модельюидеального газа, согласно которой считают, что:
1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;
2) между молекулами газа отсутствуют силы взаимодействия;
3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.
В газе молекулы большую часть времени находятся так далеко друг от друга, что силы взаимодействия между ними практически равны нулю. Можно считать, что кинетическая энергия молекул газа много больше потенциальной, поэтому последней можно пренебречь.
В молекулярной физике и термодинамике состояние газа характеризуется совокупностью трех макропараметров р, V, Т , которые называются параметрами состояния.
Температура — одно из основных понятий, играющих важную роль не только в термодинамике, но и в физике в целом.Температура — физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы. В соответствии с решением XI Генеральной конференции по мерам и весам (1960) в настоящее время можно применять только две температурные шкалы —термодинамическую и Международную практическую, градуированные соответственно в кельвинах (К) и в градусах Цельсия (°С). ВМеждународной практической шкале температура замерзания и кипения воды при давлении 1,013 10s Па соответственно О и 100°С(репервые точки).
Давление в системе СИ измеряется в Па (паскаль): 1Н/м2=1 Па. Часто пользуются и внесистемными единицами давления: 1 мм рт. ст.=133,3 Па; техническая атмосфера 1 ат = 750 мм рт. ст. » 105Па; нормальная (физическая) атмосфера: 1атм=760мм рт.ст.»1,013. 105Па.
Основным уравнением кинетической теории газов называется соотношение, связывающее давление (величину, измеряемую на опыте) со скоростью или кинетической энергией молекулы газа.
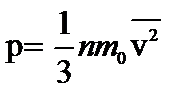 (3)
(3)
Данное выражение называется основным уравнением молекулярно-кинетической теории идеальных газов. Это уравнение как раз и устанавливает связь между давлением и скоростью, вернее среднеквадратичной скоростью.
Введем 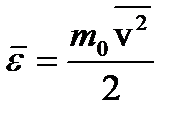 – среднюю кинетическую энергию хаотического поступательного движения одной молекулы, тогда основное уравнение запишется как:
– среднюю кинетическую энергию хаотического поступательного движения одной молекулы, тогда основное уравнение запишется как: 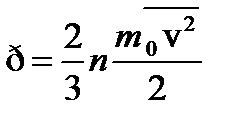 или
или 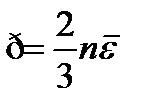
В данном уравнении давление связано со средней энергией поступательного движения молекул. Давление газа численно равно 2/3 средней кинетической энергии поступательного движения молекул, содержащихся в единице объема.
Давление идеального газа связано с температурой соотношением: 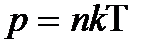 .
.
Давление определяется только концентрацией (при постоянной температуре) и не зависит от сорта молекул.
Если имеем смесь нескольких газов, концентрация молекул которых n1, n2, ..., ni и 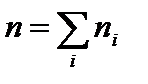 , то
, то 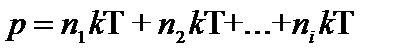 .
.
Давления 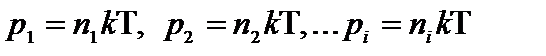 называют парциальными давлениями. Например, р1 – парциальное давление соответствует давлению, которое оказывал бы первый газ, входящий в состав смеси, если бы он занимал весь объем.
называют парциальными давлениями. Например, р1 – парциальное давление соответствует давлению, которое оказывал бы первый газ, входящий в состав смеси, если бы он занимал весь объем.
Согласно закону Дальтона в случае идеальных газов 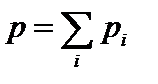 .
.
Таким образом, давление, оказываемое на стенки сосуда смесью газов, равно сумме парциальных давлений отдельных компонентов смеси.
Дата добавления: 2016-10-26; просмотров: 3542;











