Элементы специальной теории относительности и механики сплошных сред

Тема 6. Основы специальной теории относительности

Классическая механика Ньютона достоверно описывает движение макроскопических тел, движущихся со скоростями, намного меньшими скорости света. В конце XIX в. было установлено, что выводы классической механики противоречат некоторым опытным данным. В частности при изучении движения быстрых заряженных частиц оказалось, что их движение не подчиняется законам Ньютона. Далее возникли затруднения при попытках применить классическую механику для объяснения распространения света. Согласно законам электродинамики скорость распространения электромагнитных волн в вакууме одинакова по всем направлениям и приблизительно равна с = 3·10⁸ м/с. Но в соответствии с законами классической физики скорость света может равняться с только в одной избранной системе отсчета. В любой другой системе отсчета, движущейся относительно избранной системы со скоростью v, она должна уже равняться c-v, или c+v. Это означает, что если справедлив закон сложения скоростей классической механики (формула (5.4)), то при переходе от одной инерциальной системы к другой законы электродинамики должны меняться, так как должна меняться скорость света. Таким образом, обнаружились противоречия между электродинамикой и механикой Ньютона, законы которой согласуются с принципом относительности Галилея.

Последовательно развивая новые, отличные от классических, представления о пространстве и времени, А. Эйнштейн в начале XX в. создал специальную теорию относительности (СТО). В рамках этой теории удалось согласовать принцип относительности с электродинамикой Максвелла. При этом новая теория не отменяла старую (ньютоновскую механику), а включала ее в себя как частный, предельный случай.

Специальная теория относительности представляет собой современную физическую теорию пространства и времени. В СТО, как и в классической механике, предполагается, что время однородно (инвариантность физических законов относительно выбора начала отсчета времени), а пространство однородно и изотропно (симметрично). Специальная теория относительности называется также релятивистской теорией, а явления, описываемые этой теорией – релятивистскими эффектами.

В основу СТО легло положение, согласно которому никакая энергия, никакой сигнал не могут распространяться со скоростью, превышающей скорость света в вакууме, а скорость света в вакууме постоянна и не зависит от направления распространения.

Это положение формулируется в виде двух постулатов А. Эйнштейна: принципа относительности и принципа постоянства скорости света.

Первый постулат является обобщением механического принципа относительности Галилея на любые физические процессы и утверждает, что законы физики имеют одинаковую форму (инвариантны) во всех инерциальных системах отсчета: любой процесс протекает одинаково в изолированной материальной системе, находящейся в состоянии покоя, и в такой же системе, находящейся в состоянии равномерного прямолинейного движения. Состояние покоя или движения определяется здесь относительно произвольно выбранной инерциальной системы отсчета; физически эти состояния равноправны.

Второй постулат утверждает: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета.

.

K

K΄

y

z

x

v

A

z΄

x΄

y΄

0΄

Рис. 5.2

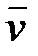Рассмотрим две инерциальные системы отсчета: К (с координатами x, y, z) и К΄ (с координатами x΄, y΄, z΄), движущуюся относительно К вдоль оси х со скоростью =const. Пусть в начальный момент времени (t = t΄ = 0), когда начала систем координат совпадают (0 = 0΄), излучается световой импульс. Согласно второму постулату Эйнштейна скорость света в обеих системах одна и та же и равна с. Поэтому если за время t в системе К сигнал дойдет до некоторой точки А, пройдя расстояние

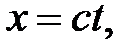(5.6)

то в системе К΄ координата светового импульса в момент достижения точки А будет равна

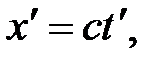(5.7)

где t΄ - время прохождения светового импульса от начала координат до точки А в системе К΄. Вычитая (5.6) из (5.7), получим: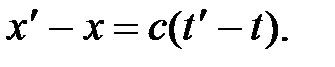

Так как 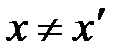(система К΄ перемещается относительно К), то получается, что 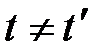, т.е. отсчет времени в системах К΄ и К различен или имеет относительный характер (в классической механике считается, что время во всех инерциальных системах отсчета протекает одинаково, т.е. t = t΄).

А. Эйнштейн показал, что в СТО классические преобразования Галилея при переходе от одной инерциальной системы отсчета к другой заменяются преобразованиями Лоренца (1904 г.), удовлетворяющими первому и второму постулатам (табл. 5.1).

Таблица 5.1

Прямые	преобразования	Обратные	преобразования
Галилея	Лоренца	Галилея	Лоренца

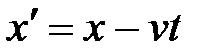
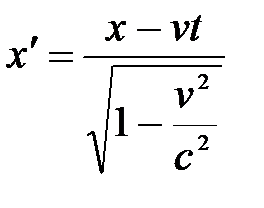
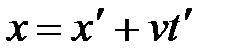
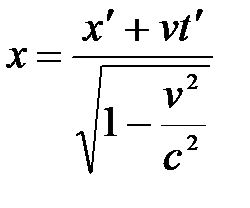
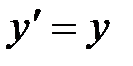
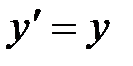
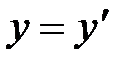
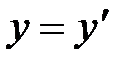
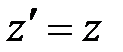
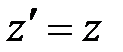
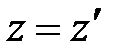
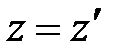
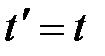
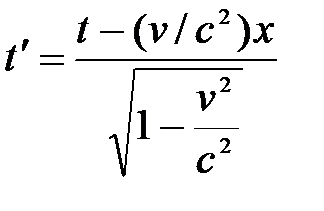
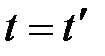
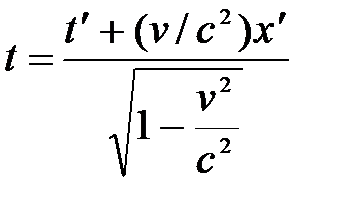
Из преобразований Лоренца вытекает, что при малых скоростях (по сравнению со скоростью света) они переходят в преобразования Галилея. При v>c выражения для x, t, x΄ и t΄ теряют физический смысл, т.е. движение со скоростью, большей скорости света в вакууме, невозможно.

Следствия из преобразований Лоренца

1. Относительность одновременности. Пусть в системе К в точках с координатами х₁ и х₂ в моменты времени t₁ и t₂ происходят два события. В системе К΄ им соответствуют координаты 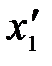и 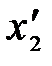и моменты времен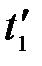и и . Если события в системе К происходят в одной точке (х₁=х₂) и являются одновременными (t₁=t₂), то, согласно преобразованиям Лоренца,

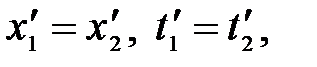
т.е. эти события являются одновременными и пространственно совпадающими для любой инерциальной системы отсчета.

Если события в системе К пространственно разобщены (х₁ ≠ х₂), но одновременны (t₁=t₂), то в системе К΄, согласно преобразованиям Лоренца,

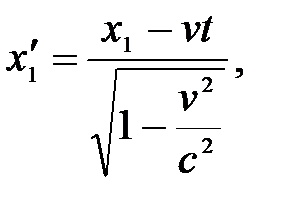
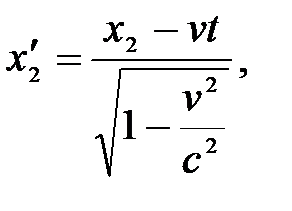
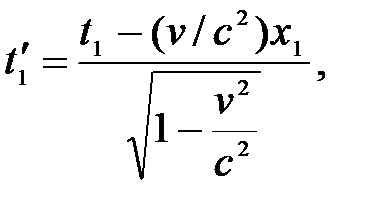
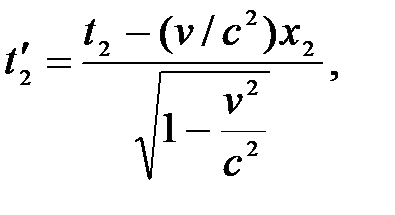
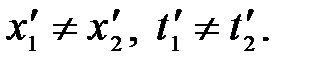
Таким образом, в системе К΄ эти события, оставаясь пространственно разобщенными, оказываются и неодновременными.

2. Длительность событий в разных системах отсчета. Пусть в некоторой точке А с координатой х, покоящейся относительно системы К, происходит событие, длительность которого (разность показаний часов в конце и начале события) 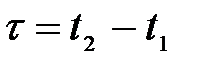, где индексы 1 и 2 соответствуют началу и концу события. Длительность этого же события в системе К΄

,

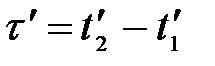где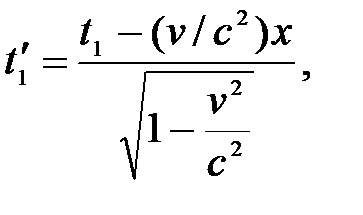

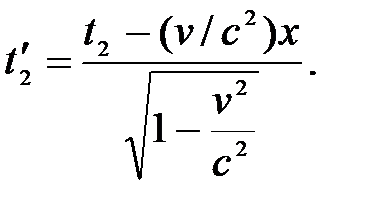
Таким образом, 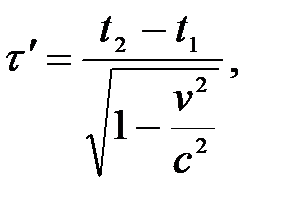или ,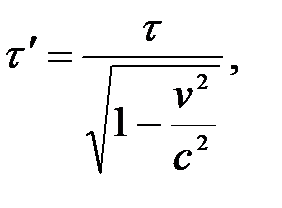

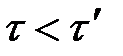т.е. длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна. Следовательно, часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов, т.е. ход часов замедляется в системе отсчета, относительно которой часы движутся.

3. Длина тел в разных системах отсчета. Рассмотрим стержень, расположенный вдоль оси x΄ и покоящийся относительно системы К΄. Длина стержня в системе К΄ равна 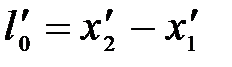, где 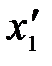, 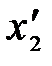- не изменяющиеся со временем t΄ координаты начала и конца стержня; индекс 0 показывает, что в системе К΄ стержень покоится. Определим длину стержня в системе К, относительно которой он движется со скоростью v. Для этого необходимо измерить координаты концов стержня х₁ и х₂ в системе К в один и тот же момент времени t. Их разность 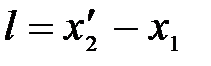и даст длину стержня в системе К:

-

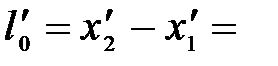
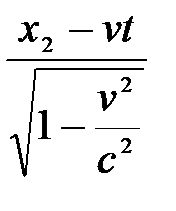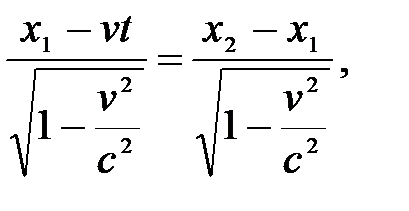
т.е.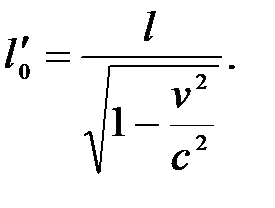

Таким образом, размер тела, движущегося относительно инерциальной системы отсчета, уменьшается в направлении движения в 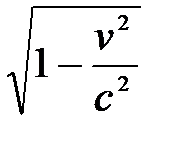раз, т.е. лоренцево сокращение длины тем больше, чем больше скорость движения.

4. Релятивистский закон сложения скоростей. Пусть материальная точка движется в системе К΄ вдоль оси x΄, а система К΄ движется относительно К со скоростью v (оси х и x΄ совпадают). Тогда

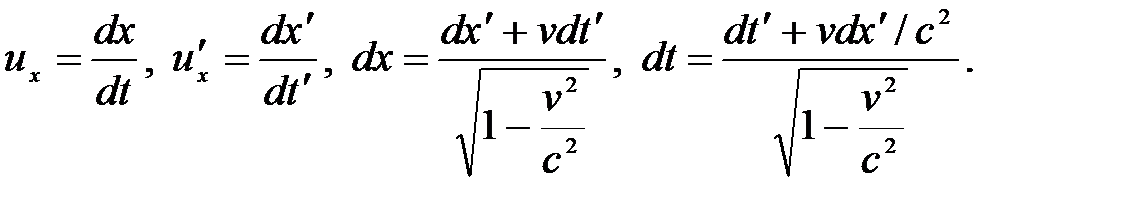
Произведя вычисления, получим релятивистский закон сложения скоростей:

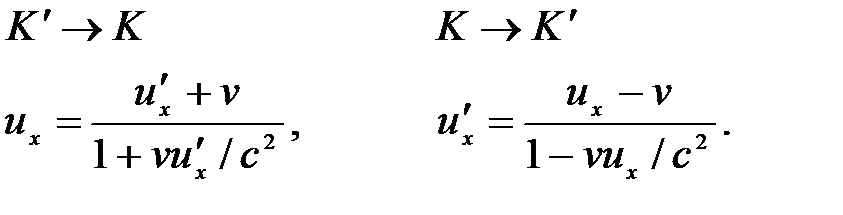
Если скорости v, 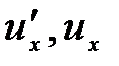малы по сравнению со скоростью света, то эти формулы переходят в привычный закон сложения скоростей в классической механике. Релятивистский закон сложения скоростей не противоречит второму постулату Эйнштейна: если 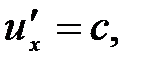то 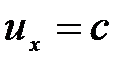, т.е. скорость с – предельная скорость, которую невозможно превысить.

Согласно представлениям классической механики, масса тела есть величина постоянная. Однако в конце XIX в. на опытах с электронами было установлено, что масса тела зависит от скорости его движения, а именно возрастает с увеличением v по закону

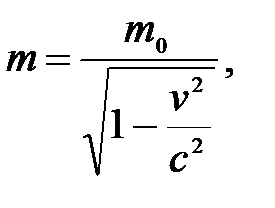(5.8)

где 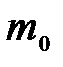- масса покоя, т.е. масса материальной точки, измеренная в той инерциальной системе отсчета, относительно которой точка покоится; m – масса точки в системе отсчета, относительно которой она движется со скоростью v.

Из принципа относительности Эйнштейна, утверждающего инвариантность всех законов природы при переходе от одной инерциальной системы отсчета к другой, следует, что основной закон динамики Ньютона

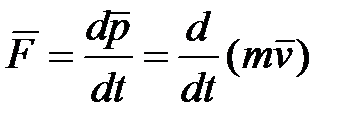
оказывается инвариантным по отношению к преобразованиям Лоренца, если в нем справа стоит производная от релятивистского импульса:

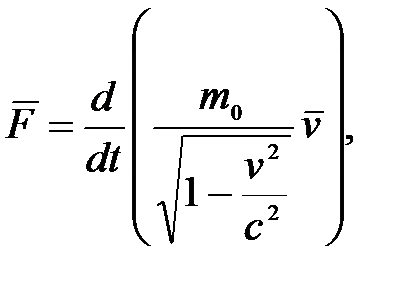(5.9)

или

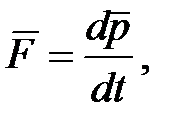(5.10)

где

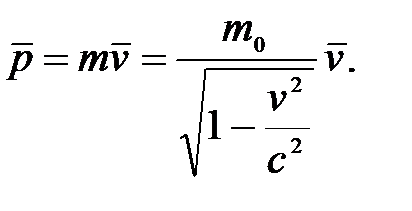(5.11)

Из приведенных формул следует, что при скоростях, значительно меньших скорости света в вакууме, они переходят в формулы классической механики. Следовательно, условием применимости законов классической механики является условие 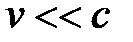. Законы Ньютона получаются как следствие СТО для предельного случая . Таким образом, классическая механика – это механика макротел, движущихся с малыми (по сравнению со скоростью света в вакууме) скоростями.

Вследствие однородности пространства в релятивистской механике выполняется закон сохранения релятивистского импульса: релятивистский импульс замкнутой системы тел сохраняется, т.е. не изменяется с течением времени.

Изменение скорости тела в релятивистской механике влечет за собой изменение массы, а, следовательно, и полной энергии, т.е. между массой и энергией существует взаимосвязь. Эту универсальную зависимость – закон взаимосвязи массы и энергии – установил А. Эйнштейн:

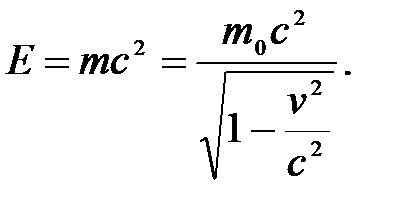(5.13)

Из (5.13) следует, что любой массе (движущейся m или покоящейся 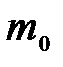) соответствует определенное значение энергии. Если тело находится в состоянии покоя, то его энергия покоя

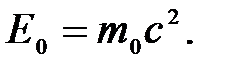
Энергия покоя является внутренней энергией тела, которая складывается из кинетических энергий всех частиц, потенциальной энергии их взаимодействия и суммы энергий покоя всех частиц.

В релятивистской механике не справедлив закон сохранения массы покоя. Именно на этом представлении основано объяснение дефекта массы ядра и ядерных реакций.

В СТО выполняется закон сохранения релятивистской массы и энергии: изменение полной энергии тела (или системы) сопровождается эквивалентным изменением его массы:

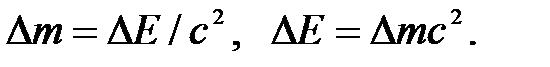(5.14)

Таким образом, масса тела, которая в классической механике является мерой инертности или гравитации, в релятивистской механике является еще и мерой энергосодержания тела.

Физический смысл выражения (5.14) состоит в том, что существует принципиальная возможность перехода материальных объектов, имеющих массу покоя, в электромагнитное излучение, не имеющее массы покоя; при этом выполняется закон сохранения энергии.

В релятивистской динамике значение кинетической энергии Е_к определяется как разность энергий движущегося Е и покоящегося Е₀ тела:

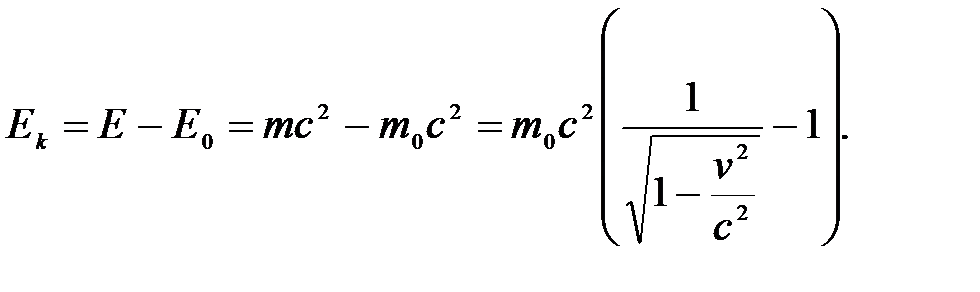(5.15)

При уравнение (5.15) переходит в классическое выражение

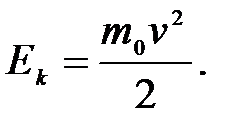
Из формул (5.13) и (5.11) найдем релятивистское соотношение между полной энергией и импульсом тела:

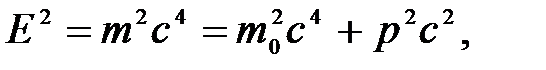
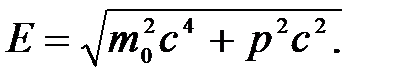(5.16)

Закон взаимосвязи массы и энергии полностью подтвержден экспериментами по выделению энергии при протекании ядерных реакций. Он широко используется для расчета энергического эффекта при ядерных реакциях и превращениях элементарных частиц