Кинематика поступательного движения
| . |
| z |
| x |
| y |
| x |
| z |
| y |
| A |
| Рис. 1.1 |
| r |
Положение материальной точки в пространстве в данный момент времени определяется по отношению к какому-либо другому телу, которое называется телом отсчета. С ним связывается система отсчета – совокупность системы координат и часов, связанных с телом, по отношению к которому изучается движение каких-нибудь других материальных точек. В декартовой системе координат положение точки А в данный момент времени по отношению к этой системе определяется тремя координатами х, у и z, или радиусом-вектором 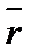 (рис. 1.1). При движении материальной точки ее координаты с течением времени изменяются. В общем случае ее движение определяется уравнениями
(рис. 1.1). При движении материальной точки ее координаты с течением времени изменяются. В общем случае ее движение определяется уравнениями
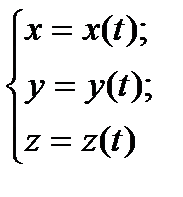 (1.1)
(1.1)
или векторным уравнением 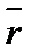 =
= 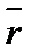 (t). (1.2)
(t). (1.2)
Эти уравнения называются кинематическими уравнениями движения материальной точки.
Траекторией движения материальной точки называется линия, описываемая этой точкой в пространстве. В зависимости от формы траектории движение может быть прямолинейным и криволинейным.
| . |
| . |
| z |
| x |
| y |
| A |
| B |
| r |
| r0 |
| Δr |
| Δs |
| Рис. 1.2 |
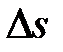 и является скалярной функцией времени
и является скалярной функцией времени 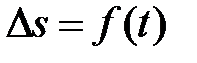 . Вектор
. Вектор 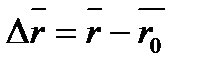 , проведенный из начального положения движущейся точки в положение ее в данный момент времени, называется вектором перемещения. При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и его модуль
, проведенный из начального положения движущейся точки в положение ее в данный момент времени, называется вектором перемещения. При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и его модуль 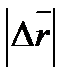 равен пройденному пути
равен пройденному пути 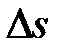 .
.
Скорость – это векторная физическая величина, введенная для определения быстроты движения и его направления в данный момент времени.
Вектором средней скорости 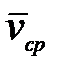 называется отношение приращения
называется отношение приращения 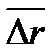 радиуса-вектора точки к промежутку времени
радиуса-вектора точки к промежутку времени  :
: 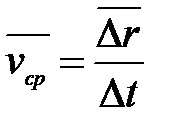 (1.3)
(1.3)
Вектор 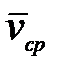 направлен так же, как
направлен так же, как 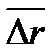 . При неограниченном уменьшении
. При неограниченном уменьшении  , средняя скорость стремится к предельному значению, которое называется мгновенной скоростью или просто скоростью:
, средняя скорость стремится к предельному значению, которое называется мгновенной скоростью или просто скоростью: 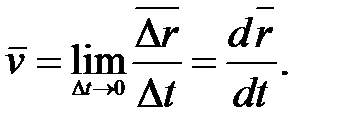 (1.4)
(1.4)
Таким образом, скорость – это векторная величина, равная первой производной радиуса-вектора движущейся точки по времени. Так как секущая в пределе совпадает с касательной, то вектор скорости 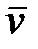 направлен по касательной к траектории в сторону движения.
направлен по касательной к траектории в сторону движения.
Если направление вектора мгновенной скорости 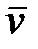 во время движения материальной точки не изменяется, это означает, что точка движется по траектории, касательные к которой во всех точках имеют одно и то же направление. Таким свойством обладают только прямолинейные траектории. Значит, рассматриваемое движение будет прямолинейным.
во время движения материальной точки не изменяется, это означает, что точка движется по траектории, касательные к которой во всех точках имеют одно и то же направление. Таким свойством обладают только прямолинейные траектории. Значит, рассматриваемое движение будет прямолинейным.
Если направление вектора скорости 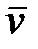 материальной точки изменяется с течением времени, точка будет описывать криволинейную траекторию.
материальной точки изменяется с течением времени, точка будет описывать криволинейную траекторию.
Если численное значение мгновенной скорости точки остается во время движения постоянным, то такое движение называется равномерным. Если за произвольные равные промежутки времени точка проходит пути разной длины, то численное значение ее скорости с течением времени изменяется. Такое движение называется неравномерным.
В природе чаще всего наблюдаются движения, в которых скорость изменяется как по величине (модулю), так и по направлению, т.е. приходится иметь дело с неравномерными движениями. Для характеристики изменения скорости таких движений вводится понятие ускорения.
| . |
| . |
| А |
| В |
| Δs |
| C |
| D |
| E |
| v |
| Δvτ |
| Δv |
| Δvn |
| v1 |
| Рис. 1.4 |
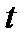 до
до 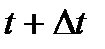 называется векторная величина, равная отношению изменения скорости
называется векторная величина, равная отношению изменения скорости 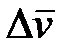 к интервалу времени
к интервалу времени  :
:
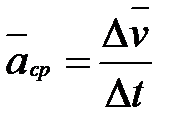 (1.9)
(1.9)
Очевидно, что вектор 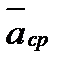 совпадает по направлению с вектором изменения скорости
совпадает по направлению с вектором изменения скорости 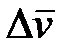 .
.
Мгновенным ускорением или ускорением материальной точки в момент времени 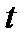 будет предел среднего ускорения:
будет предел среднего ускорения:
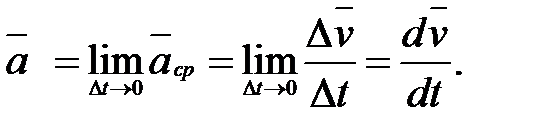 (1.10)
(1.10)
Таким образом, ускорение есть векторная величина, равная первой производной скорости по времени.
Составляющая ускорения, определяющая изменение скорости по величине, называется тангенциальной составляющей 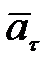 . Численно она равна первой производной по времени от модуля скорости:
. Численно она равна первой производной по времени от модуля скорости:
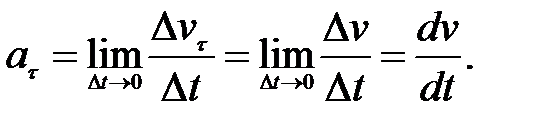 (1.11)
(1.11)
Найдем вторую составляющую ускорения, называемую нормальной составляющей.
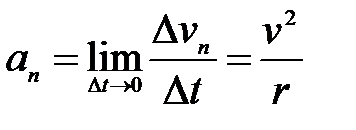 . (1.12)
. (1.12)
Она характеризует быстроту изменения скорости по направлению и направлена к центру кривизны траектории по нормали. Ее называют также центростремительным ускорением.
| aτ |
| v |
| a |
| an |
| φ |
| . |
| Рис. 1.5 |
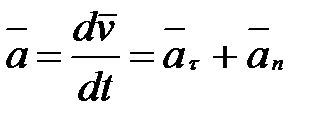 . (1.13)
. (1.13)
Из рис. 1.5 следует, что модуль полного ускорения равен:
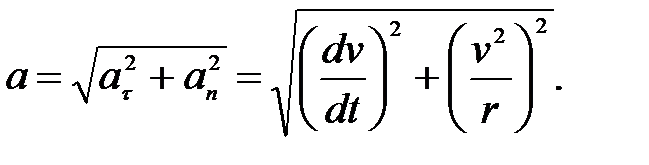 (1.14)
(1.14)
В зависимости от значений тангенциальной и нормальной составляющих ускорения движение тела классифицируется по-разному. Если 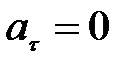 (величина скорости не изменяется по величине), движение является равномерным. Если
(величина скорости не изменяется по величине), движение является равномерным. Если 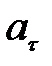 > 0, движение называется ускоренным, если
> 0, движение называется ускоренным, если  < 0 – замедленным. Если
< 0 – замедленным. Если 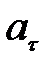 = const
= const 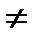 0, то движение называется равнопеременным. Наконец, в любом прямолинейном движении
0, то движение называется равнопеременным. Наконец, в любом прямолинейном движении 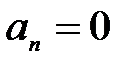 (нет изменения направления скорости).
(нет изменения направления скорости).
Таким образом, движение материальной точки может быть следующих видов:
1) 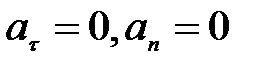 - прямолинейное равномерное движение (
- прямолинейное равномерное движение ( 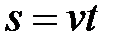 );
);
2) 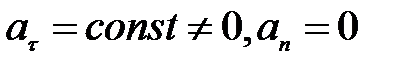 - прямолинейное равнопеременное движение.
- прямолинейное равнопеременное движение.
3)  - прямолинейное движение с переменным ускорением;
- прямолинейное движение с переменным ускорением;
4) 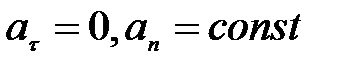 - скорость по модулю не изменяется,
- скорость по модулю не изменяется, 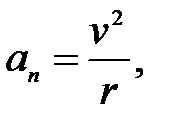 откуда видно, что радиус кривизны должен быть постоянным. Следовательно, данное движение по окружности является равномерным;
откуда видно, что радиус кривизны должен быть постоянным. Следовательно, данное движение по окружности является равномерным;
5) 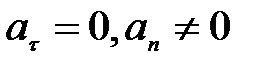 - равномерное криволинейное движение;
- равномерное криволинейное движение;
6) 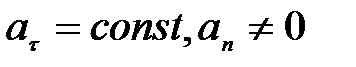 - криволинейное равнопеременное движение;
- криволинейное равнопеременное движение;
7) 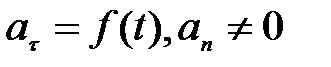 - криволинейное движение с переменным ускорением
- криволинейное движение с переменным ускорением
 Если системы отсчета движутся относительно друг друга равномерно и прямолинейно и в одной из них справедливы законы динамики Ньютона, то эти системы являются инерциальными. Во всех инерциальных системах отсчета законы классической динамики имеют одинаковую форму (инвариантны); в этом состоит суть механического принципа относительности или принципа относительности Галилея.
Если системы отсчета движутся относительно друг друга равномерно и прямолинейно и в одной из них справедливы законы динамики Ньютона, то эти системы являются инерциальными. Во всех инерциальных системах отсчета законы классической динамики имеют одинаковую форму (инвариантны); в этом состоит суть механического принципа относительности или принципа относительности Галилея.
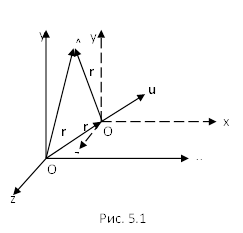
Для доказательства этого принципа рассмотрим две системы отсчета: инерциальную систему К (с координатами x, y, z), которую условно будем считать неподвижной и подвижную систему 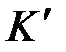 (с координатами
(с координатами 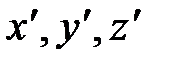 ), движущуюся относительно К равномерно и прямолинейно со скоростью
), движущуюся относительно К равномерно и прямолинейно со скоростью  = const. Примем, что в начальный момент времени t = 0 начала О и
= const. Примем, что в начальный момент времени t = 0 начала О и 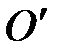 обеих систем координат совпадают. Расположение систем координат в произвольный момент времени t имеет вид, изображенный на рис. 5.1. Скорость
обеих систем координат совпадают. Расположение систем координат в произвольный момент времени t имеет вид, изображенный на рис. 5.1. Скорость  направлена вдоль прямой
направлена вдоль прямой  , а радиус-вектор, проведенный из точки О в точку
, а радиус-вектор, проведенный из точки О в точку 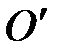 , равен
, равен 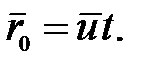
Координаты произвольной материальной точки А в неподвижной и подвижной системах отсчета определяются радиусами-векторами 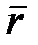 и
и  , причем
, причем
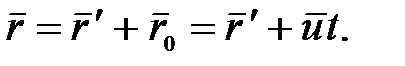 (5.1)
(5.1)
В проекциях на оси координат векторное уравнение (5.1) записывается в виде, называемом преобразованиями Галилея:
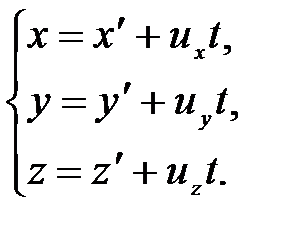 (5.2)
(5.2)
В частном случае, когда система 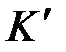 движется со скоростью
движется со скоростью 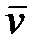 вдоль положительного направления оси х системы К, преобразования координат Галилея имеют следующий вид:
вдоль положительного направления оси х системы К, преобразования координат Галилея имеют следующий вид:
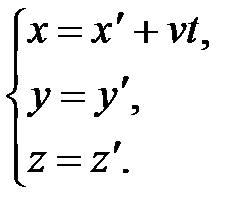
В классической механике предполагается, что ход времени не зависит от относительного движения систем отсчета. Поэтому система уравнений (5.2) дополняется еще одним соотношением:
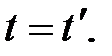 (5.3)
(5.3)
Соотношения (5.2) – (5.3) справедливы лишь в случае  . При скоростях, сравнимых со скоростью света, преобразования Галилея заменяются более общими преобразованиями Лоренца.
. При скоростях, сравнимых со скоростью света, преобразования Галилея заменяются более общими преобразованиями Лоренца.
Продифференцируем уравнение (5.1) по времени и учитывая, что  =const, найдем соотношения между скоростями и ускорениями точки А относительно обеих систем отсчета:
=const, найдем соотношения между скоростями и ускорениями точки А относительно обеих систем отсчета:
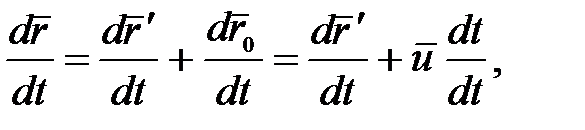
откуда
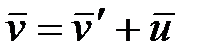 , (5.4)
, (5.4)
а также
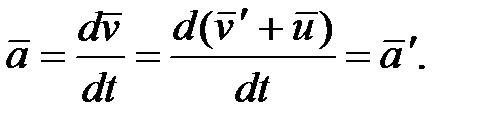 (5.5)
(5.5)
Если на точку А другие тела не действуют, то 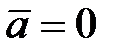 и согласно (5.5)
и согласно (5.5) 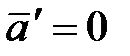 , т.е. подвижная система К΄ является инерциальной – изолированная материальная точка либо движется относительно нее равномерно и прямолинейно, либо покоится.
, т.е. подвижная система К΄ является инерциальной – изолированная материальная точка либо движется относительно нее равномерно и прямолинейно, либо покоится.
Из выражения (5.5) следует, что
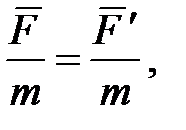 или
или 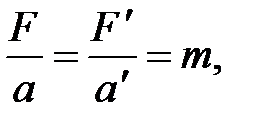
т.е. уравнения Ньютона (уравнения динамики) для материальной точки одинаковы во всех инерциальных системах отсчета или инвариантны по отношению к преобразованиям Галилея. Этот результат часто формулируют следующим образом: равномерное и прямолинейное движение системы как целого не влияет на ход протекающих в ней механических процессов.
Тема 2. Кинематика вращательного движения
| . |
| v |
| A |
| Δφ |
| R |
| dφ |
| ω |
| Рис. 1.6 |
Рассмотрим твердое тело, которое вращается вокруг неподвижной оси (рис. 1.6).Тогда отдельные точки этого тела будут описывать окружности разных радиусов, центры которых лежат на оси вращения. Пусть некоторая точка А движется по окружности радиуса R. Ее положение через промежуток времени  зададим углом
зададим углом 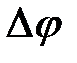 .
.
Угловой скоростью вращения называется вектор, численно равный первой производной угла поворота тела по времени и направленный вдоль оси вращения по правилу правого винта:
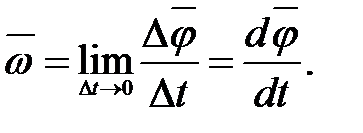 (1.18)
(1.18)
Единица измерения угловой скорости радиан в секунду (рад/с).
Таким образом, вектор 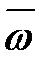 определяет направление и быстроту вращения. Если
определяет направление и быстроту вращения. Если 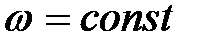 , то вращение называется равномерным.
, то вращение называется равномерным.
Угловая скорость может быть связана с линейной скоростью 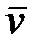 произвольной точки А. Пусть за время
произвольной точки А. Пусть за время  точка проходит по дуге окружности длину пути
точка проходит по дуге окружности длину пути 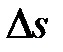 . Тогда линейная скорость точки будет равна:
. Тогда линейная скорость точки будет равна:
 (1.19)
(1.19)
При равномерном вращении его можно охарактеризовать периодом вращения Т – временем, за которое точка тела совершает один полный оборот, т.е. поворачивается на угол 2π:
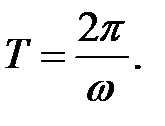
Число полных оборотов, совершаемых телом при равномерном движении по окружности, в единицу времени называется частотой вращения:
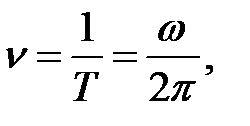
откуда 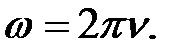
| ε |
| ω0 |
| ω |
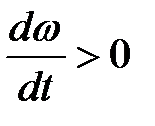
|
| ω |
| ω0 |
| ε |
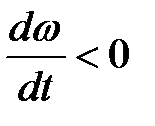
|
| Рис. 1.7 |
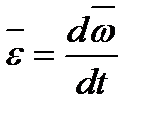 (1.20)
(1.20)
При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора угловой скорости (рис. 1.7); при ускоренном движении вектор 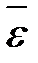 направлен в ту же сторону, что и
направлен в ту же сторону, что и 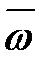
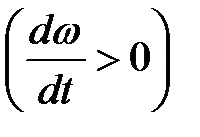 , и в противоположную сторону при замедленном вращении
, и в противоположную сторону при замедленном вращении 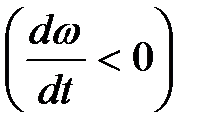 .
.
Выразим тангенциальную и нормальную составляющие ускорения точки А вращающегося тела через угловую скорость и угловое ускорение:
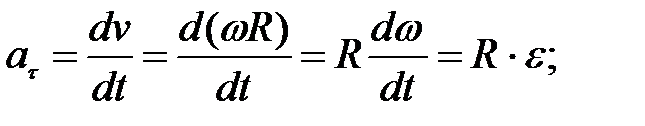 (1.21)
(1.21)
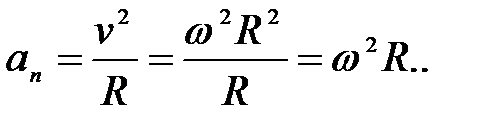 (1.22)
(1.22)
В случае равнопеременного движения точки по окружности ( 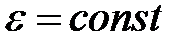 ):
):
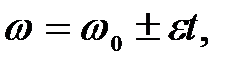
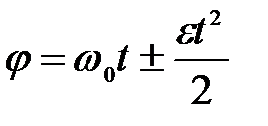 ,
,
где 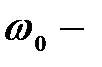 начальная угловая скорость.
начальная угловая скорость.
Поступательное и вращательное движения твердого тела являются лишь простейшими типами его движения. В общем случае движение твердого тела может быть весьма сложным. Однако в теоретической механике доказывается, что любое сложное движение твердого тела можно представить как совокупность поступательного и вращательного движений.
Кинематические уравнения поступательного и вращательного движений сведены в табл. 1.1.
Таблица 1.1
| Поступательное | Вращательное |
| Равномерное | |
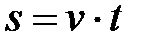
| 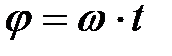
|
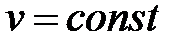
| 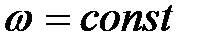
|
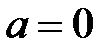
| 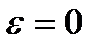
|
| Равнопеременное | |
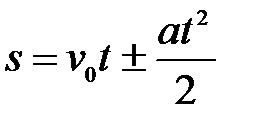
| 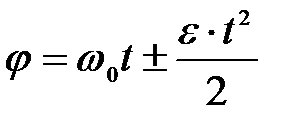
|
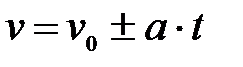
| 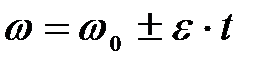
|
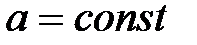
| 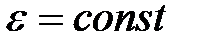
|
| Неравномерное | |
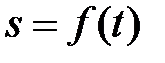
| 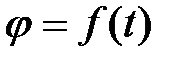
|

| 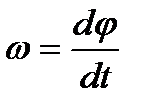
|
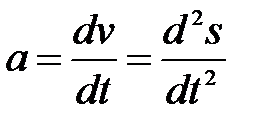
| 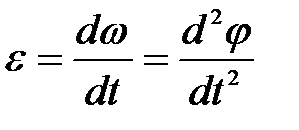
|
Тема 3. Динамика поступательного движения
Как уже отмечалось, динамика – это раздел классической механики, изучающий движение материальных тел под действием приложенных к ним сил, т.е. дающий связь между взаимодействиями тел и изменениями в их движении. Она является основным разделом механики и базируется на трех законах Ньютона (1687 г.)
Первый закон Ньютона (закон инерции) формулируется следующим образом: всякое тело (материальная точка) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит его изменить это состояние.
Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при отсутствии или взаимном уравновешивании внешних воздействий называется инертностью. Если на тело действует неуравновешенная система сил, то инертность сказывается в том, что изменение состояния покоя или движения тела происходит постепенно, а не мгновенно. При этом движение изменяется тем медленнее, чем больше инертность тела. Мерой инертности тела при поступательном движении является масса.
Первый закон Ньютона выполняется не во всякой системе отсчета. Системы, в которых он выполняется, называются инерциальными системами отсчета. Инерциальной системой отсчета является такая система, относительно которой свободная материальная точка, не подверженная воздействию других тел, движется равномерно и прямолинейно, или по инерции. Система отсчета, движущаяся по отношению к инерциальной системе отсчета с ускорением, является неинерциальной, и в ней не выполняются ни закон инерции, ни второй закон Ньютона, ни закон сохранения импульса.
Понятие «инерциальная система отсчета» является научной абстракцией. Реальная система отсчета всегда связывается с каким-нибудь конкретным телом (Землей, корпусом корабля и т.п.), по отношению к которому и изучается движение тех или иных объектов. Однако в природе нет неподвижных тел (тело, неподвижное относительно Земли, будет двигаться вместе с нею ускоренно по отношению к Солнцу и звездам), поэтому любая реальная система отсчета может рассматриваться как инерциальная лишь с той или иной степенью приближения. С очень высокой степенью точности инерциальной можно считать гелиоцентрическую (звездную) систему с началом координат в центре Солнца и с осями, направленными на три звезды. Для решения большинства технических задач инерциальной системой можно считать систему отсчета, жестко связанную с Землей (не учитывается вращение Земли вокруг собственной оси и вокруг Солнца).
Как уже отмечалось, масса – это физическая величина, определяющая инерционные свойства материи. Масса – это свойство самого тела и, в отличие от веса, не зависит от места ее измерения (вес Р тела в разных точках земного шара различен: он максимален на полюсах и минимален на экваторе).
За единицу массы принят килограмм массы, равный массе эталона, сделанного из сплава иридия и платины. Следует отметить, что масса тела считается постоянной величиной только в классической механике Ньютона. В современной физике установлено, что масса тела увеличивается с увеличением скорости его движения.
Для описания воздействий тел (материальных точек) друг на друга вводится понятие силы. Под действием сил тела либо изменяют скорость движения, т.е. приобретают ускорения (динамическое проявление сил), либо деформируются, т.е. изменяют свою форму и размеры (статическое проявление сил). Таким образом, сила - это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры. В каждый момент времени сила характеризуется числовым значением (модулем), направлением в пространстве и точкой приложения.
Второй закон Ньютона – основной закон динамики поступательного движения – отвечает на вопрос, как изменяется механическое движение материального объекта (точки, тела) под действием приложенных к нему сил.
Второй закон Ньютона формулируется следующим образом: ускорение, приобретаемое материальной точкой (телом), прямо пропорционально действующей силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела):
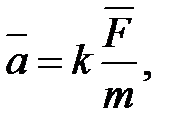 (2.3)
(2.3)
где 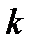 - коэффициент пропорциональности, зависящий от выбора системы единиц. В Международной системе (СИ)
- коэффициент пропорциональности, зависящий от выбора системы единиц. В Международной системе (СИ) 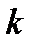 =1, поэтому
=1, поэтому 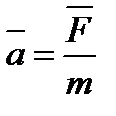 (2.4)
(2.4)
Второй закон Ньютона обычно записывается в следующей форме:
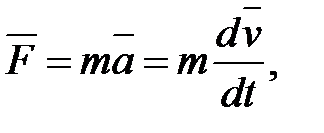 или
или 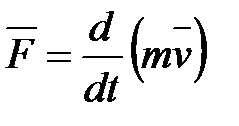 . (2.5)
. (2.5)
Вектор 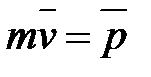 называется импульсом или количеством движения. В отличие от ускорения и скорости, импульс является характеристикой движущегося тела, отражающей не только кинематическую меру движения (скорость), но и его важнейшее динамическое свойство – массу.
называется импульсом или количеством движения. В отличие от ускорения и скорости, импульс является характеристикой движущегося тела, отражающей не только кинематическую меру движения (скорость), но и его важнейшее динамическое свойство – массу.
Таким образом, можно записать: 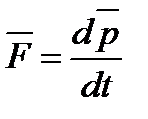 (2.6)
(2.6)
Выражение (2.6) является более общей формулировкой второго закона Ньютона: скорость изменения импульса материальной точки равна действующей на нее силе.
Это уравнение называется уравнением движения материальной точки.
Единица силы в системе СИ – ньютон (Н):
При действии на материальную точку нескольких сил справедлив принцип независимости действия сил: если на материальную точку действуют одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение, определяемое вторым законом Ньютона так, как если бы других сил не было:
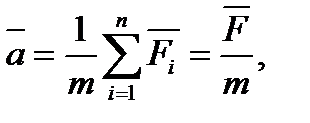
где сила 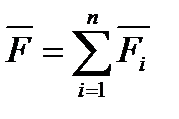 называется равнодействующей сил или результирующей силой.
называется равнодействующей сил или результирующей силой.
Второй закон Ньютона справедлив только в инерциальных системах отсчета. Первый закон Ньютона можно получить из второго закона: в случае равенства нулю равнодействующей силы ускорение также равно нулю, т.е. тело находится в покое или движется равномерно.
Воздействие тел (материальных точек) друг на друга всегда является взаимным и определяется третьим законом Ньютона (законом о равенстве действия и противодействия): действия двух тел друг на друга всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти тела:
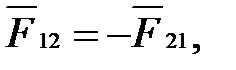 (2.7)
(2.7)
где 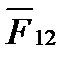 - сила, действующая на первое тело со стороны второго;
- сила, действующая на первое тело со стороны второго; 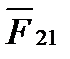 - сила, действующая на второе тело со стороны первого.
- сила, действующая на второе тело со стороны первого.
Необходимо помнить, что силы 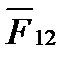 и
и 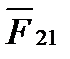 приложены к разным телам (материальным точкам) и поэтому не уравновешивают друг друга; они действуют парами и являются силами одной природы.
приложены к разным телам (материальным точкам) и поэтому не уравновешивают друг друга; они действуют парами и являются силами одной природы.
Из второго и третьего законов Ньютона вытекает закон сохранения импульса замкнутой системы.
Совокупность материальных точек (тел), рассматриваемых как единое целое, называется механической системой. Силы взаимодействия между материальными точками механической системы называются внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют внешние силы (они взаимно уравновешиваются), называется замкнутой или изолированной. В такой системе необходимо учитывать только силы взаимодействия между входящими в нее телами (внутренние силы). Строго говоря, изолированных механических систем в природе не существует.
Рассмотрим изолированную механическую систему, состоящую из n тел с массами m1, m2,…, mn. Обозначим скорости этих тел через 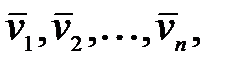 а внутреннюю силу, действующую на i-е тело со стороны k-го, - через
а внутреннюю силу, действующую на i-е тело со стороны k-го, - через 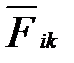 .
.
На основании второго закона Ньютона можно составить следующую систему уравнений движения всех тел системы:
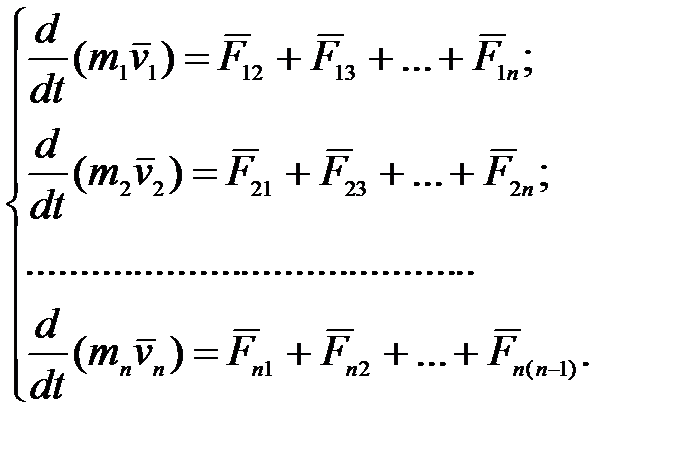
Складывая почленно эти уравнения и группируя силы 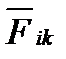 и
и 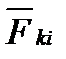 , получим:
, получим:
 .
.
Согласно третьему закону Ньютона 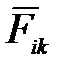 =-
=- 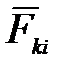 , поэтому все скобки в правой части этого уравнения равны нулю, т.е.
, поэтому все скобки в правой части этого уравнения равны нулю, т.е.
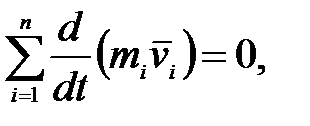 или
или 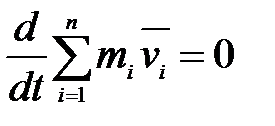 .
.
Векторная сумма 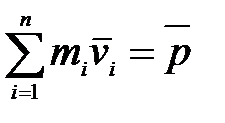 представляет собой импульс всей системы. Таким образом,
представляет собой импульс всей системы. Таким образом, 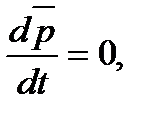 или
или 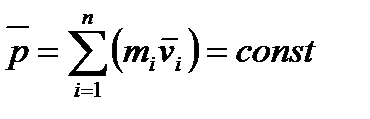 (2.9)
(2.9)
Выражение (2.9) представляет собой закон сохранения импульса: импульс замкнутой системы тел с течением времени не изменяется.
Закон сохранения импульса справедлив не только в классической механике; он выполняется и для замкнутых систем микрочастиц, т.е. действует и в квантовой механике. Другими словами, этот закон носит универсальный характер и является фундаментальным законом природы.
Закон сохранения импульса является следствием однородности пространства: при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства и законы движения не изменяются, т.е. не зависят от выбора положения начала координат инерциальной системы отсчета.
В классической механике из-за независимости массы от скорости импульс системы можно выразить через скорость ее центра масс. Скорость i-й материальной точки связана с ее радиусом-вектором 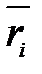 соотношением:
соотношением: 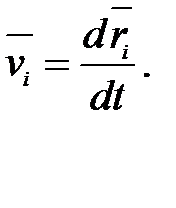
Следовательно, 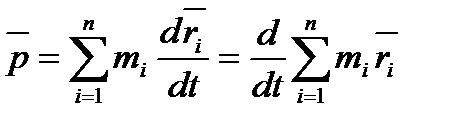 .
.
Центром масс или центром инерции системы материальных точек называется воображаемая тоска С, положение которой характеризует распределение массы этой системы. Ее радиус-вектор равен
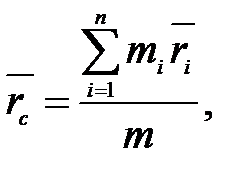 где
где 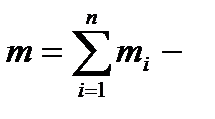 масса системы.
масса системы.
Скорость центра масс определяется выражением:
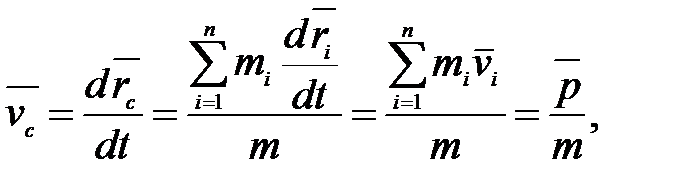
т.е. 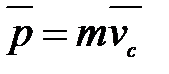 . (2.10)
. (2.10)
Другими словами, импульс системы равен произведению массы системы на скорость ее центра инерции. Подставив выражение (2.10) в (2.9), получим:
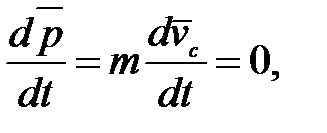
т.е. в изолированной механической системе центр масс находится в покое или движется равномерно и прямолинейно.
Если система незамкнутая (на нее действуют помимо внутренних и внешние силы), то выражение (2.9) с учетом (2.10) запишется следующим образом:
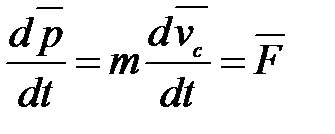 ,
,
или
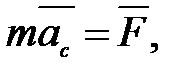 (2.11)
(2.11)
где 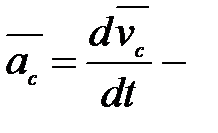 ускорение центра масс.
ускорение центра масс.
Из (2.11) вытекает закон (теорема) движения центра масс: центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, приложенных к системе.
Получим уравнение движения тела переменной массы (например, движение ракеты сопровождается уменьшением ее массы за счет истечения газов, образующихся от сгорания топлива).
Пусть в момент времени t масса ракеты m, а ее скорость 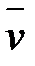 ; тогда по истечении времени dt ее масса уменьшится на dm и станет равной m–dm, а скорость увеличится до величины
; тогда по истечении времени dt ее масса уменьшится на dm и станет равной m–dm, а скорость увеличится до величины 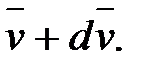 Изменение импульса системы за время dt будет равно:
Изменение импульса системы за время dt будет равно:
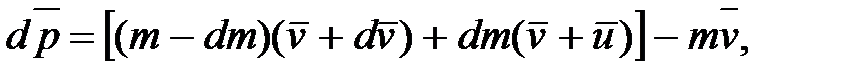
где 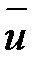 - скорость истечения газов относительно ракеты. Раскрывая скобки в этом выражении, получим:
- скорость истечения газов относительно ракеты. Раскрывая скобки в этом выражении, получим:
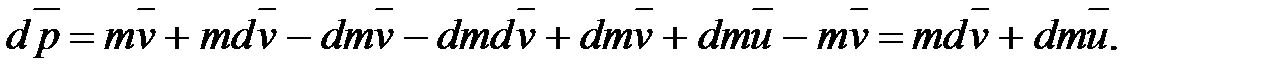
Если на систему действуют внешние силы, то 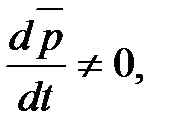 т.е.
т.е. 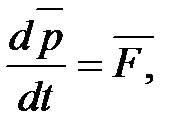 или
или  Тогда
Тогда 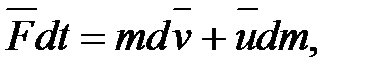 или
или 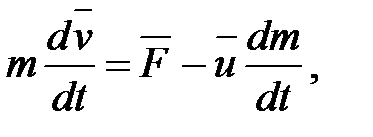 (2.12)
(2.12)
где член 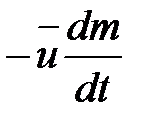 называют реактивной силой
называют реактивной силой 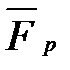 . Если вектор
. Если вектор 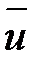 противоположен
противоположен 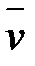 , то ракета ускоряется, а если совпадает с
, то ракета ускоряется, а если совпадает с 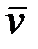 , то тормозится.
, то тормозится.
Таким образом, уравнение движения тела переменной массы имеет следующий вид:
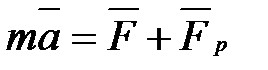 (2.13)
(2.13)
Уравнение (2.13) называется уравнением И.В. Мещерского.
Применим уравнение (2.12) к движению ракеты, на которую не действуют никакие внешние силы. Тогда, полагая 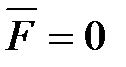 и считая, что ракета движется прямолинейно (скорость истечения газов постоянна), получим:
и считая, что ракета движется прямолинейно (скорость истечения газов постоянна), получим:
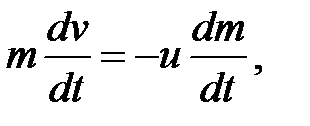
откуда
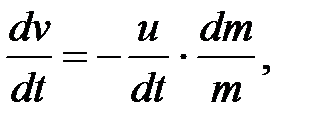
или
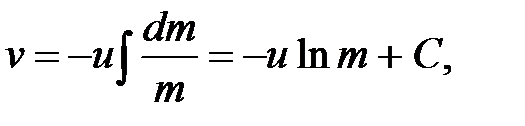
где С – постоянная интегрирования, определяемая из начальных условий. Если в начальный момент времени 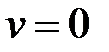 , а стартовая масса ракеты составляет m0, то
, а стартовая масса ракеты составляет m0, то 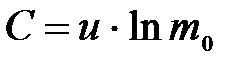 .Следовательно,
.Следовательно,
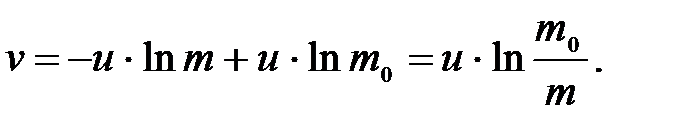 (2.14)
(2.14)
Полученное соотношение называют формулой К.Э. Циолковского. Из выражения (2.14) следуют следующие практические выводы:
а) чем больше конечная масса ракеты m, тем больше должна быть стартовая масса m0;
б) чем больше скорость истечения газов u, тем больше может быть конечная масса при данной стартовой массе ракеты.
Уравнения Мещерского и Циолковского справедливы для случаев, когда скорости 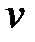 и
и 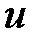 намного меньше скорости света с.
намного меньше скорости света с.
Тема 4. Работа и энергия
Единая мера различных форм движения материи называется энергией. Движение является неотъемлемым свойством материи. Поэтому всякое тело обладает энергией, являющейся мерой его движения. Для количественной характеристики качественно различных форм движения, изучаемых в физике, вводятся соответствующие им виды или формы энергии – механическая, внутренняя, электромагнитная и другие.
Причиной изменения состояния механического движения тела, а, следовательно, и его энергии, является взаимодействие тела с другими телами. Для характеристики воздействия этих тел на рассматриваемое тело в механике введено понятие силы. Поэтому можно говорить, что изменение движения и энергии вызывается силами. Процесс изменения энергии тела под действием силы называется процессом свершения работы, а приращение энергии тела в этом процессе называется работой, совершенной силой. Опыт показывает, что сила, приложенная к телу, совершает работу только тогда, если тело при этом перемещается.
| . |
| Fn |
| F |
| Fτ |
| v |
| α |
| Рис. 3.1 |
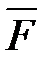 , тем больше, чем больше составляющая силы
, тем больше, чем больше составляющая силы 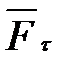 , касательная к траектории и чем больше путь s, пройденный телом за время действия силы:
, касательная к траектории и чем больше путь s, пройденный телом за время действия силы:
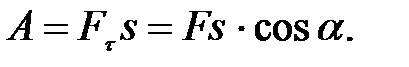 (3.1)
(3.1)
Если рассматривать достаточно малое перемещение, то движение материальной точки можно считать прямолинейным, а силу – постоянной. Поэтому элементарная работа, совершаемая силой 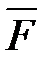 на перемещении
на перемещении  равна:
равна:
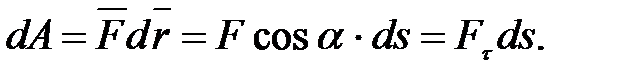 (3.1')
(3.1')
Работа, совершаемая силой 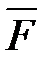 на конечном пути s (путь 1-2 на рис. 3.2), равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках:
на конечном пути s (путь 1-2 на рис. 3.2), равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках:
| Fs=f(s) |
| dA |
| A |
| ds |
| s |
| Fτ |
| Рис. 3.3 |
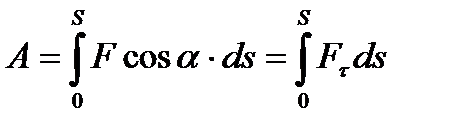 (3.2)
(3.2)
Очевидно, что работа, совершаемая силой 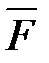 на пути 0-s, численно измеряется площадью, заштрихованной на рис. 3.3. Если сила
на пути 0-s, численно измеряется площадью, заштрихованной на рис. 3.3. Если сила 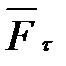 не зависит от s (
не зависит от s (  const), то
const), то 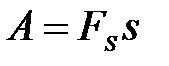 .
.
Единица работы – джоуль (Дж): 1 Дж – это работа, совершаемая силой в 1 Н на пути в 1 м:
1 Дж = 1 Н·м.
Если работа, совершаемая силой











