Глава 5. ХИМИЧЕСКАЯ ТЕРМОДИНАМИКА
После усвоения материала Главы 5 студент должен:
Знать
• основные понятия и определения химической термодинамики, функции состояния;
• закон Гесса и следствия из него;
• I, II и III законы термодинамики;
• критерии возможности протекания химической реакции;
Уметь
• рассчитывать изменение энтальпии химических реакций;
• давать прогноз изменения энтропии системы при стандартных условиях;
• вычислять теплоту гидратации;
• рассчитывать возможность самопроизвольного протекания реакции при стандартных условиях;
• рассчитывать температуру, выше которой реакция идет самопроизвольно;
• экспериментально определять тепловой эффект реакции нейтрализации;
Владеть
• теоретическими основами химической термодинамики;
• способом экспериментального определения теплового эффекта реакции нейтрализации;
• способами решения задач по химической термодинамике.
Основные понятия и определения
Химические реакции заключаются в разрыве одних и образовании других связей, поэтому их протекание сопровождается выделением или поглощением энергии в виде тепла, света, работы расширения газов. Раздел химии, изучающий тепловые эффекты реакций называется термохимией. В основе термохимии лежат термодинамические методы. Термодинамика – наука, изучающая закономерности превращения энергии из одной формы в другую. Объектом исследования термодинамики является система.
Система– тело или группа тел, находящихся во взаимодействии, и мысленно или с помощью поверхности выделенных из окружающей среды.
По характеру обмена с окружающей средой веществом и энергиейразличают: 1) изолированную – не обменивающуюся с окружающей средой веществом и энергией; 2) закрытую – обменивающуюся только энергией; 3) открытаую – обменивающуюся с окружающей средой веществом и энергией.
Система, внутри которой нет поверхности раздела, и одинаковая по свойствам во всех своих точках, называется гомогенной. Гетерогенной системой называется система внутри которой есть поверхность раздела, (металл – раствор электролита, лед – вода, вода – водяной пар).
Состояние системы определяется термодинамическими параметрами: экстенсивные параметры (пропорциональные количеству вещества) – объем, масса, плотность, концентрация, заряд, площадь поверхности; и интенсивные параметры (аналоги сил) – температура, давление, электрический потенциал, поверхностное натяжение. Параметры состояния связаны друг с другом функциональными зависимостями.
Переход системы из одного состояния в другое называется процессом. Процессы, протекающие при постоянных значениях температуры, объема, давления называются соответственно: изотермическими, изохорными, изобарными. Процессы, при которых система не обменивается теплотой с окружающей средой, а связана со средой только работой, называются адиабатными. Коме того, различают обратимый процесс, который допускает возможность возвращение системы в первоначальное состояние без затраты энергии и протекающий бесконечно медленно. Процессы не удовлетворяющие условиям обратимости – необратимые.
Различают равновесное и неравновесное состояние системы. Равновесным состоянием называется такое, в котором при отсутствии внешних воздействий параметры системы не изменяются во времени. В термодинамике не рассматривается ход процесса, а только его результат. Результатом же в классической термодинамике всегда является равновесное состояние системы и среды.
Функции состояния
Термодинамические свойствасистемы описываются функциями состояни, которые зависят от начального и конечного состояний системы и не зависят от пути процесса.
5.2.1. Внутренняя энергия (U)
Внутренняя энергия (U) включает в себя энергии всех видов движения и взаимодействия частиц системы (молекул, атомов, ядер, электронов, протонов, нейтронов и т.д.) кроме кинетической энергии движения самой системы и потенциальной энергии положения ее в поле тяготения.
Определить абсолютное значение внутренней энергии системы невозможно, но изменение энергии (DU) в процессе перехода системы из одного состояние в другое (в процессе химической реакции) можно измерить. Известны две формы передачи энергии: упорядоченная форма – работа, неупорядоченная – теплота. Внутренняя энергия системы может изменяться за счет обмена теплотой или совершения работы с окружающей средой.
Первый закон термодинамики: поглощаемая системой теплота(q) расходуется на увеличение внутренней энергии (DU) и совершение работы против внешних сил (DA):
| Dq = DU + DA. | (5.1) |
Первый закон термодинамики – одна форм из выражений закона сохранения энергии.
Запишем термохимическое, т.е. содержащее величину теплового эффекта реакции в кДж, уравнение реакции получения водорода:
Zn(к) + H2SO4(р-р) → ZnSO4(р-р) + H2(г) +165,7 кДж.
Указанный тепловой эффект реакции наблюдается в изохорных условиях, если реакция проводится при постоянном объеме, например, в запаянной ампуле (V = const). Тепловой эффект связан с понижением внутренней энергии системы. Изменение внутренней энергии системы равно изохорному тепловому эффекту реакции, взятому с обратным знаком: DU =–Qv. Если ту же реакцию проводить при изобарных условиях, тепловой эффект реакции будет иным.
5.2.2. Энтальпия (DН)
Для характеристики системы и тепловых эффектов реакций при постоянном давлении используют - энтальпию. Поскольку большинство реакций протекает именно при таких условиях, эту функцию чаще всего используют для их термодинамического описания.
Энтальпия(DН) – термодинамическая функция состояния, характеризующая изменение энергии системы при постоянном давлении.
Тепловой эффект реакции между цинком и кислотой в цилиндре с подвижным поршнем, который поднимается без трения при расширении выделяющегося водорода, т.е. при постоянном давлении (изобарные условия), составяет 162,2 кДж. Тепловой эффект изобарной реакции меньше, чем тепловой эффект изохорной реакции на величину работы по расширению против сил внешнего давления, что наблюдается для реакций с участием газов. Разница между DU иDH незначительна для реакций в жидкой или твердой фазе.
Работа против сил внешнего давления равна произведению давления (Р) на площадь поршня (S) и на высоту его подъема (∆h): A = P∙SΔh, и тогда Qp= Qv – pDV.
Из полученного соотношения следует, что энтальпия складывается из изменения внутренней энергии системы и работы против нешних сил:
| DН = DU + pDV | (5.2) |
DН, как функция состояния, зависит от параметров системы, поэтому, чтобы сравнивать тепловые эффекты реакций, их приводят к стандартным условиям: р = 101 кПа, t = 25°С (или Т = 298 K). Обозначают изменение энтальпии при стандартных условиях: DН°298. Энтальпии образования простых веществ приняты равными нулю.
Для оценки тепловых эффектов образования сложных веществ из простых, которые имеют несколько аллотропных модификаций, рассматривается реакция с формой вещества устойчивой при стандартных условиях, поскольку энтальпия образования неустойчивых модификаций не равна нулю.
Тепловой эффект образования 1 моль вещества из простых веществ, устойчивых при стандартных условиях, называетсястандартной энтальпией образования.
Значения энтальпий образования веществ – справочные величины. Обозначаются: DН°f,298 или DН°обр,298.
Тепловой эффект реакции при постоянном давлении равен изменению энтальпии: если DН < 0 – экзотермическая реакция (энергия в ходе реакции выделяется в окружающую среду), если DН > 0 – эндотермическая реакция энергия поглощается системой).
От агрегатных состояний реагирующих веществ и продуктов зависят тепловые эффекты реакций. Например, тепловой эффект реакции получения воды зависит от того, в котором агрегатного состояния она образуется, в виде жидкости или в виде паров:
H2(г) + 1/2O2(г) = H2O(ж); DНр = –285,85 кДж,
H2(г) + 1/2O2(г) = H2O(г); DНр = –241,84 кДж.
Разница тепловых эффектов реакций образования воды в жидком и газообразном состояниях составляет теплоту конденсации воды:
DНконденсации = –44,01 кДж/моль.
Чтобы указать тепловой эффект реакции, относящийся к одному молю образующегося вещества, в данном термохимическом уравнении использованы дробные коэффициенты.
Закон Гесса
Тепловой эффект получения жидкой воды равен +285,85 кДж/моль, не зависимо от пути процесса и числа последовательных стадий. Воду можно получить сразу жидкой, а можно получитьее в виде паров, а потом сконденсировать, т.е. в две стадии, что и показано на графике (рис. 5.1). Проведенный расчет является подтверждением основного закона термохимии, открытого отечественным химикрм Г.И. Гессом в 1841 г.: Изменение энтальпии зависит только от вида и состояния исходных веществ и продуктов реакции и не зависит от пути перехода.
С помощью закона Гесса можно рассчитать тепловой эффект практически любой реакции, используя энтальпии образовния исходных веществ и продуктов реакции.
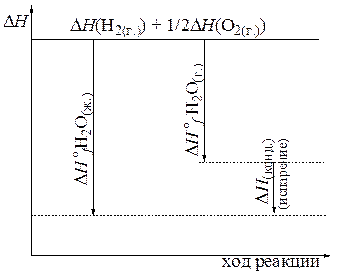
Рис. 5.1. Изменение энтальпии в зависимости от агрегатного состояния конечных продуктов
Рассмотрим некоторые следствия из закона Гесса:
1) Энтальпия разложения химического соединения равна энтальпии его образования из тех же продуктов, в том же состоянии, взятой с противоположным знаком:
| DН°обр,298 = –DН°разл,298 | (5.3) |
Чтобы разложить жидкую воду на кислород и водород, потребуется затратить энергию равную 285,85 кДж/моль.
2) Разность энтальпий реакций образования разных продуктов от одинаковых исходных веществ равна энтальпии перехода одного продукта в другой (см. рис. 5.1). Так разность энтальпий образования из кислорода и водорода пара и жидкой воды равна теплоте конденсации водяного пара в жидкость и составляет –44,01 кДж/моль.
3) Разность энтальпий реакций, приводящих к одному продукту от разных начальных веществ, равна энтальпии перехода одного исходного вещества в другое. Т.е. чтобы разложить жидкую воду надо затратить 44,01 кДж/моль энергии, чтобы перевести ее сначала в пар.
4) Энтальпия реакции равна разности сумм энтальпий образования продуктов и энтальпий образования исходных веществ с учетом стехиометрических коэффициентов в уравнении реакции:
| DНр= SDН°f,298 прод – SDН°f,298 исх. в-в | (5.4) |
Пользуясь следствиями из закона Гесса можно c учетом коэффициентов в уравнении реакции рассчитать энтальпии реакций и определить возможность их протекания. А также рассчитать энтальпии образования веществ, которые еще не получены или которые нельзя получить непосредственно из простых веществ.
5.2.4. Энтропия (S)
Самопроизвольное протекание некоторых процессов не сопровождается энергетическими эффектами. Например, газ расширяясь в пустоту, при хаотичном движении его молекул занимает весь предоставленный объем, но до меньшего объема спонтанно он не сжимается. Спонтанно тело не станет горячее окружающей среды, а будучи нагретым самопроизвольно отдаст ей тепло. Т.е. существует нечто, определяющее направление самопроизвольного изменения.
Если два различных инертных газа поместить в контейнер, разделив перегородкой, то убрав перегородку между двумя частями контейнера, получим смесь газов которая займет весь предоставленный объем. Вероятность возвращения газов в исходное состояние ничтожно мала. Т. е. система переходит, в более вероятное (менее упорядоченное) состояние равновесия, в котором она может пребывать неограниченно долго благодаря хаотичному движению молекул.
Из повседневного опыта следует, что направлением самопроизвольных изменений управляет рассеивание. Функция, которая показывает, как изменяется рассеивание энергии при переходе системы из одного состояния в другое выведена статистичеки с использованием теории вероятности.
Состояние системы есть совокупность микросостояний частиц, ее составляющих (т.е. мгновенных скоростей разных видов движений и координат частиц). Число микросостояний системы называется термодинамической вероятностью (W). Если системы объединяются в одну, то их вероятности, в отличие от энергий не складываются, а перемножаются: W = W1·W2.
Поскольку любая, даже самая простая система, например, 1 моль газа содердит 6,02·1023 молекул, и характеризуется соответствующим огромным числом микросостояний и значением термодинамической вероятности, становится ясно, что необходимо представить вероятность в виде функции, которая бы принимала небольшие значения и при объединении систем ее значения суммировались. Такой функцией является логарифм: ln(ab) = lna + lnb.
Для оценки энергетических эффектов необходимо, чтобы эта функция имела размерность энергии. Введя в уравнение универсальную газовую постоянную (работа расширения 1 моля газа при нагревании его на 1 градус), имеющую размерность Дж/моль×K получили энтропию (5.5):
| S = R·lnW,(Дж/моль×K) | (5.5) |
Энтропия(S) – функция термодинамического состояния, являющаяся мерой неупорядоченности системы.
Энтропия вещества в стандартном состоянии называется стандартной энтропией (S°298 – справочная величина).
Функция состояния, введенная Клаузисом и названная им энтропией, рассматривалась как приведенная теплота: 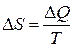 .
.
Позднее Больцман, анализируя энтропию на молекулярном уровне, связав с хаосом, интерпретировал ее как меру неупорядоченности системы. Математически доказывается идентичность термодинамической и статистической энтропии.
Энтопия как мера неупорядоченности системы зависит от температуры, что следует из третьего начала термодинамики.
Третье начало термодинамики: при абсолютном нуле энтропия всех тел равна нулю.
При абсолютном нуле частицы материи неподвижны, система находится в упорядоченном состоянии. По мере повышения температуры растет скорость движения частиц, возрастает число их микросостояний, термодинамическая вероятность и энтропия вещества. Исходя из нулевого значения, можно определить не только приращение энтропии, но и абсолютное значение.Абсолютную энтропию химических веществ вычисляют с помощью статистической термодинамики.
Резкое возрастание энтропии (неупорядоченности) вещества имеет место при переходе из жидкого в газообразное состояние вещества. Увеличение количества вещества, объемов газов, увеличение числа атомов в молекуле, порядкового номера элемента, все это также ведет к возрастанию энтропии. Для изолированной системы можно сделать вывод о возможности протекания реакции на основании изменения энтропии системы, в соответствии со вторым законом термодинамики.
Второй закон термодинамики: в изолированных системах самопроизвольно идут только такие процессы, которые сопровождаются возрастанием энтропии: DS > 0.
Не прибегая к сложным расчетам, можно сказать, что энтропия в ходе реакции: 2NО(г) + О2(г) = 2NО2(г) уменьшается (DS < 0), т.к. исходные газообразные вещества занимают 3 объема, а продукты – 2. Но эта реакция, идет самопроизвольно, т.к. сопровождается выделением тепла и понижением энтальпии системы.
Итак, химические процессы имеют две движущие силы: 1) понижение энергии системы, что можно рассматривать как повышение энтропии окружающей среды, куда выделяется теплота, 2) возрастание энтропии системы.
Первая тенденция количественно характеризуется для изобарно-изотермических условий изменением энтальпии DНр (кДж/моль), вторая – изменением энтропийного фактора – ТDS (Дж/моль). Объединяет энтальпийный и энтропийный факторы энергия Гиббса(DG) (или изобарно-изотермический потенциал).
5.2.5. Энергия Гиббса (DG)
Энергия Гиббса(DG) (или изобарно-изотермический потенциал) – критерий самопроизвольного протекания реакции при изобарно-изотермических условиях:
| DG = DН – ТDS, кДж | (5.6) |
Изменение энергии Гиббса при образовании 1 моль вещества из простых веществ, устойчивых при стандартных условиях называется стандартной энергией Гиббса образования вещества (DG°f,298 –справочная величина).
Изменение энергии Гиббса в химической реакции можно рассчитать в соответствии с законом Гесса как разность сумм энергии Гиббса продуктов и исходных веществ с учетом их стехиометрических коэффициентов:
| DGр = SDG°f,298 прод – SDG°f,298 исх. в-в | (5.7) |
Для самопроизвольных реакций DGр<0. Отрицательные значение энергии Гиббса имеет место, если реакция экзотермическая (DНр < 0) и сопровождается повышением энтропии системы (DSр > 0). Если DНр > 0, и DSр > 0, или DНр < 0 и DSр < 0, величина потенциала Гиббса может быть как меньше, так и больше 0, что зависит от соотношения величин энтальпии реакции и энтропийного фактора. Так при высоких температурах увеличение энтропийного (ТDSр) фактора может оказаться больше энтальпийной составляющей, и реакция, невозможная при стандартных условиях, станет возможной при повышенной температуре. Если же DНр > 0, а DSр < 0, то при любых температурах DGр > 0, и возможна только обратная реакция.
В состоянии равновесия DGр = 0, тогда DНр = ТDSр, откуда:
 , ,
| (5.8) |
где Т – температура равновесия между прямой и обратной реакцией.
Выражение (5.6) можно записать в виде:
| DНр = DGр + ТDSр. | (5.9) |
Из уравнения видно, что энергия системы может быть израсходована на увеличение энтропии за счет рассеивания тепла в окружающую среду, это связанная энергия (ТDSр). DGр – свободная энергия, часть энергии, которую можно превратить в работу:
| –DG= Ap. | (5.10) |
где Ap – работа системы при p = const.
Реакция совершается самопроизвольно только тогда, когда работа положительна. Пределом течения реакции является состояние равновесия, соответствующее условию: Ap = 0. Равновесное – наиболее вероятное состояние системы, состояние наибольшего беспорядка с максимальной энтропией.
Контрольные вопросы
1. Дайте определение термодинамической системы и ее параметров.
2. Дайте определение внутренней энергии системы как функции состояния.
3. Приведите формулировку первого закона термодинамики.
4. Объясните различие величин тепловых эффектов реакций, проведенных при постоянном объеме и постоянном давлении.
5. Дайте определение энтальпии как функции состояния и стандартной энтальпии образования вещества.
6. Приведите формулировку закона Гесса и следствий из этого закона.
7. Охарактеризуйте энтропию как функцию состояния, являющуюся мерой неупорядоченности системы.
8. Приведите формулировку второго и третьего законов термодинамики.
9. Охарактеризуйте энергию Гиббса, как критерий возможности протекания химической реакции.
10. Объясните влияние температуры на направление протекания химической реакции. Как рассчитать температуру, выше которой реакция идет самопроизвольно?
Примеры решения задач
Пример 1. Рассчитайте энтальпию реакции окисления оксида углерода (II) при стандартных условиях. Укажите, экзо- или эндотермической является данная реакция.
| Дано (из табл. 3): | Решение: | |
| В-ва | DHof,298, кДж/моль | 2СO(г) + O2(г)= 2СO2(г) |
| CO(г) | -110,5 | DH°298 реакц =SDH°298 прод – SDH°298 исходн |
| O2 | С учетом коэффициентов: | |
| CO2(г) | –393,5 | DH°298 реакции= 2 (–393,5) – [2(–110,5) + 1(0)]= –566 (кДж) |
| Найти: DH°298 реакции | Ответ: DH°298 реакции = –566 кДж, реакция экзотермическая, т.к. DH°298 < 0. |
Пример 2. При сгорании 3,2 г серы выделилось 29,7 кДж. Рассчитайте теплоту образования оксида серы (IV).
| Дано: | Решение: 3,2 г 29,7 кДж |
| mсеры = 3,2 г | S(к)+ O2(г) = SO2(г) + Q; Q = –DHр |
| Q = –29,7 кДж | 1 моль 1 моль х кДж |
| Найти:DHof,298 (SO2) | M(S) =32 г/моль |
Составим пропорцию:  3,2 : 32 = 29,7 : х; х = 297 (кДж).
Так как рассчитанный тепловой эффект реакции относится к образованию 1 моль SO2 из простых веществ в их устойчивых состояниях при стандартных условиях, то DH°f,298(SO2) = –297 кДж/моль. 3,2 : 32 = 29,7 : х; х = 297 (кДж).
Так как рассчитанный тепловой эффект реакции относится к образованию 1 моль SO2 из простых веществ в их устойчивых состояниях при стандартных условиях, то DH°f,298(SO2) = –297 кДж/моль.
|
Ответ: DH°f, 298(SO2) = –297 кДж/моль
Пример 3. Не производя расчетов, предскажите знак изменения энтропии системы при стандартных условиях для следующих процессов:
1) 2H2O(г) = O2(г) + 2H2(г); 2) NH3(г) + HCl(г) = NH4Cl(к);
3)Ba2+(р) + SO42–(р) = BaSO4(к)
Решение. Прогноз без расчета DSреакции возможен в тех случаях, когда меняется объем системы. Так с уменьшением объема газообразных веществ или образованием кристаллических продуктов из газообразных или жидких веществ степень беспорядка уменьшается (DS < 0).
1) В реакцию вступают два объема газа, а образуется 3 объема. В результате объем системы увеличивается, и степень беспорядка возрастает, DS > 0.
2) Объем твердого продукта меньше объема исходных газов, т.е. упорядоченность системы возрастает, DS < 0.
3) Ионы Ba2+ и SO42– из раствора перешли в кристаллическое вещество, DS < 0.
Пример 4. Энтальпия образования СО2 из графита равна -393,5 кДж/моль, а из алмаза равна –395,4 кДж/моль. Вычислите энтальпию перехода графита в алмаз.
| Дано: | Решение: |
| DH°f, 298(СO2)1 =-393,5 кДж/моль | Воспользуемся третьим следствием из закона Гесса: |
| DH°f, 298(СO2)2 = –395,4 кДж/моль | DH°3 = DH°f, 298(СО2)1 - DH°f, 298(СО2)2 DH°3 =-393,5 – (-395,4) = 1,9 (кДж/моль) |
| Найти: DH°3 (перехода графита в алмаз) | Ответ: энтальпия перехода графита в алмаз равна 1,9 кДж/моль. |
Пример 5. Рассчитайте, возможно ли, протекание реакции восстановления оксида железа (II) водородом при температуре 25°С. Найдите температуру, выше которой указанная реакция может протекать самопроизвольно.
| Дано: t1 = 25°C, Т1 = 298 K (стандартные условия), Из таблицы приложения № 3: | |||
| Вещество | DH°f,298 кДж/моль | DS°298 кДж/моль×К | DG°f,298 кДж/моль |
| FeO(т) | –264,8 | 0,061 | –244,3 |
| H2O(ж) | –241,8 | 0,190 | –228,6 |
| H2(г) | 0,130 | ||
| Fe(к) | 0,027 | ||
| Найти: Т2(равновесия). |
Решение:
FeO(к)+ H2(г)= Fe(к)+ H2O(г)
DG°298 р= SDG°f298(прод) – SDG°f298 (исх.в-в)
DG°298 р = –228,6 – (–244,3) = 15,7 (кДж)
Из уравнения DG = DH – TDS найдем Травн
При равновесии: DG = 0, DH = TDS, T = DH/DS
DH°298 р= –241,8 – (–264,8) = 23 (кДж)
DS°298р = 0,19 + 0,027 – 0,061 – 0,13 = 0,026 (кДж/К)
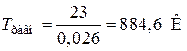 .
.
Ответ: при Т = 298 К данная реакция невозможна т.к. DG°298 р > 0. Самопроизвольное протекание прямого процесса возможно при Т > 884,6К.
Задачи для самостоятельного решения
Вариант 1
1. Рассчитайте стандартную энтальпию реакции 2NO + 3O2 = 2NO2. Укажите, экзо- или эндотермической является данная реакция.
2. Рассчитайте количество энергии, выделяющейся при сжигании 300 г этилового спирта, если тепловой эффект реакции С2Н5ОН(ж)+3О2(г)=2СО2(г)+3Н2О(г) составляет 1235 кДж
3. Предскажите, производя расчетов, знак изменения энтропии при стандартных условиях для процесса: CaO(к) + CO2(г) ® CaCO3(к).
4. Рассчитайте значение потенщиала Гиббса для реакции CO(г) + O2(г) ® CO2(г) и сделайте вывод о возможности протекания процесса при стандартных условиях, предварительно расставив коэффициенты. Найдите температуру равновесия этой реакции.
5. Рассчитайте стандартную энтропию нитрата меди, если стандартная энтропия реакции 2CuO(к) + 4NO2(г) + O2(г) = 2Cu(NO3)2(к) составляет 867 Дж/К.
Вариант 2
1. Рассчитайте стандартную энтальпию реакции: Fe(к) + O2(г) → Fe2O3(к). Расставьте коэффициенты. Укажите экзо- или эндотермической является данная реакция.
2. Сколько угля надо сжечь, чтобы получить 7000 кДж энергии?
3. Предскажите, не производя расчетов, знак изменения энтропии при стандартных условиях для процесса: AsF5(г) ® AsF3(г) + F2(г).
4. Рассчитайте DG° реакции СаСО3(к) ® СаО(к) + СО2(г) для температуры 1500°С.
5. По термохимическому уравнению реакции сгорания сероводорода: H2S(г) + 1,5O2(г) = H2O(г) + SO2(г); DH°р= –518,4 кДж/моль вычислите стандартную энтальпию сероводорода.
Вариант 3
1. Рассчитайте стандартную энтальпию реакции: Cr2O3(к) + 2Al(к) = 2Cr(к) + Al2O3(к). Укажите, экзо- или эндотермическим является данный процесс.
2. Определите теплоту сгорания 1 м3 (н.у.) ацетилена, если тепловой эффект реакции 2С2Н2(г) + 5О2(г) = 4СО2(г) + 2Н2О(г) составляет 2600 кДж.
3. Не производя расчетов, предскажите знак изменения энтропии при стандартных условиях для процесса: CS2(ж) + O2(г) ® CO2(г) + SO2(г).
4. Определите, может ли быть восстановлена медь по реакции CuO(к) + H2(г) = Cu(к) + H2O(г) при 500 К.
5. Рассчитайте стандартную энтропию реакции, выражающуюся схемой: SO2(г) + H2S(г) → S(к) + H2O(ж).
Вариант 4
1. Рассчитайте стандартную энтальпию реакции СаО(к) + СО2(г) = СаСО3(к). Укажите, экзо- или эндотермической будет эта реакция.
2. Вычислите теплоту растворения кристаллогидрата Na2SO3·7H2O, если теплота растворения сульфита натрия (Na2SO3) равна 11,3 кДж/моль, теплота гидратации этой соли (Na2SO3 ®Na2SO3·7H2O ) составляет 58,16 кДж/моль.
3. Предскажите, не производя расчетов, знак изменения энтропии при стандартных условиях для процесса, протекающего по схеме: HF(г) + N2(г) ® NF3(г) + H2( г).
4. Возможно ли протекание реакции C(к) + Fe2O3(к) ® Fe(к) + CO(г) при температуре 1300оC?
5. Рассчитайте изменение энтропии при стандартных условиях для реакции: C2H2(г) + O2(г) → CO2(г) + H2O(г).
Вариант 5
1. Рассчитайте стандартную энтальпию реакции NiO(к) + Al(к) → Ni(к) + Al2O3(к). Расставьте коэффициенты. Укажите, экзо- или эндотермической является данная реакция.
2. Рассчитайте теплоту гидратации безводного сульфата меди (CuSO4 → CuSO4·5H2O), если при растворении одного моля безводного сульфата меди выделяется 66,5 кДж, а при растворении 1 моля кристаллогидрата поглощается 11,7 кДж.
3. Расставьте коэффициенты и, не производя расчетов, предскажите знак изменения энтропии при стандартных условиях для процесса: Fe2O3(к) + H2(г) ® FeO(к) + H2O(г).
4. Возможно ли самопроизвольное протекание при стандартных условиях реакции H2S(г) + O2(г) ® H2O(г) + SO2(г). Рассчитайте температуру, выше которой реакция протекает самопроизвольно.
5. Значение стандартной энтропии реакции 4Na2SO3(к) = 3Na2SO4(к) + Na2S(к) равно –60 Дж/К. Рассчитайте стандартную энтропию сульфита натрия.
Вариант 6
1. Укажите, экзо или эндотермической является реакция Fe3O4(к) + CO(г) ® FeO(к) + CO2(г). Рассчитайте, предварительно расставив коэффициенты, изменение энтальпии при стандартных условиях для этой реакции.
2. Вычислите теплоту образования формальдегида, горение которого протекает согласно уравнению НСОН(г) + О2(г) = СО2(г) + Н2О(ж); DH°р = –560 кДж.
3. Предскажите, не производя расчетов, знак изменения энтропии при стандартных условиях для процесса NO(г)+O2(г)®NO2(г).
4. Определите, может ли может ли протекать реакция 3MgO(к) + 2Cr(к) = 3Mg(к) + Cr2O3(к) при 298 К, 1000 К.
5. Значение стандартной энтропии реакции 2H2O(ж) + 2SO2(г) + O2(г) = 2H2SO4(ж) составляет –527 Дж/К. Рассчитайте стандартную энтропию серной кислоты.
Вариант 7
1. Рассчитайте изменение энтальпии при стандартных условиях для реакции Са(ОН)2(к) = СаО(к) + Н2О(ж). Укажите, экзо или эндотермической является эта реакция.
2. Пользуясь термохимическим уравнением, 2NH3(г) + H2O(г) + SO3(г) = (NH4)2SO4(к); DH°р = –451 кДж, рассчитайте стандартную энтальпию образования сульфата аммония
3. Предскажите, не производя расчетов, знак изменения энтропии при стандартных условиях для процесса (предварительно расставьте коэффициенты в схеме реакций): KMnO4(к) ® K2MnO4(к) + MnO2(к) + O2(г).
4. Возможно ли самопроизвольное протекание реакции SO2(г) + NO2(г) = SO3(г) + NO(г) при стандартных условиях и температуре 800 К.
5. Горение формальдегида НСОН протекает согласно уравнению НСОН(г) + О2(г) = СО2(г) + Н2О(ж); DH°р = –560 кДж. Сколько кДж энергии выделится при сгорании 500 г формальдегида?
Вариант 8
1. Укажите, экзо- или эндотермическим является процесс, протекающей по схеме: СаО(к) + Р2О5(к) ® Са3(РО4)2(к). Рассчитайте стандартную энтальпию этой реакции.
2. Не производя расчетов, предскажите знак изменения энтропии при стандартных условиях для процесса: C2H2(г) + О2 ® CO2(г) +H2O(г).
3. Рассчитайте тепловой эффект сжигания 4,8 кг серы, если тепловой эффект реакции S(к) + O2(г) = SO2(г) равен 297 кДж.
4. Рассчитайте стандартную энергию Гиббса для реакции FeO(к) + CO(г) = Fe(к) + CO2(г), определите температуру, при которой равновероятно протекание прямого и обратного процессов.
5. Вычислите стандартную энергию Гиббса образования оксида железа (III) по следующим данным: 1) 2Fe(к) + O2(г) = 2FeO(к); DG°298(I) = –490 кДж; 2) 4FeO(к) + O2(г) = 2Fe2O3(к); DG°298(II) = –504 кДж.
Вариант 9
1. Рассчитайте, расставив коэффициенты, стандартную энтальпию реакции Fe3O4(к) + H2(г) ® FeO(к) + H2O(г). Укажите, экзо- или эндотермической она является.
2. Рассчитайте тепловой эффект получения 1 кг карбида кальция по реакции СаО(к) + 3С(т) = СаС2(к) + СО(г) при стандартных условиях.
3. Не производя расчетов, предскажите знак изменения энтропии при стандартных условиях для процесса: BaO(к)+CO2(г)=BaCO3(к).
4. Вычислите, расставив коэффициенты, стандартную энергию Гиббса для реакции Cr2O3(к) + H2(г) ® Cr(к) + H2O(г). Определите температуру, выше которой процесс идет самопроизвольно.
5. Рассчитайте стандартную энтропию нитрата свинца, если значение стандартной энтропии реакции 2PbO(к) + 4NO2(г) + O2(г) = 2Pb(NO3)2(к) составляет –871 Дж/К.
Вариант 10
1. Укажите, экзо- или эндотермическим является процесс, протеекающий по схеме Fe2O3(к) + Mg(к) ® Fe(к) + MgO(к). Рассчитайте, значение стандартной энтальпии реакции
2. Определите тепловой эффект окисления 200 л аммиака по реакции 4NH3(г) + 5O2(г) = 4NO(г) + 6H2O(г) при стандартных условиях.
3. Не производя расчетов, предскажите знак изменения энтропии при стандартных условиях для процесса: C2H4(г) + H2(г) ® C2H6(г).
4. Определите, можно ли восстановить цинк по реакции ZnO(к) + Mg(к) ® Zn(к) + MgO(к) при 1500 К.
5. Рассчитайте стандартную энтропию хромата аммония, если для реакции 2(NH4)2CrO4(к) = Cr2O3(к) + N2(г) + 5H2O(ж) + 2NH3(г) значение стандартной энтропии реакции равно +661 Дж/К.
Вариант 11
1. Расставьте коэффициенты в уранении: H2S(г) + O2(г) ® S(к) + H2O(ж). Рассчитайте стандартную энтальпию реакции. Укажите, экзо- или эндотермической будет эта реакция.
2. Вычислите тепловой эффект превращения графит ® аморфный уголь на основании термохимических данных: С(графит) + О2(г) = СО2(г); DНр = –393,51 кДж, С(аморфный уголь) + О2(г) ® СО2(г); DНр = –409,20 кДж,.
3. Не производя расчетов, предскажите знак изменения энтропии при стандартных условиях для процесса: CH4(г) + O2(г) ® CO2(г) + H2O(г).
4. Рассчитайте стандартную энергию Гиббса для реакции CaCO3(к) = CaO(к) + CO2(г). Возможно ли протекание реакции при 1800 К?
5. Значение стандартной энтропии реакции 4KClO4(к) = 2KClO3(к) + 2KCl(к) + 5O2(г) равно 871 Дж/К. Рассчитайте стандартную энтропию KClO4.
Вариант 12
1. Для реакции PH3(г) + O2(г) ® P2O5(к) + H2O(ж) вычислите, расставив коэффициенты, стандартную энтальпию и укажите экзо- или эндотермической является эта реакция
2. По термохимическому уравнению: NH3(г) + HCl(г) = NH4Cl(к); –175 кДж рассчитайте стандартную энтальпию образования хлорида аммония.
3. Предскажите, не производя расчетов, знак изменения энтропии при стандартных условиях для процесса: H2(г)+O2(г) ®H2O(г), предварительно расставив коэффициенты.
4. Рассчитайте, возможно ли самопроизвольное протекание реакции PbS(к) + O2(г) ® PbO(к) + SO2(г) при 1200 К.
5. Рассчитайте стандартную энергию Гиббса образования оксида мышьяка (V) из простых веществ по следующим данным:
(I) 4As(к) + 3O2(г) = 2As2O3(к); DG
Дата добавления: 2017-11-21; просмотров: 4743;











