Молекулярная адсорбция

Речь идет об адсорбции из растворов неэлектролитов или слабых электролитов. Эти вещества адсорбируются в виде молекул. Особенность такой адсорбции в том, что поверхность адсорбента заполнена молекулами растворителя или адсорбата. Растворенное вещество может адсорбироваться, только вытесняя из поверхностного слоя молекулы растворителя, при этом происходит обменная адсорбция.

(2.4.6.1.1.) Модель идеального двумерного раствора адсорбата и растворителя (этот материал не даю)

Существует ряд моделей адсорбции молекул из разбавленных растворов.

Первая модель предполагает, что адсорбция сводится в образованию монослоя, прилегающего к поверхности адсорбента. Остальные слои — обычный раствор. Этот случай напоминает хемосорбцию газов, но с небольшой теплотой адсорбции и приводит к описанию адсорбции уравнением Ленгмюра

(Г=Г_∞ вс /1+ вс) или Фрейндлиха.

Вторая модель рассматривает адсорбцию как полимолекулярный слой, находящийся в монотонно спадающем потенциальном поле твердого адсорбента — уравнение БЭТ.

Модель идеального двумерного раствора адсорбата и растворителя предполагает:

1. поверхность однородна

2. площадь, занимаемая молекулой адсорбата равна площади, занимаемой молекулой растворителя

3. взаимодействие между всеми молекулами одинаковы

4. адсорбция мономолекулярна

Рассмотрим обмен между молекулами как квазихимическую реакцию: 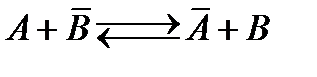с константой обмена.

Константа адсорбционного равновесия этой реакции (константа обмена) равна:

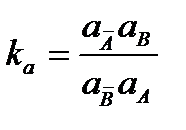(2.108)

В разбавленных растворах можно считать N_A=const

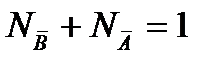
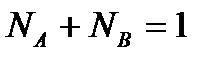(2.109)

коэффициент активности равен произведению концентрации на коэффициент активности a=Nγ, , поэтому константа k_а=k k_γ. (k — концентрационная константа). Константу коэффициентов активности в разбавленном растворе можно считать равной единице: k_γ=1, тогда:

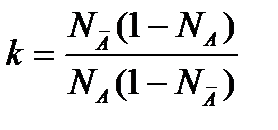(2.110)

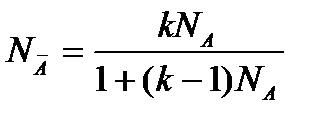— (2.111)

общее уравнение изотермы адсорбции из бинарных растворов с константой обмена,

Анализ уравнения показывает, что при N_A →0 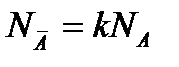. Рассмотрим графики изотерм адсорбции компонента:

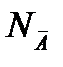
`````1

1 N<sub>A</sub>

Рис. 2.35. Изотермы адсорбции растворенного компонента в растворе

Кривая 1 отвечает условию k >> 1 и полученное уравнение приобретает вид уравнения (при малых концентрациях растворенного компонента):

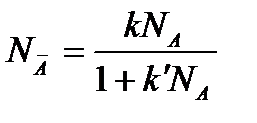
т.е. рассмотренная модель приводит к уравнению вида уравнения Ленгмюра: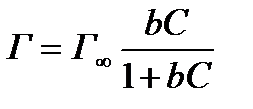

При k<<1 (кривая 2) получаем уравнение вида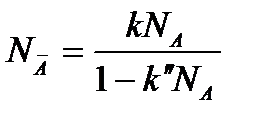

Если k≈1, т.е. величины сродства компонентов к адсорбенту близки, то на форму изотермы влияет коэффициент k<sub>γ</sub>.

Если поверхностный слой не идеален, то надо учитывать k<sub>γ</sub> адсорбата и растворителя. Если поверхность неоднородна, используют уравнения Темкина и Фрейндлиха.