Представление синусоидальных ЭДС, напряжений и токов комплексными числами

Комплексный метод при различных операциях с электрическими величинами позволяет учитывать как их абсолютные значения – модули, так и их фазы – аргументы. Метод основан на представлении векторов токов, напряжений и др. в комплексной плоскости и записи их комплексными числами. Комплексная плоскость представляет собой прямоугольную систему координат, где ось абсцисс является вещественной или действительной и обозначается +1. Ось ординат – мнимая ось, обозначается +j, где 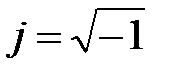. По вещественной оси откладывают действительную часть комплексного числа x, по мнимой – мнимую – jy(рис. 3.5). Комплексное число обозначают точкой.

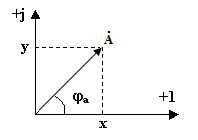
Рис.3.5

где:

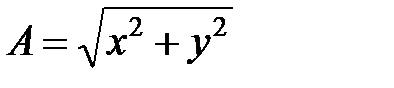- модуль числа;

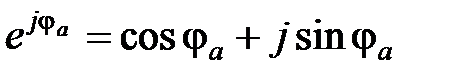- формула Эйлера;

е – основание натурального логарифма

Комплексное число имеет три формы записи: показательную, тригонометрическую и алгебраическую (3.5).

За положительное направление вращения вектора на комплексной плоскости принимают направление вращения против часовой стрелки относительно действительной оси.

Пусть нам задано ЭДС, напряжение и ток в синусоидальной форме.

Перейдём к комплексной форме:

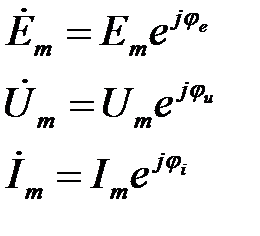
Аналогично для действующих значений этих величин:

На практике символический (комплексный) метод расчёта цепей синусоидального тока получил широкое распространение. Метод называется символическим потому, что токи и напряжения заменяются их комплексными изображениями или символами.

Его сущность состоит в том, что при синусоидальном токе можно перейти от дифференциальных уравнений мгновенных значений электрических величин к алгебраическим уравнениям составленных относительно комплексов тока и ЭДС. При этом, в любом уравнении составленном по закону Кирхгофа мгновенное значение тока i заменяют комплексной амплитудой ток 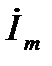, мгновенное значение напряжения u соответствующим комплексом .

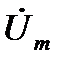Законы Кирхгофа формулируются:

1. Сумма комплексных токов в узле электрической цепи равна нулю: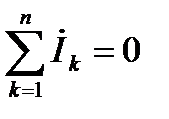

2. Сумма комплексных ЭДС в контуре равна сумме комплексных падений напряжений в этом контуре: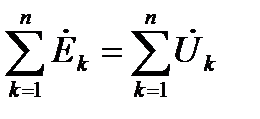

Как показано выше мгновенное значение напряжения на активном сопротивлении R 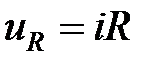заменяется комплексом 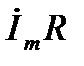, по фазе совпадающим с током 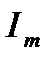. Мгновенное значение напряжения на индуктивности 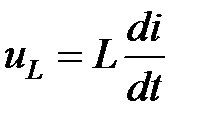- заменяется комплексом 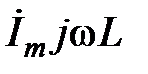, опережающим ток 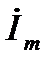на 90⁰. Умножение на j и свидетельствует о том, что вектор напряжения на индуктивности опережает вектор тока на 90⁰.

Мгновенное значение напряжения на ёмкости 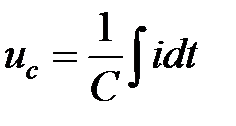заменяется комплексом 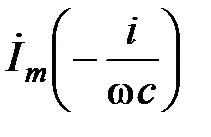, отстающим от тока на 90⁰, что подтверждается наличием вектора -j.

Мгновенное значение ЭДС е - комплексом .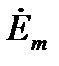

Тогда для схемы на рисунке 3.6 получим уравнение II закона Кирхгофа.

Рис.3.6

Для мгновенных значений

В комплексной форме:

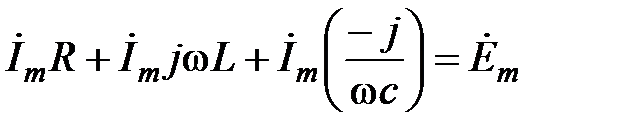(3.6)

Выразим :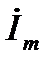

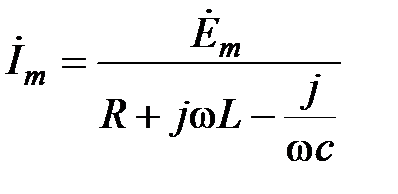(3.7)