Электрическая цепь при параллельном соединении R, L и С

Рассмотрим электрическую цепь с соединёнными параллельно R, C и L элементами (рис.3.16).

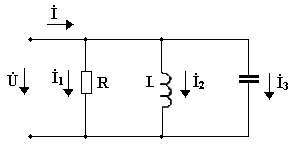
Рис. 3.16

Пусть к данной цепи подводится напряжение 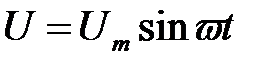, под действием которого в ветвях цепи создаются токи:

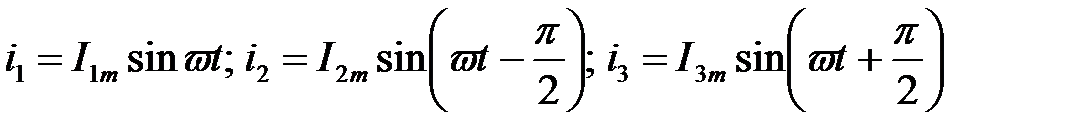
Найдём действующие значения токов схемы на рис. 3.16

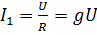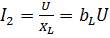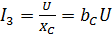; ; ; I

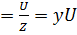
где: 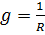– активная проводимость;

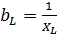– индуктивная проводимость;

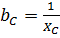– ёмкостная проводимость

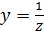– полная проводимость

Запишем I закон Кирхгоффа для данной электрической цепи:

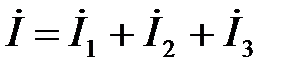
Построим векторную диаграмму токов и напряжений для цепи на рис.3.16. При построении векторной диаграммы токов за начальный удобно взять вектор напряжения, общий для всех ветвей цепи (рис. 3.17)

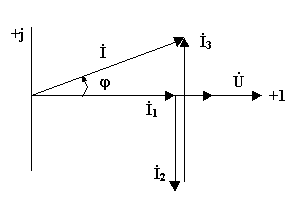
Рис.3.17

Вектор тока 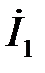совпадает по фазе с вектором 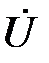, вектор 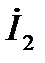отстаёт от вектора 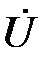на угол 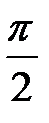, а вектор 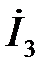опережает вектор 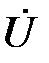на угол 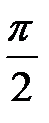. Произведя геометрическое сложение векторов на комплексной плоскости, найдём вектор общего тока .

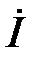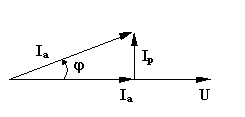
Рис. 3.18

На рис.3.18 построен треугольник токов, катеты которого равны активной 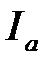и реактивной 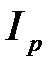составляющим, а гипотенуза полному току I. Активная составляющая тока совпадает по фазе с напряжением; Реактивная составляющая тока 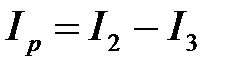сдвинуты по фазе относительно напряжения на угол .

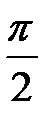Если 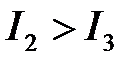, то 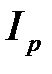отстаёт от U на угол 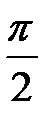, а ток I отстаёт на угол j.

Если 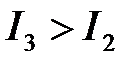, то 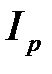опережает U на угол 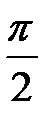, а ток I опережает U на угол j.

Из графика токов (рис.3.18) следует, что ; ;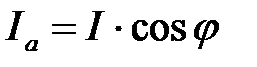

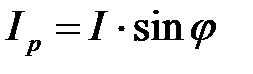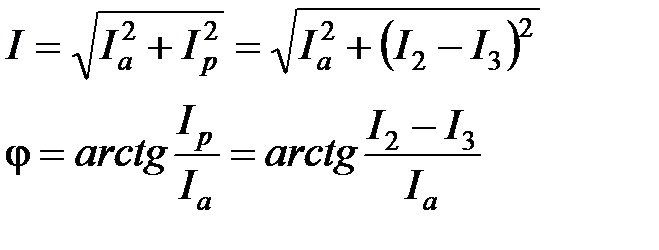
Полная проводимость цепиравна квадратному корню из сумм квадратов активной и реактивной проводимостей.

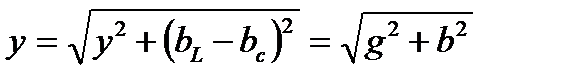
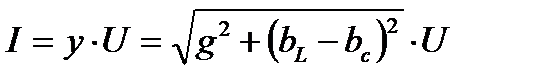
Поделим стороны треугольника токов на напряжение U получим треугольник проводимостей: Из треугольника проводимостей (рис.3.19)

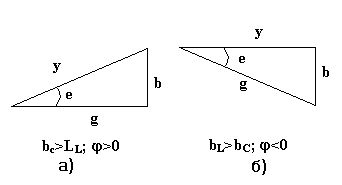
Рис. 3.19

Запишем полную проводимость в комплексной форме:

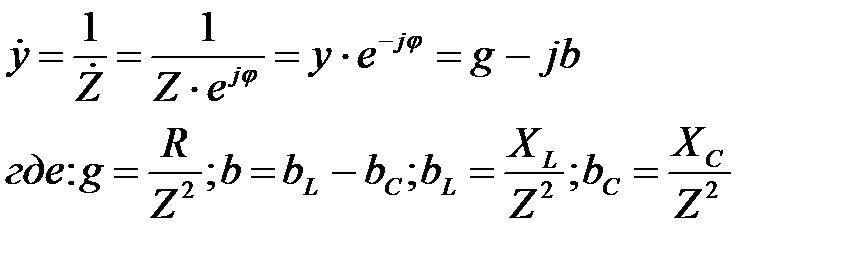
Резонанс токов

Режим работы цепи синусоидального переменного тока, содержащей параллельные ветви с индуктивными и емкостными элементами, когда в результате равенства емкостной и индуктивной проводимостью 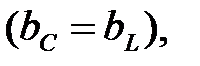ток в неразветвленной части цепи совпадает по фазе с напряжением, называется резонансом токов.

В момент резонанса токов, токи в ветвях с реактивной проводимостью равны между собой и могут превышать полный ток цепи (т.к. токи 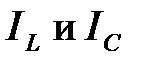находится в противофазе).

Если .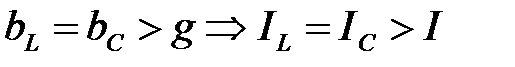

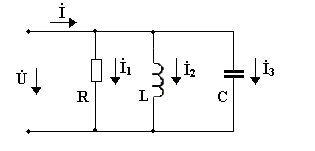
Рис. 3.20

Для схемы на рис.3.20 запишем выражение для тока:

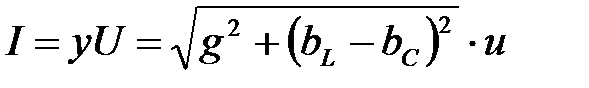
Особый интерес представляет случай когда 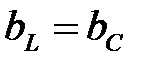. Тогда полная проводимость цепи 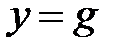, т. к. 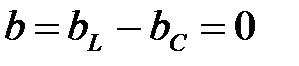, а полный ток 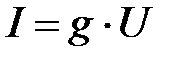имеет минимальное значение и только активную составляющую.

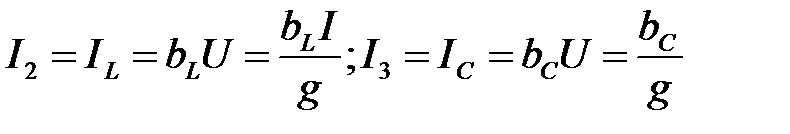
Векторная диаграмма токов для случая резонанса токов представлена на рис.3.21

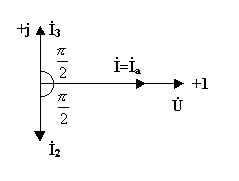
Рис. 3.21

В резонансе токов цепь ведёт себя по отношению к источнику питания как цепь с элементами с активной проводимостью. Через L и С могут протекать токи превышающие ток в источнике питания, но они компенсируют друг друга.

Способы достижения резонанса:

1. Изменение ¦;

2. Изменение L;

3.Изменение C.