Тема 4. Дискретные случайные величины.

4.1. Определение дискретной случайной величины.

Величина, которая в результате испытания может принять то или иное значение, заранее неизвестно, какое именно, называется случайной величиной.

Дискретной случайной величиной называется такая переменная величина, которая может принимать конечную или бесконечную совокупность значений, причем принятие ею каждого из значений есть случайное событие с определенной вероятностью.

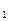Соотношение, устанавливающее связь между отдельными возможными значениями случайной величины и соответствующими им вероятностями, называется законом распределения дискретной случайной величины. Если обозначить возможные числовые значения случайной величины Х через х , х 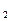, ... ...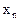, а через 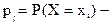вероятность появления значения 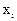, то дискретная случайная величина полностью определяется следующей таблицей 4.1:

Таблица 4.1

			...
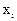
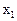
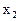
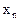
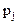
	p1		...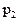

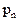
где значения 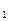х , х 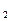,..., ,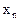записываются, как правило, в порядке возрастания. Таблица называется законом или рядом распределения дискретной случайной величины Х. Поскольку в верхней строчке ряда распределения записаны все значения случайной величины Х, то нижняя строчка обладает тем свойством, что

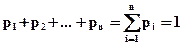(4.1)

Графическое изображение ряда распределения называется многоугольником распределения (полигоном распределения) (рис. 4.1):

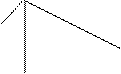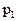
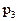
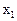
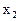
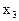
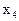
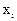
Рис.4.1.

Для этого по оси абсцисс откладывают значения случайной величины, по оси ординат - вероятности значений. Полученные точки соединяют отрезками прямой. Построенная фигура и называется многоугольником распределения вероятностей.

Дискретная случайная величина может быть задана функцией распределения .

Функцией распределения случайной величины Х называется функция F (x), выражающая вероятность того, что Х примет значение, меньшее чем х:

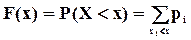(4.2)

- здесь для каждого значения х суммируются вероятности тех значений 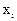, которые лежат левее точки х.

Функция F (x) есть неубывающая функция;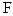

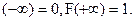
Для дискретных случайных величин функция распределения F(x) есть разрывная ступенчатая функция, непрерывная слева (рис. 4.2):

F(x)

p₃

p₂

p1

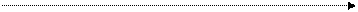x₁ x₂ 0 х₃ x _j

Рис.4.2.

Вероятность попадания случайной величины Х в промежуток от 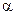до 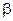(включая 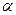) выражается формулой:

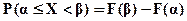(4.3)