Тема 3. ФОРМУЛЫ ПОЛНОЙ ВЕРОЯТНОСТИ И

БАЙЕСА

Часто мы начинаем анализ вероятностей имея предварительные, априорные значения вероятностей интересующих нас событий. Затем из источников информации, таких как выборка, отчет, опыт и т.д. мы получаем дополнительную информацию об интересующем нас событии. Имея эту новую информацию, мы можем уточнить, пересчитать значения априорных вероятностей. Новые значения вероятностей для тех же интересующих нас событий будут уже апостериорными (послеопытными) вероятностями. Теорема Байеса дает нам правило для вычисления таких вероятностей.

Последовательность процесса переоценки вероятностей можно схематично изобразить так:

Априорные Новая информация из Байесовский Апостериорные

вероятности каких-либо источников анализ вероятности

Пусть событие А может осуществиться лишь вместе с одним из событий Н₁, Н₂, Н₃, ..., Н_n, образующих полную группу. Пусть известны вероятности P(H₁), P(H₂),…P(H_i),…P(H_n). Так как события H_i образуют полную группу, то 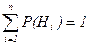.Так же известны и условные вероятности события А: P(A/H₁), P(A/H₂), …P(A/H_i)…, P(A/H_n), i=1, 2, …, n. Так как заранее неизвестно с каким из событий H_i произойдет событие А, то события H_i называют гипотезами.

Необходимо определить вероятность события А и переоценить вероятности событий H_i с учетом полной информации о событии А.

Вероятность события А определяется как:

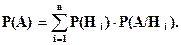(3.1)

Эта вероятность называется полной вероятностью.

Если событие А может наступить только вместе с одним из событий Н₁, Н₂, Н₃, ..., Н_n, образующих полную группу несовместных событий и называемых гипотезами, то вероятность события А равна сумме произведений вероятностей каждого из событий Н₁, Н₂, ..., Н_n на соответствующую условную вероятность события А.

Условные вероятности гипотез вычисляются по формуле:

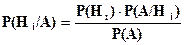
или (3.2)

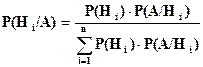
Это - формулы Байеса, (по имени английского математика Т.Байеса, опубликовавшего их в 1764 году) выражение в знаменателе - формула полной вероятности.