Полную группу можно определить так: если
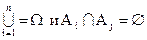 для любой пары (i ¹ j), тогда {A1, A2, … , An} - полная группа событий.
для любой пары (i ¹ j), тогда {A1, A2, … , An} - полная группа событий.
Вероятностью появления события А называют отношение числа исходов, благоприятствующих наступлению этого события, к общему числу всех единственно возможных и несовместных элементарных исходов.
Обозначим число благоприятствующих событию А исходов через М, а число всех исходов - N.
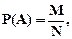
| (2.1) |
где M - целое неотрицательное число,
0 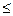 M M 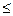 N N
|
Другой тип объективной вероятности определяется исходя из относительной частоты (частости) появления события. Если, к примеру, некоторая фирма в течение времени провела опрос 1000 покупателей нового сорта напитка и 20 из них оценили его как вкусный, то мы можем оценить вероятность того, что потребителям понравится новый напиток как 20/1000=0,02. В этом примере 20 - это частота наступления события, а 20/1000=0,02 - это относительная частота.
Относительной частотой события называется отношение числа испытаний m, при которых событие появилось, к общему числу проведенных испытаний n.
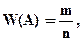
| (2.2) |
где m - целое неотрицательное число,
0 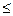 m m 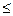 n n
|
Статистической вероятностью события А называется относительная частота (частость) этого события, вычисленная по результатам большого числа испытаний. Будем обозначать её Р*(А). Следовательно, 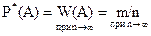 . При очень большом числе испытаний статистическая вероятность приближенно равна классической вероятности, т.е. Р* (A) » Р(A)
. При очень большом числе испытаний статистическая вероятность приближенно равна классической вероятности, т.е. Р* (A) » Р(A)
Для определения вероятности выпадения 1 или 2 при подбрасывании кости нам необходимо только знать “модель игры “, в данном случае - кость с 6 гранями. Мы можем определить наши шансы теоретически, без подбрасывания кости, это - априорная (доопытная) вероятность. Во втором примере мы можем определить вероятность только по результатам опыта, это - апостериорная (послеопытная) вероятность. То есть классическая вероятность - априорная, а статистическая - апостериорная.
Какой бы вид вероятности не был выбран для их вычисления и анализа используется один и тот же набор математических правил.
Свойства вероятности, вытекающие из классического определения.
1. Вероятность достоверного события равна 1, то есть Р( 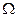 ) = 1.
) = 1.
Действительно, если событие А = 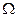 , то M = N, значит Р(
, то M = N, значит Р( 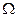 ) = N/N = 1.
) = N/N = 1.
2.Если событие невозможное, то его вероятность равна 0, то есть Р(Æ)= 0.
Если А = Æ, то оно не осуществится ни при одном испытании, то есть M = 0 и Р(Æ) = 0/N = 0.
3.Вероятность случайного события есть положительное число, заключенное между 0 и 1.
В самом деле, та к как 0 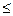 M
M 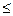 N , то 0
N , то 0 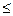 M/ N
M/ N 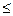 1, то есть 0
1, то есть 0 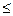 Р(А)
Р(А) 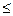 1.
1.
4. Сумма вероятностей противоположных событий равна 1, то есть 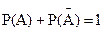 . В самом деле,
. В самом деле, 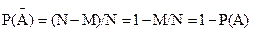
А отсюда:
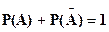
| (2.3) |
Дата добавления: 2016-10-26; просмотров: 1617;











