Зависимые и независимые события
Вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного наступления, то есть:
Р (А+В) = Р(А) + Р(В) - Р(АВ)
или (2.4)
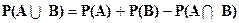
Для несовместных событий их совместное наступление есть невозможное событие Æ, а вероятность его равна нулю. Следовательно, для несовместных событий правило сложения вероятностей принимает следующий вид:
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.
| Для несовместных событий A, B: | |
или 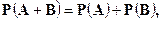 
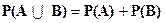
| (2.5) |
Правило сложения вероятностей справедливо и для конечного числа n попарно несовместных событий, то есть:
P(A1+A2+A3+...+An)=P(A1)+P(A2)+P(A3)+...P(An)
или
 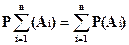
| (2.6) |
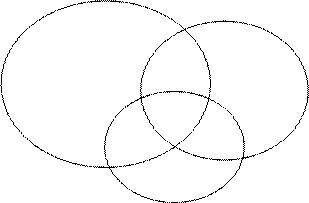
В случае нескольких совместных событий необходимо по аналогии с рассуждениями о пересечении двух совместных событий исключить повторный учет областей пересечения событий. Рассмотрим три совместных события.
 |
| A | AB | B |
| ABC | ||
| AC | C | CB |
Рис. 2.3
Для случая трех совместных событий можно записать:
Р(А + В + С) = Р(А) + Р(В) + Р(С) - Р(АВ) - Р(АС) - Р(ВС) + Р(АВС).
Сумма вероятностей событий А1, А2, А3, ... , Аn, образующих полную группу, равна1, то есть:
P(A1) + P(A2) + P(A3) + ... + P(An) = 1
или
 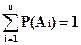
| (2.7) |
Вероятность произведения двух независимых событий А и В равна произведению их вероятностей:
| P(AB) = P(A) × P(B), | |
P(A 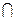 B) = P(A) × P(B) B) = P(A) × P(B)
| (2.8) |
или
События А1, А2, ..., An (n > 2) называются независимыми в совокупности, если вероятность каждого из них не зависит от того, произошли или нет любые события из числа остальных.
Распространим теоремы умножения на случаи n независимых и зависимых в совокупности событий.
Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий.
P(A1 ×A2×A3×…×An) = P(A1)×P(A2) × P(A3) ×…× P(An) (2.9)
Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого:
| Р(АВ) = P(B) × Р(А/В) | (2.10) | |||
Р(А 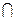 В) = P(B) × Р(А/В) В) = P(B) × Р(А/В)
| ||||
| или Р(АВ) = P(A)×Р(В/А) | ||||
Р(А  В) = Р(A)×(В/А) В) = Р(A)×(В/А)
| ||||
| Вероятность события В при условии появления события А: | ||||
P(B/A) = 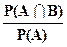 или P(B/A) = или P(B/A) = 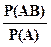
| (2.11) | |||
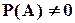 . .
| ||||
Вероятность совместного наступления конечного числа n зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем условная вероятность каждого последующего события вычисляется в предположении, что все предыдущие уже наступили, т.е.
| P(A1 × A2 × A3 ×... ×Аn) = Р(A1) × P(A2 / A1) ×P(A3 / A1 × A2).× . . . ×P(An / A1 × A2 × A3 ×…× An-1) ( 2.12) |
Если события А1, А2, ... An - зависимые в совокупности, то вероятность наступления хотя бы одного из них соответственно равна:
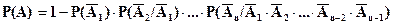 (2.13)
(2.13)

Вероятность появления хотя бы одного события из n независимых в совокупности, равна разности между 1 и произведением вероятностей событий, противоположных данным, то есть:
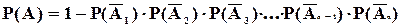 (2.14)
(2.14)
Дата добавления: 2016-10-26; просмотров: 2388;











