Определение вероятности и свойства, вытекающие из её определения. Классификация событий. Диаграммы Венна
Под вероятностью, в широком смысле, понимают количественную меру неопределенности. Это - число, которое выражает степень уверенности в наступлении того или иного случайного события. Например, нас может интересовать вероятность того, что объем продаж некоторого продукта не упадет, если цены вырастут, или вероятность того, что строительство нового дома завершится в срок.
Случайным называется событие, которое может произойти или не произойти в результате некоторого испытания. В дальнейшем для простоты мы будем опускать термин “случайный”.
Мы определим испытание (опыт, эксперимент) как процесс, включающий определенные условия, который приводит к одному из нескольких возможных исходов. Исходом опыта может быть результат наблюдения или измерения. Приведем несколько примеров испытаний и их исходов:
| Испытание | Исход испытания |
| Подбрасывание монеты Контроль качества деталей Продажа квартиры Результат футбольного матча | Цифра, герб Годная, бракованная Продана, не продана Победа, проигрыш, ничья |
Единичный, отдельный исход испытания называется элементарным событием. Случайное событие может состоять из нескольких элементарных событий.
Достоверное событие - это событие, которое обязательно произойдет в результате испытания. Например, если в урне содержатся только белые шары, то извлечение из нее белого шара есть событие достоверное; другой пример, если мы подбросим вверх камень, то он обязательно упадет на Землю в силу действия закона притяжения, то есть результат этого опыта заведомо известен. Достоверные события условимся обозначать символом 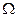 .
.
Невозможное событие - это событие, которое не может произойти в результате данного опыта (испытания). Извлечение черного шара из урны с белыми шарами есть событие невозможное; выпадение выигрыша на все номера облигаций в каком-либо тираже выигрышного займа так же невозможное событие. Невозможное событие обозначим Æ.
Достоверные и невозможные события, вообще говоря, не являются случайными.
Совместные события. Несколько событий называются совместными, если в результате эксперимента наступление одного из них не исключает появления других. Например, при бросании трех монет выпадение цифры на одной не исключает появления цифр на других монетах.
В магазин вошел покупатель. События “в магазин вошел покупатель старше 60 лет” и “в магазин вошла женщина” - совместные, так как в магазин может войти женщина старше 60 лет.
Несовместные события. Несколько событий называются несовместными в данном опыте, если появление одного из них исключает появления других. Например, выигрыш, ничейный исход и проигрыш при игре в шахматы (одной партии) - три несовместных события.
Единственно возможные события. События называются единственно возможными, если в результате испытания хотя бы одно из них обязательно произойдет (или одно, или два, или ... или все события из рассматриваемой совокупности событий произойдут; одно точно произойдет). Например, некоторая фирма рекламирует свой товар по радио и в газете. Обязательно произойдет одно и только одно из следующих событий: “потребитель услышал о товаре по радио”, “потребитель прочитал о товаре в газете”, “потребитель получил информацию о товаре по радио и из газеты”, “потребитель не слышал о товаре по радио и не читал газеты”. Эти четыре события единственно возможные.
Равновозможные события.Несколько событий называются равновозможными, если в результате испытания ни одно из них не имеет объективно большую возможность появления, чем другие. При бросании игральной кости появление каждой из её граней - события равновозможные.
Противоположные события. Два единственно возможных и несовместных события называются противоположными. Купля и продажа определенного вида товара есть события противоположные.
Полная группа событий. Совокупность всех единственно возможных и несовместных событий называется полной группой событий.
Различные события и действия с ними удобно рассматривать с помощью, так называемых, диаграмм Венна (по имени английского математика-логика Джона Венна (1834 -1932)).
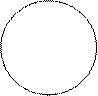
Изобразим полную группу событий в виде квадрата, тогда круг внутри квадрата будет обозначать некоторое событие, скажем А, а точка – элементарное событие – Е.
|
Рис. 2.1
Рисунок 2.1 демонстрирует два противоположных события А и не А, которые дополняют друг друга до полной группы событий. Противоположное событие обозначается - 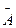
  |
А В
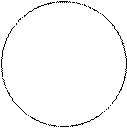
Рис.2.2
Пересечение А и В (обозначается как A 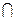 B) есть набор, содержащий все элементы, которые являются членами и А и В.
B) есть набор, содержащий все элементы, которые являются членами и А и В.
Объединение А и В (обозначается A 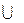 B) есть набор, содержащий все элементы, которые являются членами или А, или В, или А и В вместе.(рис. 2.2)
B) есть набор, содержащий все элементы, которые являются членами или А, или В, или А и В вместе.(рис. 2.2)
Дата добавления: 2016-10-26; просмотров: 2205;

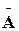
 · Е а
· Е а









