ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

Итак, мы получили меру отклонения по результатам n опытов: среднее арифметическое квадратов отклонений

=

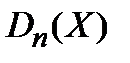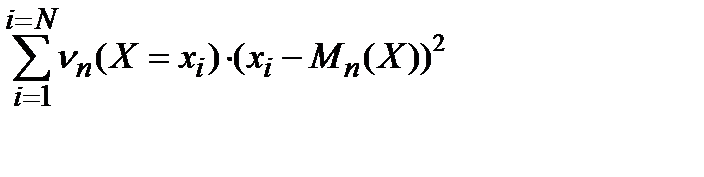
Но полученное значение может отличаться при повторениях серий из n опытов, а желательно иметь стабильное значение величины, описывающей разброс значений случайной величины.

Искомая стабильная величина получается при неограниченном увеличении числа опытов. Название у неё будет: дисперсия – рассеяние.

При возрастании количества опытов n частоты отдельных значений стремятся к их вероятностям, т.е. к значениям закона распределения.

,

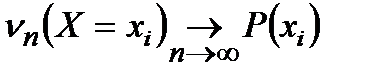среднее арифметическое – к математическому ожиданию

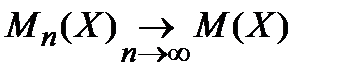
Соответственно, выражение для среднего арифметического квадратов отклонений изменится так

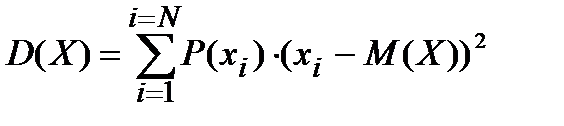
В этом выражении вместо частот стоят значения закона распределения, а возле обозначения дисперсии D буква n уже не пишется.

N (эн большое) – это, по-прежнему, количество возможных значений.

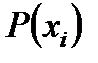– значения закона распределения дискретной случайной величины (вероятности отдельных возможных значений x_i случайной величины).

В теории вероятности дисперсия дискретной случайной величины вычисляется без проведения каких-либо опытов, если известны значения закона распределения.

Таким образом, дисперсия дискретной случайной величины вычисляется как средний квадрат отклонения значений случайной величины от математического ожидания.

На обиходе столь же часто пользуются и другой мерой рассеяния, которую находят как квадратный корень из дисперсии:

.

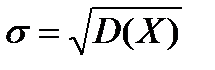Она носит название среднеквадратическое отклонение (илистандартное отклонение).

Если s возвести в квадрат, то получится – 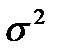. Она же – дисперсия. Таким образом, получается, что для дисперсии можно использовать два обозначения: D(X) и 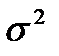, т.е.

D(X) = .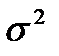

Если единицы измерения случайной величины X обозначить «е.и.», то и матожидание измеряется также в «е.и.».

Единица измерения дисперсии – квадрат размерности случайной величины, т.е. «е.и.²», а среднеквадратическое отклонение – снова в «е.и.». В этом его удобство.