СИММЕТРИЧНЫЕ ИНТЕРВАЛЫ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ

Нормальное распределение, как это можно видеть из математической записи, зависит только от двух параметров: математического ожидания m и дисперсии s².

Существует даже специальное краткое обозначение плотности вероятности нормального распределения, отражающее этот факт:

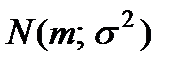
Изобразим на рисунке плотность вероятности нормальной случайной величины Х с заданными математическим ожиданием m и дисперсией .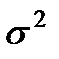

x

m

m–2s

m+s

m+2s

m–s

m+3s

m–3s

P(«±s»)=0,682

P(«±2s») = 0,955

P(«±3s») = 0,997

N(m;s 2)

S= 0,682

На горизонтальной оси отметим точку математического ожидания.

Если дана дисперсия s ², то значит можно извлечь из неё квадратный корень и получить среднеквадратическое отклонение s .

Отложим обе стороны от точки математического ожидания расстояния в одну «сигму».

Получим точку m–s и точку m+s.

Эта пара точек образует интервал, симметричный относительно плотности нормального распределения.

Вероятность того, что нормальная случайная величина Х примет значение в пределах интервала от m–s до m+s, равна, как точно вычислили математики, – 0,682.

P( m–s £ Х < m+s) = 0,682

Что это за значение 0,682. Это площадь под центральной частью кривой.

А под всей кривой, помним, площадь – единица.

Теперь отложим от математического ожидания уже по две «сигме» в каждую сторону.

Получим точки m–2s и m+2s.

Вероятность того, что нормальная случайная величина Х примет значение в пределах от m–2s до m+2s , равна – 0,955.

P( m–2s £ Х < m+2s) = 0,955

И, наконец, отложим по три «сигмы».

Получим точки m–3s и m+3s.

Вероятность того, что нормальная случайная величина Х примет значение в пределах от m–3s до m+3s , равна – 0,997.

P( m–3s £ Х < m+3s) = 0,997

Каждая рассмотренная пара точек образует интервал, симметричный относительно плотности нормального распределения.

0,682; 0,955 и 0,997 – это вероятности попадания в симметричные интервалы, соответствующие однократному, двукратному и трёхкратному отклонениям.

Смыслы интервалов с точки зрения попадания в них случайной величины таковы:

в интервал по однократному отклонению – попадает большинство;

по двукратному – попадает подавляющее большинство;

по трёхкратному – попадают практически все.

Наиболее используемым и поэтому известным является интервал трёхкратного отклонения.

В него в среднем попадает 99,7 % всех значений, т.е. в среднем НЕ попадают только 3 из 1000.

В статистическом обиходе даже имеется так называемое «правило 3-х сигм»:

в интервал плюс минус 3 сигмы от математического ожидания в среднем попадает 99,7 % значений нормальной случайной величины.

Собственного названия рассмотренные интервалы не имеют. Однако в задачах управления качеством выпускаемой продукции эти интервалы именуются интервалами допуска.

Например, автоматическая линия выпускает изделия со средним значением какого-либо показателя (вес изделия, диаметр, концентрация) равным m.

У каждого отдельного изделия этот показатель может быть чуть больше или чуть меньше среднего, но не намного.

Изредка с конвейера сходят изделия с большими отклонениями показателя от среднего значения.

Они должны отбраковываться.

Для отбраковки устанавливается некоторый интервал [m–Dx/2; m+Dx/2].

Попадание значения показателя изделия в его пределы означает приёмку этого изделия. Выход же за пределы этого интервала означает недопуск изделия.

Поэтому такой интервал называется интервалом допуска.

Если в брак идёт слишком много изделий, то надо останавливать автоматическую линию и заниматься её настройкой. Надо сделать так, чтобы среднее значение выпускаемых изделий было ближе к m, т.е. к центру интервала допуска, а разброс показателя s был как можно меньше.

Тема 8.
ВЫБОРОЧНЫЙ МЕТОД

Мы с вами знаем, что статистика – это область знаний о правилах сбора и приёмах обработки данных, получаемых в ходе наблюдений за явлениями, сущность которых известна отчасти или почти не известна, т.е. за случайными явлениями.

Изучением правовых явлений занимается правовая статистика, и использует она при этом такой раздел математики как аналитическая статистика.

Аналитическая статистика занимается обработкой собранных числовых данных безотносительно к их природе.

Обработка необходима потому, что данные, как правило, представляют собой большие массивы чисел, даже обозреть которые бывает достаточно трудно.

Данные в массивах «скачут» непонятным образом.

Вместе с тем по этим массивам нужно делать выводы, например:

«Каково среднее значение?»,

«Каков разброс?»,

«Наблюдается ли на фоне скачков рост или спад, и какова его скорость?»

«Есть ли взаимозависимость между данными из двух различных массивов?»

«Два массива данных получены при наблюдении одного и того же явления или разных?»

и т.д.

И, наконец, самое важное о статистике.

Статистика не даёт понимания сущности явления, данные которого с её помощью обрабатываются.

Исследованием сущности занимаются предметные науки, которые и используют результаты статистики.

Но это не принижает её роли, т.к. без статистики они не смогли бы сделать многих своих выводов о сущности изучаемого явления.

Таким образом, наша задача познакомиться с тем, как обрабатываются собранные статистические данные.

Аналитическая статистика опирается на понятия теории вероятности.

Как мы помним, задача теории вероятности состоит в том, чтобы на основе знания вероятностных характеристик случайной величины предсказать исход сложного опыта или серии опытов с ней.

Выборочный метод аналитической статистики решает обратную задачу:

по исходам серии опытов указать или оценить значения вероятностных характеристик случайной величины.