Размещения с повторениями
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Для успешного решения задач с использованием классического определения вероятности необходимо знать основные правила и формулы комбинаторики.
Комбинаторика происходит от латинского слова ”combinatio” соединение.
Группы, составленные из каких-либо предметов, (безразлично каких, например, букв, цветных шаров, кубиков, чисел и т.п.), называются соединениями (комбинациями).
Предметы, из которых состоят соединения, называются элементами.
Различают три типа соединений: перестановки, размещения и сочетания.
Размещения
Размещениями из n элементов по m в каждом называются такие соединения, каждое из которых содержит m элементов, взятых из числа данных n элементов, и которые отличаются друг от друга либо самими элементами (хотя бы одним), либо лишь порядком их расположения.
Число размещений из n элементов по m в каждом обычно обозначается символом 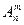 и вычисляется по формуле (1.1)[1]:
и вычисляется по формуле (1.1)[1]:
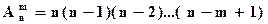 . .
| (1.1) |
Понятие факториала
Произведение n натуральных чисел от 1 до n обозначается сокращенно n!, то есть 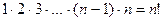 (читается: n факториал).
(читается: n факториал).
Например, 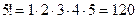 .
.
Считается, что 0! = 1.
Используя понятие факториала, формулу (1.1) можно представить так:
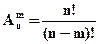 , ,
| (1.2) |
где 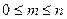 .
.
Очевидно, что 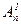 = n (при m=1) и
= n (при m=1) и 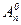 = 1 (при m=0).
= 1 (при m=0).
Размещения с повторениями
Размещение с повторениями из n элементов по m(m × n) элементов может содержать любой элемент сколько угодно раз от 1 до m включительно, или не содержать его совсем, то есть каждое размещение с повторениями из n элементов по m элементов может состоять не только из различных элементов, но из m каких угодно и как угодно повторяющихся элементов.
Соединения, отличающиеся друг от друга хотя бы порядком расположения элементов, считаются различными размещениями.
Число размещений с повторениями из n элементов по m элементов будем обозначать символом 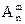 (c повт.)
(c повт.)
Можно доказать, что оно равно nm.
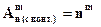
| (1.3) |
Сочетания
Сочетаниями из n элементов по m в каждом называются такие соединения, каждое из которых содержит m элементов, взятых из числа данных n элементов, и которые отличаются друг от друга по крайней мере одним элементом.
Число сочетаний из n элементов по m в каждом обозначается символом 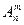 и вычисляется так:
и вычисляется так:
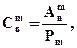 где
где 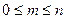 , ,
| (1.4) |
или
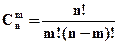 где
где 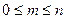 . .
| (1.5) |
Свойства сочетаний:
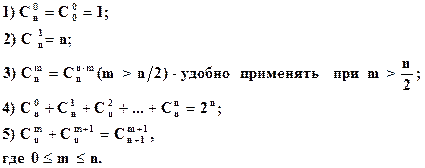
|
Дата добавления: 2016-10-26; просмотров: 5028;











