Выборка с повторениями
Пусть имеется выборка из 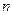 элементов, причем
элементов, причем 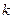 элементов из них - одинаковые.
элементов из них - одинаковые.
1. Число различных перестановок на элементах такой выборки равно:
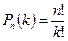 - число перестановок с
- число перестановок с 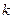 повторениями на множестве из
повторениями на множестве из 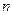 элементов
элементов
2. Сочетание с повторениями из 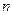 элементов по
элементов по 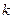 - неупорядоченная выборка
- неупорядоченная выборка 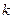 элементов с возвращением из множества, содержащего
элементов с возвращением из множества, содержащего 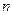 элементов:
элементов:
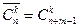 - число различных сочетаний с повторениями из
- число различных сочетаний с повторениями из 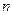 элементов по
элементов по 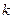
3. Размещения с повторениями из 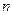 элементов по
элементов по 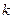 - расположение
- расположение 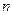 различных шаров по
различных шаров по 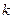 различным ячейкам
различным ячейкам
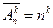 - число различных размещений с повторениями
- число различных размещений с повторениями
Определение. Сочетаниями из 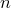 различных элементов по
различных элементов по 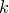 элементов называются комбинации, которые составлены из данных
элементов называются комбинации, которые составлены из данных 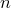 элементов по
элементов по 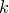 элементов и отличаются хотя бы одним элементом (иначе говоря,
элементов и отличаются хотя бы одним элементом (иначе говоря, 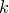 -элементные подмножества данного множества из
-элементные подмножества данного множества из 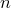 элементов).
элементов).
Как видим, в сочетаниях в отличие от размещений не учитывается порядок элементов. Число всех сочетаний из 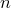 элементов по
элементов по 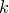 элементов в каждом обозначается
элементов в каждом обозначается 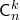 (от начальной буквы французского слова “combinasion”, что значит “сочетание”).
(от начальной буквы французского слова “combinasion”, что значит “сочетание”).
Числа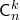
Все сочетания из множества 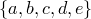 по два —
по два — 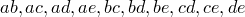 .
.
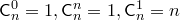 .
.
Свойства чисел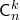
1. 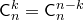 .
.
Действительно, каждому 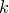 -элементному подмножеству данного
-элементному подмножеству данного 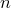 элементного множества соответствует одно и только одно
элементного множества соответствует одно и только одно 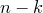 -элементное подмножество того же множества.
-элементное подмножество того же множества.
2. 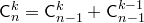 .
.
Действительно, мы можем выбирать подмножества из 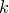 элементов следующим образом: фиксируем один элемент; число
элементов следующим образом: фиксируем один элемент; число 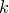 -элементных подмножеств, содержащих этот элемент, равно
-элементных подмножеств, содержащих этот элемент, равно 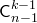 ; число
; число 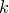 -элементных подмножеств, не содержащих этот элемент, равно
-элементных подмножеств, не содержащих этот элемент, равно 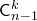 .
.
Бином Ньютона. Это формула, представляющая выражение ( a + b ) n при положительном целом n в виде многочлена:
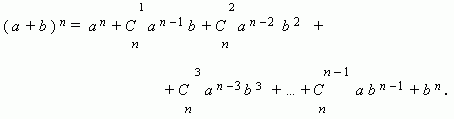
Заметим, что сумма показателей степеней для a и b постоянна и равна n.
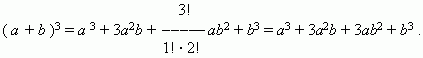
Дата добавления: 2017-05-02; просмотров: 2170;











