Уравнение Шредингера. Волновая функция
Состояние микрочастицы в квантовой механике характеризуется так называемой волновой функцией, обозначаемой буквой Y (пси). Вид этой функции получается из решения уравнения Шредингера, которое выглядит следующим образом:
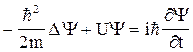 . (26)
. (26)
Здесь m - масса частицы, U – ее потенциальная энергия, i – мнимая единица,
D – оператор Лапласа, Y = Y(x,y,z,t) – функция координат и времени.
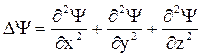 . (27)
. (27)
Если силовое поле, в котором движется частица, стационарно, т.е. U не зависит явно от времени, то уравнение (26) переходит в более простое уравнение Шредингера для стационарных состояний:
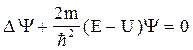 . (28)
. (28)
Здесь Y = Y(x,y,z) – функция координат.
Решения данного уравнения и рассматривает квантовая механика.
Правильную интерпретацию смысла волновой функции дал М. Борн в 1926 г. Согласно Борну квадрат модуля волновой функции дает плотность вероятности нахождения частицы в соответствующем месте пространства.
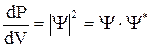 . (29)
. (29)
В соответствии с этим для волновой функции должно выполняться условие нормировки
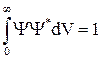 . (30)
. (30)
В соответствии со своим смыслом волновая функция должна быть однозначной, конечной, непрерывной и иметь непрерывную и конечную производную. Совокупность этих требований носит название стандартных условий.
Уравнение Шредингера имеет решения, удовлетворяющие стандартным условиям, лишь при некоторых избранных значениях параметра Е (т.е. энергии). Эти избранные значения называются собственными значениями энергии. Решения, соответствующие собственным значениям Е, называютсясобственными функциями частицы. Совокупность собственных значений называется энергетическим спектром. Он может быть дискретным или сплошным. В случае дискретного спектра собственные значения и собственные функции можно пронумеровать:
E1, E2, ... En, ...; (31)
Y1, Y2, ... Yn, ... .
Нахождение собственных значений энергии и собственных функций частиц является основной задачей квантовой механики.
Дата добавления: 2016-10-26; просмотров: 2006;











