Теорема сложения вероятностей.

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

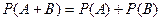или

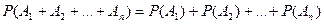
Следствие 1. Если событие А₁, А₂, … ,А_n образуют полную систему, то сумма вероятностей этих событий равна единице.

.

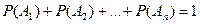Следствие 2. Сумма вероятностей противоположных событи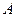й и 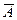равна единице.

.

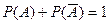Задача 1. Имеется 100 лотерейных билетов. Известно, что на 5 билетов попадает выигрыш по 20000 руб., на 10 - по 15000 руб, на 15 - по 10000 руб., на 25 - по 2000 руб. и на остальные ничего. Найти вероятность того, что на купленный билет будет получен выигрыш не менее 10000 руб.

Решение. Пусть А, В, и С- события, состоящие в том, что на купленный билет падает выигрыш, равный соответственно 20000, 15000 и 10000 руб. так как события А, В и С несовместны, то

.

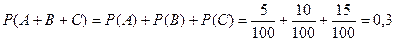Задача 2. На заочное отделение техникума поступают контрольные работы по математике из городов А, В и С. Вероятность поступления контрольной работы из города А равна 0,6, из города В - 0,1. Найти вероятность того, что очередная контрольная работа поступит из города С.

Решение. События «контрольная работа поступила из города А», «контрольная работа поступила из города В» и «контрольная работа поступила из города С» образуют полную систему, поэтому сумма их вероятностей равна единице:

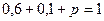, т.е. .

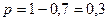Задача 3. Вероятность того, что день будет ясным, 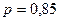. Найти вероятность 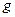того, что день будет облачным.

Решение. События «день ясный» и «день облачный» противоположные, поэтому

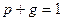, т.е .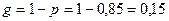

Дискретная и непрерывная случайные величины .Закон распределения случайной величины Нахождение математического ожидания. Дисперсия и среднеквадратичное отклонение дискретной случайной величины, заданной законом распределения