Среднее квадратичное отклонение и дисперсия случайной величины.
Пример 2. Найдем математическое ожидание случайных величин 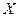 и
и 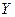 , зная законы их распределения
, зная законы их распределения
1)
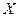
| -8 | -4 | -1 | |||
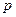
| 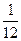
| 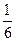
| 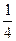
| 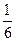
| 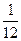
| 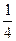
|
2)
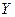
| -2 | -1 | ||||
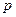
| 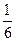
| 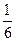
| 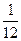
| 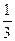
| 
| 
|
Решение:
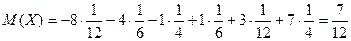 ,
,
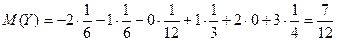 .
.
|
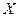 и
и 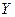 разные, а их математические ожидания одинаковы.
разные, а их математические ожидания одинаковы.

|
Из рисунка б видно, что значение величины 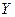 более сосредоточены около математического ожидания
более сосредоточены около математического ожидания 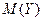 , чем значения величины
, чем значения величины 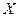 , которые разбросаны (рассеяны) относительно ее математического ожидания
, которые разбросаны (рассеяны) относительно ее математического ожидания 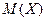 (рисунок а).
(рисунок а).
Основной числовой характеристикой степени рассеяния значений случайной величины 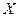 относительно ее математического ожидания
относительно ее математического ожидания 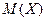 является дисперсия, которая обозначается через
является дисперсия, которая обозначается через 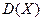 .
.
Определение. Отклонением называется разность между случайной величиной 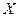 и ее математическим ожиданием
и ее математическим ожиданием 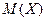 , т.е.
, т.е. 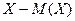 .
.
Отклонение 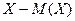 и его квадрат
и его квадрат 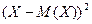 также являются случайными величинами.
также являются случайными величинами.
Определение. Дисперсией дискретной случайной величины 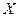 называется математическое ожидание квадрата ее отклонения:
называется математическое ожидание квадрата ее отклонения:
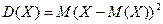 .
.
Свойства дисперсии.
1. Дисперсия постоянной величины С равна 0:
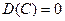 .
.
2. Если 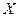 - случайная величина, а С – постоянная, то
- случайная величина, а С – постоянная, то
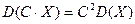
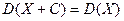 .
.
3. Если 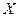 и
и 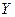 - независимые случайные величины, то
- независимые случайные величины, то
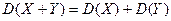 .
.
Для вычисления дисперсий более удобной является формула
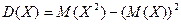 .
.
Пример 3. Дискретная случайная величина распределена по закону:
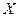
| -1 | |||
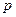
| 0,2 | 0,1 | 0,3 | 0,4 |
Найти 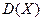 .
.
Решение. Сначала находим 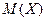 .
.
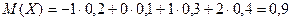 ,
,
а затем 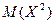 .
.
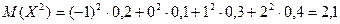 .
.
По формуле 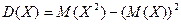 имеем
имеем
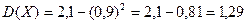 .
.
Средним квадратичным отклонением случайной величины называется корень квадратный из ее дисперсии:
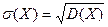 .
.
Дата добавления: 2021-01-26; просмотров: 501;











