АВТОМАТЫ КАК ДИНАМИЧЕСКИЕ СИСТЕМЫ

Примером конкретной динамической системы является логический автомат [2,20,26]:

А = [X; Y; S; d; l],

X - множество входных слов; Y - множество выходных слов; S - множество слов, характеризующих внутреннее состоя­ние автомата; d, l - характеристические функции: d - функция переходов, l - функция выходов.

Время здесь вводится как система тактовых импульсов, по­даваемых извне: t_n+1 = t_n + Dt, Dt - межтактовый интервал; n - обозначение те­кущего такта; n + 1 - последующего.

Автомат - это с одной стороны устройство, а с другой - ма­тематическая модель поведения логического объекта с памятью или без нее. Как устройство автомат способен выполнять определенные функции без вмешательства человека или при ограниченном его участии. Как математическая модель автомат отражает физические или абстрактные явления самой разнообразной природы ( в тех­нике, психологии, лингвистике, управлении ...).

Поведение логического автомата определяется двумя функ­циями:

d: X ´ S ® S - функцией переходов (по типу отображения j в общей динамической системе);

l : X ´ S ® Y - функцией выходов (аналог h).

Работа конечных логических автоматов определяется тремя множествами : Х;S;Y.

Мощности этих множеств определяют понятие (p,q,r) - ав­томата: p = ½Х½; q = ½Y½; r = ½S½.

Варианты схем, описывающих логический автомат, пред­ставлены в литературе [2,20].

Если длина слов соответственно n, m, k, то имеем p = p_iⁿ, q = q_i^m, r = r_i^k .

Здесь p_i , q_i , r_i - число символов алфавита [2].

Размерность таблиц функций d и l одинакова и равна
½Х½ ´ ½S½ = р ´ q = р_iⁿ ´ q_i^m , т.е. определяется длиной слова (n ´ m) и набора символов в алфавите (р_i и q_i).

Упражнения

1. Определите соответствие знаковых систем, описывающих общую динамическую систему и логический автомат.

2. На множествах X = {0, 1, 2, 3}, Y = {0, 1} и S = {0, 1, 2, 3} задайте по своему усмотрению таблицы d и l, как алгебраические операции.

а. Определите длину слов n, m и k при переходе к двузнач­ной системе исчисления слов.

б. Определите параметры (p, q, r) - автомата в данном кон­кретном случае.

в. Постройте карту Карно для логической схемы автомата и определите необходимое число элементов задержки.

2. Создайте схему устройства, поведение которого анало­гично математическому описанию автомата.

ЭМПИРИЧЕСКИЕ СИСТЕМЫ

ИСХОДНАЯ СИСТЕМА

Исходная система (I) рассматривается как промежуточная между системой данных (D) и объектом наблюдений (Ъ).

Согласно системному подходу объект наблюдений пред­ставляется в виде систем.

Процесс перехода от Ъ к I включает систему преобразова­ний и действий субъекта, основу которых составляют неформаль­ные операции семантического характера.

Согласно системологии Клира система I может быть описа­на как алгебраическая структурам [1]:

I = (I_c; I_k; I_a; Q; E), где I_c; I_k; I_a – множества; (6. 1)

Q, Е - отношения операционного типа, называемые кана­лами наблюдений и абстрагирования соответственно.

Систему (6.1) можно представить в развернутом виде (см. рис. 6.1).

Рассмотрим составляющие исходной системы.

Субъект, наблюдая объект, выделяет свойства {(а_i; А_i)} и параметры {(b_j, В_j)} наблюдений, прообразы переменных и баз.

Например а) посещаемость и успеваемость студента в зада­че "Учебный процесс"; б) токи и напряжения в физическом экс­перименте ...

Каналом наблюдений может быть сам наблюдатель, система измерений и управления экспериментом, и ряд других средств. Канал наблюдений может быть четким (Q) и нечетким ( 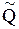) по характеру получаемой информации:

Q = ({a_i: А_i ® V_i}; {b_j: B_j ® W_j }). (6.2)

iÎN_n = {1,2,3,...,n};

jÎN_m = {1,2,3,...,m}.

Для нечеткого канала наблюдений имеем:

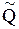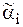= ({ : A_i ´ V_i ® [0; 1]}; {b_j: B_j ´ W_j }). (6.3)

Базис в обоих случаях определяется изначально как четкое соответствие.

Обобщение получаемых данных ведется по каналу абстра­гирования (g^-1; d^-1) и конкретизации (g; d):

Е = ({g_i: 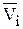® V_i }; {d_j: 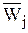® W_j }). (6.4)

Для двухшаговой операции абстрактная система I_a опреде­ляется композицией функций :

I_a = ({А_i; 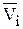; a_i о g_j^-1 }; {d_j; 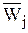® W_j }) (6.5)

Особенность создания исходной системы I = (I_c;I_k;I_a) состо­ит в том, что она определяется на дометодологическом уровне, где человеческий фактор (интуиция, эвристика, логика) играют определяющую роль. Это творческий процесс порождения новых данных и задач,

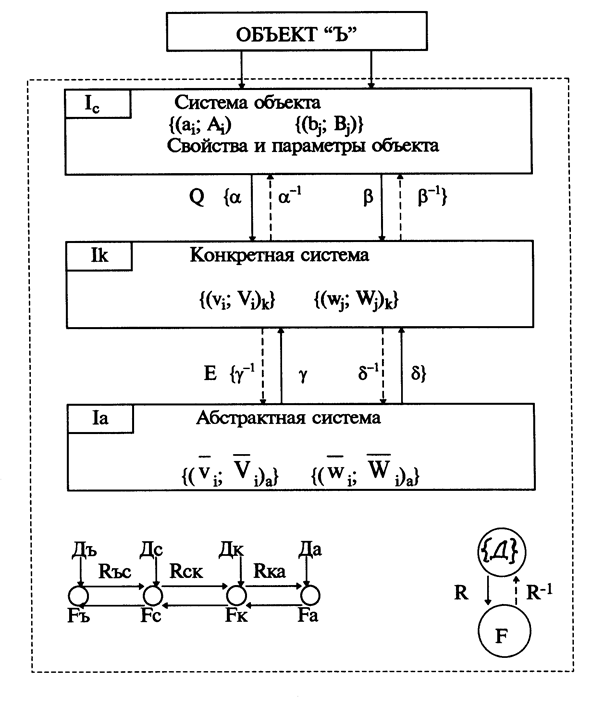
Рис. 6.1. Исходная система:

I = ((I_c; I_k; I_a); (Q; E))

корректировка новых целей исследований на ос­нове полученных субъектом данных и знаний.

Упражнения

Выделите исходную систему и проведите структуризацию ее составляющих (согласно схеме рис . 6.1) для следующих объектов:

1. Объект физической природы (П.1).

2. Объект социальной природы (П.2).

3*. Реальная система массового обслуживания [20].

4*. Система двух сигналов [58].

5*. Объект, определяемый программой единичного экспе­римента [60, с.25].

*) По указанным первоисточникам.

СИСТЕМА ДАННЫХ

Исходная система I определяет нулевой уровень системологического анализа объекта, как комплекса систем I_C, I_К, I_А.

На нулевом уровне конкретизируется значение полного па­раметра базирования :

W Í W₁ ´ W₂ ´ ... ´ W_m = {(w₁ ; w₂; ... w_m )},

формируется описание полного состояния переменных:

V Í V₁ ´ V₂ ´ ... ´ V_n = {(v₁ ; v₂; ... v_n )}.

Исходная система в итоге имеет вид (по определению) :

опр

I = (V, W) Û D_0.

По сути определено множество элементов по переменным и базам, образующих начальную систему данных наблюдений (D₀). Для формирования системы данных необходимо выделить отно­шения вида W ® V , т.е. упорядочить систему I, задав это отношение

d: W ® V, d Î D. (6.6.)

Упорядоченная система по d называется системой данных:

D = (V, W, d) = (I, d), (6.7.)

где (V, W) - элементы системы; d - отношения между эле­ментами.

Система данных D порождается субъектом заданием от­ношения d.

Выше приведено формальное определение системы данных.

Для систем данных, связанных с семантическими опера­циями (с семантикой), область описания D расширяется за счет включения в систему соответствующих правил вывода:

Ds = (S, d), (6.8)

где Ds - система данных с семантикой.

Методологически системы данных могут быть организова­ны как нейтральные или направленные системы, с семантикой или без нее: D, Ds, , .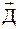

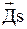Для нечетких каналов наблюдений в систему данных вво­дится мера нечеткости:

р_i: Vi ® [0,1], i Î N_n ,

где р_i = П р_i (р₁; р₂; ...р_i;...р_n).

å р_i = 1; 0 £ р_i £ 1.

Нечеткость определяется как семантика модальности (возможно, вероятно, доверительно...).

Нечеткости описываются функциями, задаваемыми на уни­версальном отрезке (универсуме):

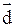: W® , w 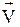Î W, 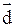(w) = p;

p = (р₁; р₂;…р_n) Î V; р Î [0;1].

Классы нечетких мер можно определить в виде отношений на универсуме "С" из понятий , определяемых в виде системы высказываний:

С - универсум класса нечетких мер;

X₁ Ì С - меры правдоподобия;

X₂ Ì С - меры доверия ( убежденности );

С = X₁ È Х₂; Х₁ Ç Х₂ ¹ Æ.

Х₁ Ç Х₂ = Р - вероятностные меры;

Х₃ - возможностные меры: X₃ Ì X₁;

Х₄ - четкая возможность: X₄ Ì X₃;

Х₅ - меры необходимости: X₅ Ì X₂;

Х_б - четкая необходимость (уверенность): X₆ Ì X₅;

Общая система отношений имеет вид:

X₆ Ì X₅ Ì X₂ Ì C = X₁ È Х₂;

X₄ Ì X₃ Ì X₁ Ì C; X₁ Ç Х₂ = P.

Упражнения

1. Постройте диаграмму Эйлера для классов нечетких мер.

2. Определите систему данных в задачах, задавшись поняти­ем "исходная система":

а) два сигнала;

б) учебный процесс;

в) G/G/3/3.