Формула Ньютона – Лейбница
Если 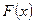 есть какая-либо первообразная от непрерывной функции
есть какая-либо первообразная от непрерывной функции 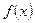 , то справедлива формула
, то справедлива формула
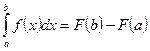 .
.
Она называется формулой Ньютона – Лейбница или основной формулой интегрального исчисления. Эта формула дает практически удобный метод вычисления определенных интегралов в том случае, если известна первообразная подынтегральной функции.
Пример 1.Вычислить интеграл 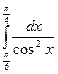 .
.
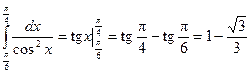 .
.
Пример 2.Вычислить интеграл 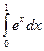 .
.
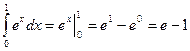 .
.
Пример 3.Вычислить интеграл 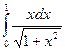 .
.
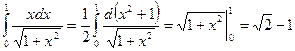 .
.
Простейшие методы вычисления определенных интегралов
Замена переменной в определенном интеграле
Пусть дан интеграл
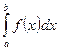 ,
,
где функция 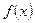 непрерывна на отрезке
непрерывна на отрезке 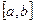 . Введем новую переменную t формулой
. Введем новую переменную t формулой
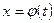 .
.
Если
1) 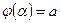 ,
, 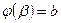 ;
;
2) 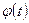 и
и 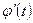 непрерывны на отрезке
непрерывны на отрезке 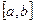 ;
;
3) 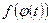 определена и непрерывна на отрезке
определена и непрерывна на отрезке 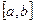 , то
, то
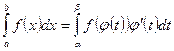 .
.
Отметим, что при вычислении определенного интеграла в данном случае мы не возвращаемся к старой переменной.
Пример 4.Вычислить интеграл 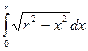 .
.
Сделаем замену переменной 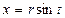 , тогда
, тогда 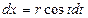 . Определим новые пределы:
. Определим новые пределы: 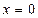 при
при 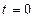 ,
, 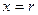 при
при 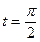 . Следовательно,
. Следовательно,
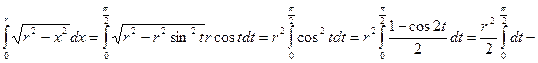
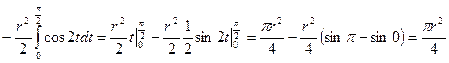 .
.
Пример 5.Вычислить интеграл 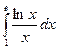 .
.
Сделаем замену переменной 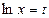 ,
, 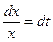 . Определим новые пределы:
. Определим новые пределы: 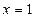 при
при 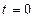 ,
, 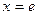 при
при 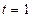 . Следовательно,
. Следовательно,
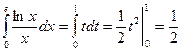 .
.
Дата добавления: 2021-01-26; просмотров: 466;











