Теорема существования определенного интеграла

Вычисление определенного интеграла

Мощным средством исследования в математике, физике, механике и других дисциплинах является определенный интеграл – одно из основных средств математического анализа. Вычисление площадей, ограниченных кривыми, длин дуг, объемов, работы, скорости, пути, моментов инерции и т.д. сводится к вычислению определенного интеграла.

Пусть на отрезке [a, b] задана непрерывная функция 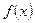. Разделим отрезок 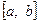на п произвольных частей точками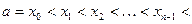 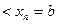, выберем на каждом элементарном отрезке 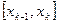произвольную точку 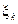и найдем длину каждого такого отрезка: .

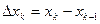Определение 1.Интегральной суммой для функции 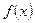на отрезке 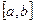называется сумма следующего вида ,

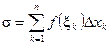Определение 2.Определенным интегралом от функции 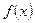на отрезке 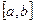(или в пределах от а до b) называется предел интегральной суммы (если он существует) при условии, что длина наибольшего из элементарных отрезков ( 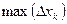) стремится к нулю:

.

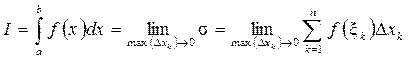Теорема существования определенного интеграла

Если функция 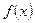непрерывна на отрезке 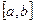, то предел интегральной суммы существует и не зависит от способа разбиения отрезка 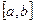на элементарные отрезки и от выбора точек .

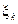При этом числа а и b соответственно называются нижним и верхним пределами интегрирования.

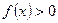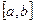Если на , то определенный интеграл 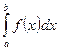с геометрической точки зрения представляет собой площадь криволинейной трапеции – фигуры, ограниченной линиями 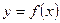, , 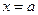, 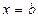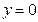(рис. 1).

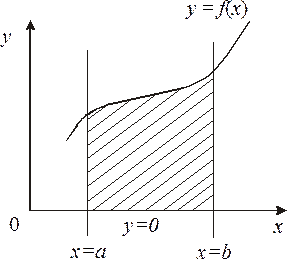Рис. 1

Приведем далее без доказательства основные свойства определенного интеграла, непосредственно вытекающие из определения:

1. ;

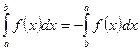2. ;

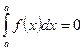3. ;

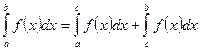4. ;

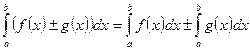5. 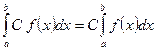, где С – постоянная величина;

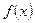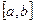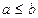6. Оценка определенного интеграла. Если т и М – наименьшее и наибольшее значения функции на отрезке и , то

;

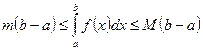7. Если на отрезке 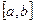функци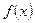и и 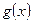удовлетворяют условию 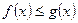, то

;

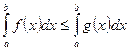8.Теорема о среднем. Если функция 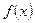непрерывна на 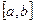, то на этом отрезке имеется такая точка x, что справедливо следующее равенство:

.

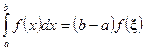Рассмотрим правила вычисления определенного интеграла.