Интегрирование по частям

Как следует из теоремы о дифференцировании произведения, интегрированием по частям называется нахождение интеграла по следующей формуле:

.

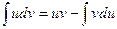Здесь 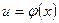, 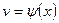- непрерывно дифференцируемые функции х. С помощью этой формулы нахождение интеграла 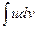сводится к отысканию другого интеграла 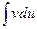. Ее применение целесообразно в том случае, когда последний интеграл либо проще исходного, либо подобен ему. При этом за и берется такая функция, которая при дифференцировании упрощается, а за dv – та часть подынтегрального выражения, интеграл от которой известен или может быть найден.

Отметим при этом, что для интегралов вида

, , ,

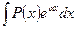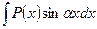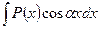где 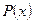- многочлен,

за и следует принять ,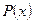

а за dv – соответственно выражения , , ;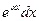

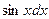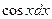для интегралов вида , , ,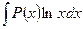

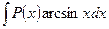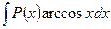за и принимают соответственно функции , , ,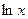

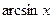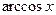а за dv – выражение .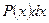

Пример 13.Найти интеграл .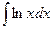

Положим 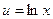, , 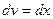тогда 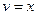, 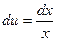. Используя формулу интегрирования по частям, получим

.

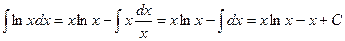Пример 14.Найти интеграл .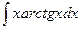

Пусть 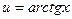, 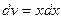; тогда 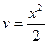, 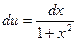. По формуле интегрирования по частям имеем

.

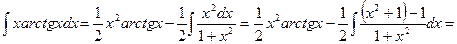
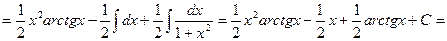
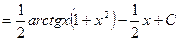Пример 15.Найти интеграл .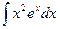

Положим 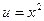, 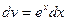; тогда 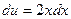, 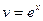.Применяем формулу интегрирования по частям:

.

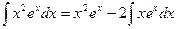Мы добились понижения степени х на единицу. Чтобы найти интеграл 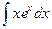, применим еще раз интегрирование по частям. Полагаем 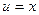, 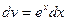; тогда 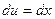, 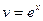. Окончательно получим

.

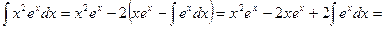
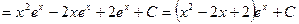Пример 16.Найти интеграл .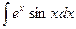

Пусть 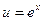, 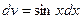; тогда 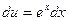, 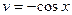. Следовательно,

.

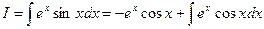Создается впечатление, что интегрирование по частям не привело к цели, поскольку интеграл не упростился. Попробуем, однако, еще раз проинтегрировать по частям. Приняв 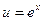, , 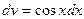откуда 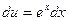, , 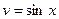получим

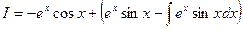
или

.

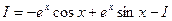Применив дважды операцию интегрирования по частям, мы в правой части получили исходный интеграл. Следовательно, приходим к уравнению с неизвестным интегралом I. Из этого уравнения находим

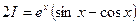, т.е. .

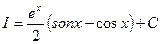В окончательном результате мы прибавили к найденной первообразной функции произвольную постоянную.