Или способом подстановки
Пусть требуется найти интеграл 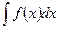 , причем непосредственно подобрать первообразную для
, причем непосредственно подобрать первообразную для 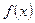 невозможно, но нам известно, что она существует. В данном случае можно осуществить замену переменной в неопределенном интеграле с помощью подстановок двух видов:
невозможно, но нам известно, что она существует. В данном случае можно осуществить замену переменной в неопределенном интеграле с помощью подстановок двух видов:
1) положим в подынтегральном выражении 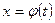 , где
, где 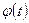 - монотонная, непрерывно дифференцируемая функция новой переменной t. Формула замены переменной в этом случае имеет вид
- монотонная, непрерывно дифференцируемая функция новой переменной t. Формула замены переменной в этом случае имеет вид
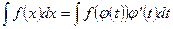 ;
;
2) если использовать подстановку вида 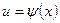 , где и – новая переменная, то формула замены переменной при ней будет
, где и – новая переменная, то формула замены переменной при ней будет
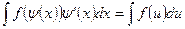 .
.
Пример 8.Найдем интеграл 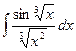 .
.
Произведем подстановку 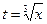 , т.е.
, т.е. 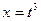 . Эта подстановка приведет к тому, что под знаком синуса окажется переменная интегрирования, а не корень из нее. Найдем дифференциал:
. Эта подстановка приведет к тому, что под знаком синуса окажется переменная интегрирования, а не корень из нее. Найдем дифференциал: 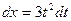 . Следовательно,
. Следовательно,
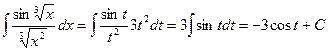 .
.
Ответ должен быть выражен через старую переменную х. Подставляя в результат интегрирования 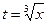 , получим
, получим
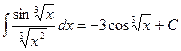 .
.
Пример 9.Найти интеграл 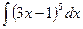 .
.
Полагая 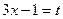 , имеем
, имеем 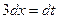 , т.е.
, т.е. 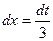 . Отсюда получим
. Отсюда получим
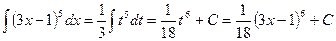 .
.
Пример 10.Найти интеграл 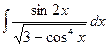 .
.
Произведем подстановку 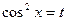 , тогда
, тогда 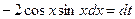 , т.е.
, т.е. 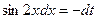 . Следовательно,
. Следовательно,
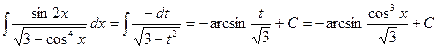 .
.
Пример 11.Найти интеграл 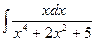 .
.
Преобразуем знаменатель дроби: 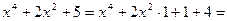
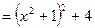 . Произведем подстановку
. Произведем подстановку 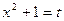 , тогда
, тогда 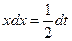 . Отсюда
. Отсюда
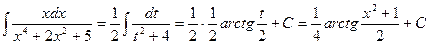 .
.
Пример 12.Найти интеграл 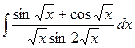 .
.
Полагая 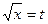 ,
, 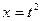 ,
, 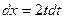 , получим
, получим
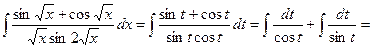
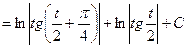 .
.
Возвращаясь к старой переменной, получим
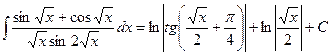 .
.
Дата добавления: 2021-01-26; просмотров: 395;











