Первообразная и неопределенный интеграл
В данном разделе мы будем рассматривать следующую задачу: дана функция 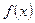 , требуется найти такую функцию
, требуется найти такую функцию 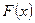 , производная которой равна
, производная которой равна 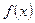 , т.е.
, т.е. 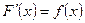 . С точки зрения механики это означает, что по известной скорости движения материальной точки, необходимо восстановить закон ее движения.
. С точки зрения механики это означает, что по известной скорости движения материальной точки, необходимо восстановить закон ее движения.
Определение.Функция 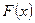 называется первообразной функции
называется первообразной функции 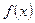 на интервале
на интервале 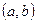 , если
, если 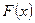 дифференцируема на
дифференцируема на 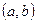 и
и 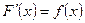 .
.
Подобным образом можно определить понятие первообразной и на отрезке 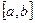 , но в точках a и b необходимо рассматривать односторонние производные.
, но в точках a и b необходимо рассматривать односторонние производные.
Пример 1. 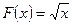 - есть первообразная для функции
- есть первообразная для функции 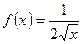 на
на 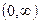 , так как
, так как 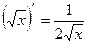 .
.
Пример 2. 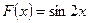 - есть первообразная для функции
- есть первообразная для функции 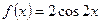 на
на 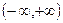 , так как
, так как 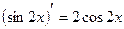 .
.
Отметим, что если функция 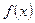 имеет первообразную
имеет первообразную 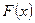 , то она имеет бесконечное множество первообразных, причем все первообразные содержатся в выражении
, то она имеет бесконечное множество первообразных, причем все первообразные содержатся в выражении 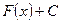 , где С – некоторая постоянная.
, где С – некоторая постоянная.
Определение. Неопределенным интегралом от функции 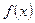 (или от выражения
(или от выражения 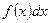 ) называется совокупность всех ее первообразных. Он обозначается следующим образом:
) называется совокупность всех ее первообразных. Он обозначается следующим образом:
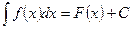 .
.
Здесь 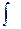 называется интегралом;
называется интегралом; 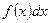 - подынтегральным выражением;
- подынтегральным выражением; 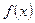 - подынтегральной функцией, а х – переменной интегрирования.
- подынтегральной функцией, а х – переменной интегрирования.
Таким образом, неопределенный интеграл представляет собой семейство функций 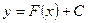 .
.
С геометрической точки зрения неопределенный интеграл представляет совокупность (семейство) кривых, каждая из которых получается путем сдвига одной из кривых параллельно самой себе вверх или вниз, т.е. вдоль оси Y.
Отметим далее, что если функция 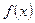 непрерывна на отрезке
непрерывна на отрезке 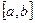 , то для этой функции существует первообразная (а следовательно, и неопределенный интеграл).
, то для этой функции существует первообразная (а следовательно, и неопределенный интеграл).
Нахождение первообразной для данной функции 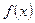 называется интегрированием функции
называется интегрированием функции 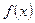 .
.
Приведем ряд свойств неопределенного интеграла, вытекающих из его определения:
1. 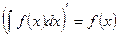 ;
;
2. 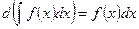 ;
;
3. 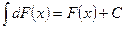 , где С – постоянная величина;
, где С – постоянная величина;
4. 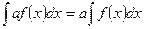 , где а – постоянная;
, где а – постоянная;
5. 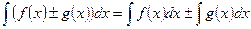 ;
;
6. Если 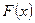 - есть первообразная для
- есть первообразная для 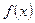 , то
, то
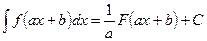 ;
;
7. Если 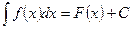 и
и 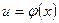 , то
, то 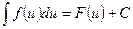 .
.
Прежде чем приступать к изучению методов интегрирования, приведем таблицу интегралов от простейших функций.
Таблица основных интегралов
I. 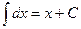 ,
,
II. 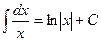 , x>0,
, x>0,
III. 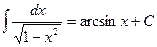 , |x|<1,
, |x|<1,
IV. 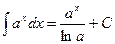 , a>0, a¹1,
, a>0, a¹1,
V. 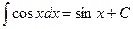 ,
,
VI. 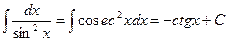 ,
,
VII. 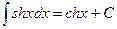 ,
,
VIII. 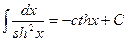 ,
,
IX. 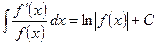 ,
,
X. 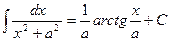 ,
,
XI. 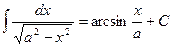 ,
,
XII. 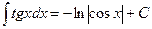 ,
,
XIII. 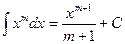 , при
, при 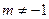 ,
,
XIV. 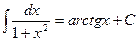 ,
,
XV. 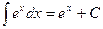 ,
,
XVI. 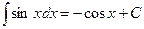 ,
,
XVII. 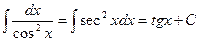 ,
,
XVIII. 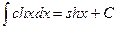 ,
,
XIX. 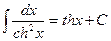 ,
,
XX. 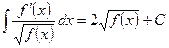 ,
,
XXI. 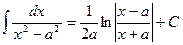 ,
,
XXII. 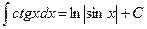 ,
,
XXIII. 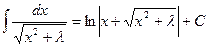 ,
,
XXIV. 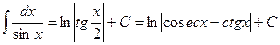 ,
,
XXV. 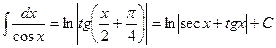 .
.
Приведем несколько примеров нахождения неопределенных интегралов, опираясь на их свойства и таблицу.
Пример 3.Найти интеграл 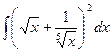 .
.
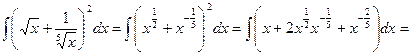
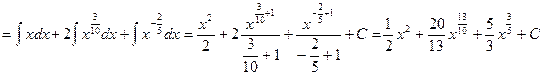 .
.
Пример 4.Найти интеграл 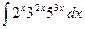 .
.
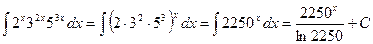 .
.
Заметим, что свойство 7 позволяет значительно расширить таблицу основных интегралов с помощью приема подведения функции под знак дифференциала (это, вообще говоря, замена переменной).
Пример 5. Найти интеграл 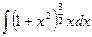 .
.
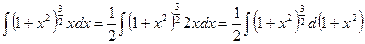 .
.
Теперь переменной интегрирования служит выражение 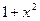 и относительно этой переменной получается интеграл от степенной функции. Следовательно,
и относительно этой переменной получается интеграл от степенной функции. Следовательно,
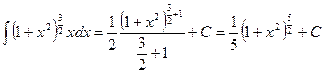 .
.
Пример 6.Найти интеграл 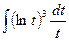 .
.
Выражение 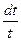 можно записать как
можно записать как 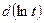 , поэтому
, поэтому
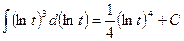 .
.
Пример 7.Найти интеграл 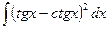 .
.
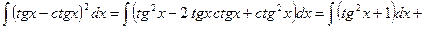
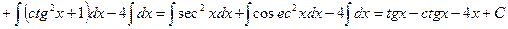 .
.
Дата добавления: 2021-01-26; просмотров: 409;











