Метод преобразования (свертки) схемы
Если схема электрической цепи содержит только один источник энергии (E или J), то пассивная часть схемы может быть преобразована (свернута) к одному эквивалентному элементу RЭ( рис. 7).
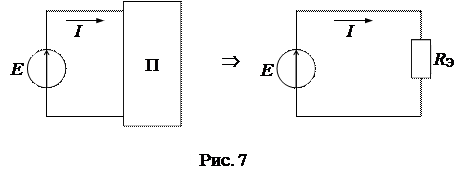 |
Свертка схемы начинается с самых удаленных от источника ветвей, проводится в несколько этапов до достижения полной свертки. После полной свертки схемы по закону Ома определяется ток источника: 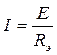 . Токи в остальных элементах исходной схемы находятся в процессе обратной развертки схемы. Такой метод расчета токов получил название метода последовательного преобразования (свертки) схемы.
. Токи в остальных элементах исходной схемы находятся в процессе обратной развертки схемы. Такой метод расчета токов получил название метода последовательного преобразования (свертки) схемы.
При применении данного метода возможны следующие виды преобразований.
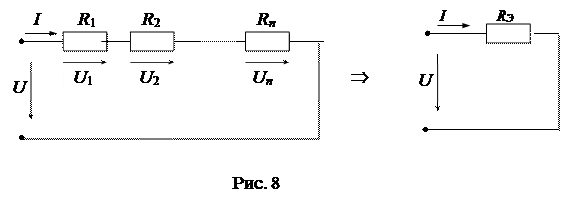
1) Последовательное преобразование заключается в замене нескольких элементов, включенных последовательно, одним эквивалентным (рис. 8).
Несложно доказать, что справедливы следующие соотношения:
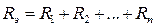 и
и 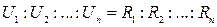
 |
2) Параллельное преобразование состоит в замене нескольких элементов, включенных параллельно, одним эквивалентным (рис. 9).
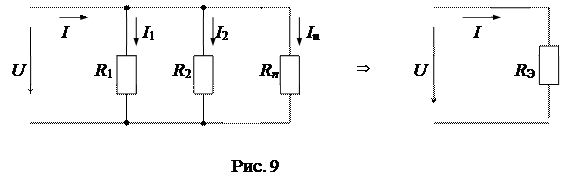 |
Несложно доказать, что справедливы следующие соотношения:
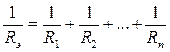 и
и 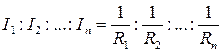
Для двух элементов: 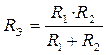 и
и 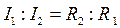
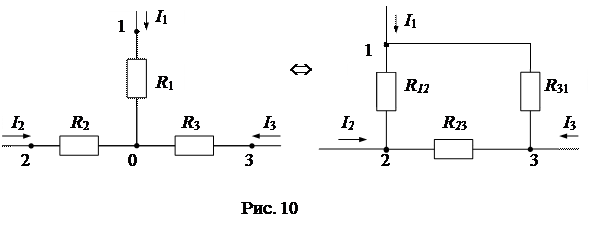
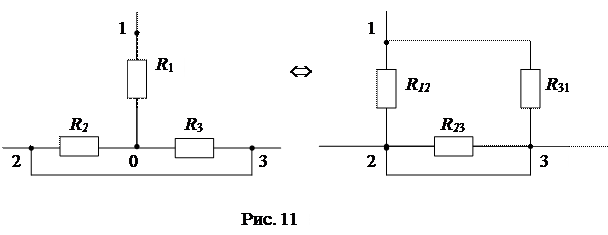
3) Взаимное преобразование схем звезда-треугольник (рис. 4) возникает при свертке сложных схем.
Условием эквивалентности двух схем являются равенства для них токов (I1, I2, I3), напряжений (U12, U23, U31) и входных сопротивлений (R12, R23, R31) и соответственно входных проводимостей ( G12, G23, G31).
Приравняем входные сопротивления для обеих схем со стороны двух произвольных ветвей при отключенной третей (рис. 10):
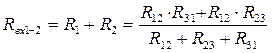 (1)
(1)
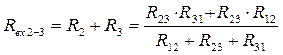 (2)
(2)
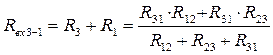 (3)
(3)
 |
Сложим почленно уравнения (1) и (3) и вычтем из суммы уравнение (2), получим:
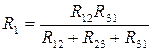 , по аналогии:
, по аналогии: 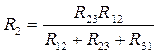 ,
, 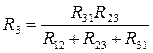 .
.
Приравняем входные проводимости для обеих схем со стороны произвольной вершины и двух других вершин, замкнутых накоротко (рис. 11):
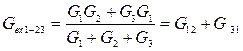 (4)
(4)
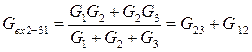 (5)
(5)
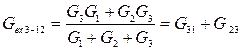 (6)
(6)
Сложим почленно уравнения (4) и (5) и вычтем уравнение (6), получим:
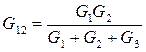 , по аналогии:
, по аналогии: 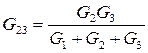 ,
, 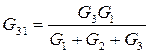 .
.
В последних уравнениях заменим проводимости на соответствующие им сопротивления 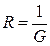 , получим:
, получим:
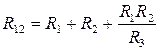 ;
; 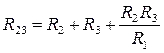 ;
; 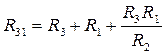 .
.
При наличии полной симметрии соотношение между параметрами эквивалентных схем составляет: 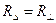 .
.
4) Замена параллельных ветвей эквивалентной ветвью (рис. 12) осуществляется согласно теореме об эквивалентном генераторе.
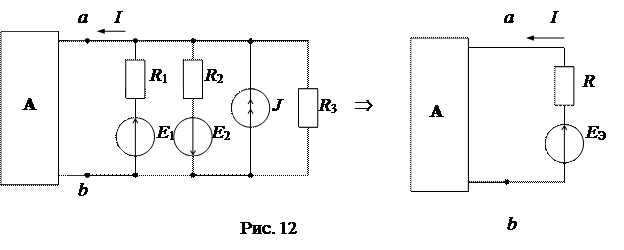 |
Напряжение холостого хода Uxxaв=EЭ определяется по методу двух узлов:
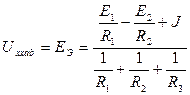 .
.
Эквивалентное входное сопротивление находится методом свертки схемы:
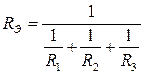 .
.
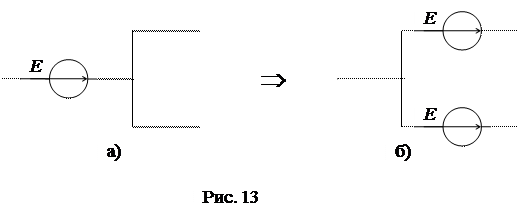
5) Перенос источника ЭДС через узел схемы: источник ЭДС Е можно перенести через узел во все ветви, отходящие от узла (рис. 13а, б.).
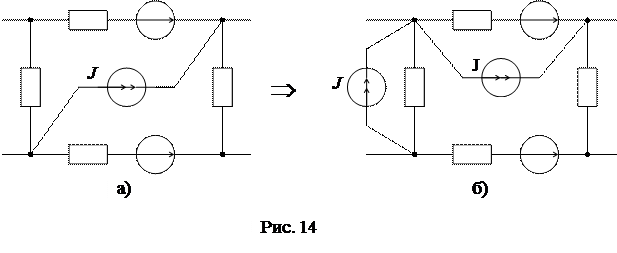
6) Привязка источника токак произвольному узлу согласно схеме(рис. 14а, б):
 |
7) Взаимное преобразование схемс источником напряжения и систочником тока согласно схеме(рис. 15а, б):
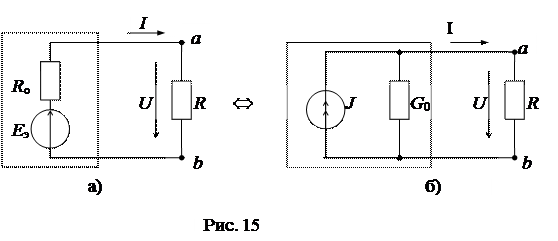 |
Схемы эквивалентны при равенстве для обеих напряжений U и токов I на нагрузке:
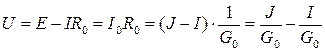 .
.
Сравнивая левые и правые части равенства, получим соотношения между параметрами эквивалентных схем:
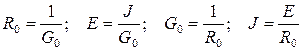 .
.
Дата добавления: 2016-10-18; просмотров: 2974;











