Свойства математических моделей

Из сказанного ранее следует, что при изучении реально существующей или гипотетической системы математические методы применяют к ее математической мо­дели. Это применение будет эффективным, если свойства ММ удовлетворяют определенным требованиям. Рассмотрим эти свойства.

Полнота ММ позволяет отразить в достаточной мере именно те характеристики и особенности системы, которые интересуют нас с точки зрения поставленной цели проведения вычислительного эксперимента. Например, модель может до­статочно полно описывать протекающие в системе процессы, но не отражать его габаритные, массовые или стоимостные показатели.

Точность ММдает возможность обеспечить приемлемое совпадение реальных и найденных при помощи ММ значений выходных параметров системы, составляющих вектор

.

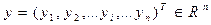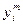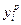Пусть и — найденное при помощи ММ и реальное значения i-гo выходного параметра. Тогда относительная погрешность ММ по отношению к этому параметру будет равна

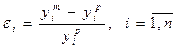
В качестве скалярной оценки вектора

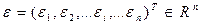
можно принять какую-либо его норму, например

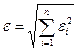или .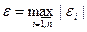

Поскольку выходные параметры системы при помощи ММ связаны с его внешними и внутренними параметрами, то 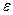, как количественная характеристика точности модели этой системы, будет зависеть от их значений. Адекватность ММ— это способность ММ отражать свойства системы с относительной погрешностью не хуже заданной.

В общем смысле под адекватностью ММ понимают правильное качественное и достаточно точное количественное описание именно тех характеристик системы, которые важны в дан­ном конкретном случае. Модель, адекватная при выборе одних характеристик, может быть неадекватной при выборе других характеристик системы. В ряде прикладных областей, еще недостаточно подготовленных к применению количественных математических методов, ММ имеют главным образом каче­ственный характер. Эта ситуация типична, например, для биологической и социальной сфер, в которых количественные закономерности не всегда поддаются строгой математической формализации. В таких случаях под адекватностью ММ есте­ственно понимать лишь правильное качественное описание поведения изучаемых систем.

Экономичность ММоценивают затратами на вычисли­тельные ресурсы (машинное время и память), необходимые для реализации ММ на ЭВМ. Эти затраты зависят от числа арифметических операций при использовании модели, от раз­мерности пространства фазовых переменных, от особенностей применяемой ЭВМ и других факторов. Очевидно, что требова­ния экономичности, высокой точности и достаточно широкой области адекватности ММ противоречивы и на практике могут быть удовлетворены лишь на основе разумного компромисса. Свойство экономичности ММ часто связывают с ее простотой. Более того, количественный анализ некоторых упрощенных вариантов ММ может быть осуществлен и без привлечения со­временной вычислительной техники. Однако его результаты могут иметь лишь ограниченную ценность на стадии отладки алгоритма или программы, если упро­щение ММ не согласовано с концептуальной моделью системы.

Робастность ММхарактеризует ее устойчивость по отноше­нию к погрешностям исходных данных, способность нивели­ровать эти погрешности и не допускать их чрезмерного влия­ния на результат вычислительного эксперимента. Причинами низкой робастности ММ могут быть необходимость при ее количественном анализе вычитания близких друг к другу при­ближенных значений величин или деления на малую по модулю величину, а также использование в ММ функций, быстро из­меняющихся в промежутке, где значение аргумента известно с невысокой точностью.

Продуктивность ММсвязана с достоверностью исходных данных. Если они являются результатом измерений, то точность их измерения должна быть выше, чем для тех параметров, которые получа­ются при использовании ММ. В противном случае ММ будет непродуктивной и ее применение для анализа конкретной системы потеряет смысл. Ее можно будет использовать лишь для оценки и характеристик некоторого класса систем с гипотетическими исходными данными.

Наглядность ММ является желательным, но необязательным свойством. Однако использование ММ и ее модификация упрощаются, если ее составляющие (например, отдельные члены уравнений) имеют ясный содержательный смысл. Это позволяет предвидеть результаты вычислительного эксперимента и облегчить контроль их правильности.