Модель сложной системы

Для рассмотрения понятия математической модели необходимо ввести обозначения: временной интервал моделирования системы (интервал модельного времени) – T_x=[t₀, T],

где t₀ - время начала моделирования, обычно полагают t_o = 0, Т– время окончания моделирования; 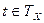– текущее значение модельного времени.

Параметры системы β₁, β₂, β_3,… β_m – характеристики системы, остающиеся постоянными на всем интервале моделирования .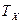

Множество переменных системы разбивают на два подмножества – зависимых и независимых переменных.

К независимым переменным отнесем следующие характеристики.

Входные воздействия на систему (сигналы): 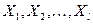Входные воздействия в момент 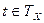характеризуются вектором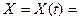

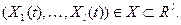
Среди 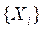могут быть управляющие воздействия, например,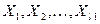 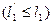, а остальные 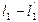воздействий – не управляющие.

Воздействия внешней среды. Среди них могут быть контролируемые (наблюдаемые) и неконтролируемые (ненаблюдаемые), детерминированные и случайные воздействия. В момент 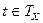они характеризуются вектором

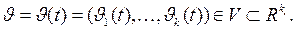
В качестве примера приведем наличие дефектов у заготовок для деталей: внешние дефекты – контролируемые, а внутренние (скрытые) – неконтролируемые воздействия; случайные интервалы времени между поступлением деталей на обработку.

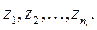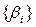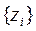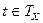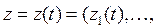
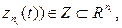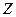Переменные, характеризующие состояние системы: В отличие от состояния характеризуют свойства системы, изменяющиеся во времени. Состояние системы в момент описывается вектором где – пространство состояний или фазовое пространство системы (множество возможных значений вектора ).

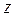Если моменты изменения состояния системы 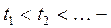, то последовательность 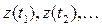называется фазовой траекторией системы.

Начальное состояние системы характеризуют вектором 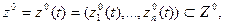Z⁰ - пространство начальных состояний.

К зависимым переменным относят выходные характеристики системы 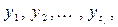определяемые в момент 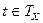вектором

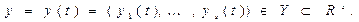
Изобразим связи между зависимыми и независимыми переменными (рис. 2.3).

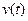
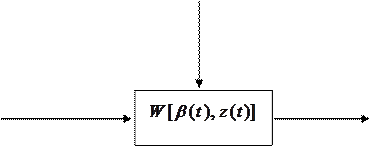
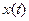
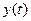
Рис. 2.3 Связь между зависимыми и независимыми переменными системы

Реальную сложную систему можно характеризовать набором свойств, которые соответствуют целям ее применения и могут быть измерены или вычислены.

Пусть m – свойств системы являются независимыми и могут изменяться в некоторых пределах. Выбор характеристик m, n, s, определяется задачами исследования. Если параметры, входные воздействия и воздействия внешней среды играют роль независимых переменных, то математическое описание представляется соотношениями (2.1) или в векторной форме (2.2).

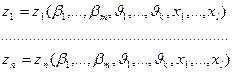
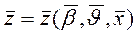
(2.1) (2.2)

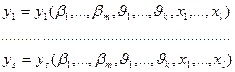
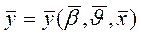
Такое математическое описание представляет собой структурную идентификацию сложной системы.

Зависимости (2.1), (2.2) называются законами функционирования системы. Зависимость 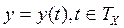называется выходной траекторией системы. Зависимость 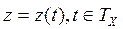называется фазовой траекториейсистемы.

Таким образом, математической моделью системы называется множество переменных 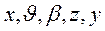вместе с законом функционирования в виде (2.1), (2.2).

Для каждой исследуемой системы можно построить несколько математических моделей в зависимости от цели исследования. Общее требование к модели состоит в том, что она должна быть адекватной реальной системе, т.е. математическое описание должно отражать с заданной точностью существенные свойства системы.