Типовые математические схемы моделирования

Модель сложной системы, рассмотренная ранее, представляет собой математическую схему моделирования общего вида. На практике для формализации концептуальных моделей ряда систем выгоднее применять типовые математические схемы моделирования, учитывающие с одной стороны способ представления времени в модели (непрерывная переменная или дискретная), а с другой стороны степень случайности моделируемых процессов. По этим признакам различают следующие математические схемы моделирования (классы ММ).

Непрерывно – детерминированные модели (D – схемы).

Дискретно – детерминированные модели (F – схемы).

Дискретно – вероятностные модели (P – схемы).

Непрерывно - вероятностные модели (Q – схемы).

Сетевые модели (N – схемы).

Агрегатные модели (А – схемы).

Непрерывно-детерминированные модели. В этих моделях время t полагается непрерывной переменной, а случайными факторами в системе пренебрегают. Математический аппарат моделей – теория дифференциальных и интегральных уравнений, с помощью которой достигается адекватное описание динамических систем. Наиболее глубоко разработан операторный метод описания и исследования процессов функционирования динамических систем и их структур.

Примером непрерывно – детерминированной модели одноканальной системы автоматического управления является неоднородное дифференциальное уравнение с постоянными коэффициентами.

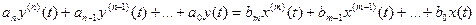. (2.5)

В этом уравнении x(t)- входное воздействие; y(t) – выходная величина, характеризующая положение объекта управления; 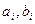- внутренние параметры системы.

Если динамическая система описывается нелинейным дифференциальным уравнением, то его линеаризуют и решают как линейное.

Применение непрерывно – детерминированных моделей позволяет количественно осуществлять не только анализ динамических систем, но и оптимальный синтез их.

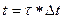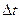Дискретно-детерминированные модели. В дискретно–детерминированных (ДД) моделях время t является дискретной переменной , где – шаг дискретизации, а 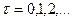– дискретные моменты времени.

Основной математический аппарат, используемый при построении ДД – моделей – это теория разностных уравнений и аппарат дискретной математики, в частности, теория конечных автоматов.

Разностное уравнение – это уравнение, содержащее конечные разности искомой функции

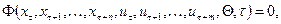(2.6)

где 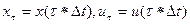– соответственно состояние системы и внешнее воздействие в дискретные моменты времени .

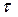В прикладных задачах ДД – модели в виде (2.6) часто возникают как промежуточные при исследовании НД – моделей на ЭВМ, когда аналитическое решение дифференциального уравнения получить не удается и приходится применять разностные схемы.

Кратко рассмотрим теорию конечных автоматов, которая используется для построения ДД – моделей.

Конечный автомат – это математическая модель дискретной системы, которая под действием входных сигналов 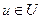вырабатывает выходные сигналы 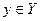, и которая может иметь некоторые изменяемые внутренние состояния 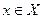; здесь 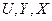– конечные множества.

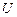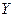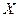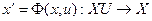Конечный автомат характеризуется: входным алфавитом ; выходным алфавитом ; внутренним алфавитом состояний ; начальным состоянием ; функцией переходов ; функцией выходов .

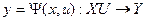Процесс функционирования конечного автомата таков. В 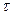–м такте 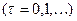на вход автомата, находящегося в состоянии 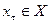, поступает входной сигнал 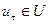, на который автомат реагирует переходом на 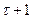–м такте в состояние 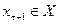и выдачей выходного сигнала 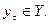Например, конечный автомат Мили описывается следующими рекуррентными соотношениями:

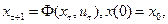(2.7)

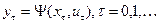
Дискретно–вероятностные модели. В дискретно–вероятностной модели учитываются случайные элементы исследуемой сложной системы. Основной математический аппарат, используемый при построении и исследовании ДВ – моделей, – это теория разностных стохастических уравнений и теория вероятностных автоматов.

Разностное стохастическое уравнение – это такое уравнение, которое содержит случайные параметры 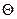или случайные входные воздействия .

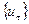Пусть на вероятностном пространстве 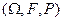определен случайный 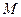– вектор параметров 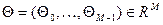и случайная последовательность входных воздействий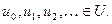

Нелинейное разностное стохастическое уравнение порядка 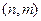имеет вид 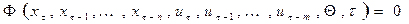, (2.8)

где 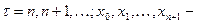заданные начальные состояния системы; 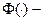заданная функция 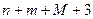переменных.

Решением этого уравнения является определенная на множестве 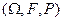случайная последовательность состояний моделируемой системы:

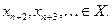
Если функция 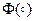линейная по 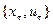, то (2.8) примет вид:

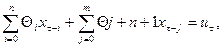
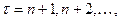(2.9)

где 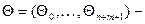вектор 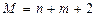параметров.

Другой математический аппарат построения ДВ – моделей сложных систем представляет теория вероятностных автоматов.

Вероятностный автомат, определенный на множестве 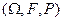, есть конечный автомат, в котором функция переходов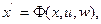 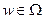и функция выходов 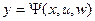являются случайными функциями, имеющими некоторые вероятностные распределения.

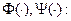
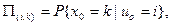
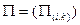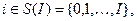
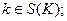
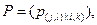
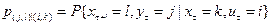
Примем обозначения для вероятностных распределений – начальное распределение вероятностей, 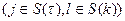– вероятность события, состоящего в том, что находящийся в 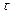–м такте в состоянии 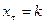автомат под воздействием входного сигнала 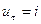выдаст выходной сигнал 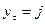и перейдет на 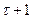–м такте в состояние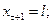

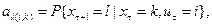
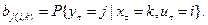
Математическая модель вероятностного автомата полностью определяется пятью элементами: .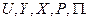

Непрерывно – вероятностные модели. При построении и исследовании НВ – моделей используется теория стохастических дифференциальных уравнений и теория массового обслуживания.

Стохастическое дифференциальное уравнение (в форме Ито) имеет вид:

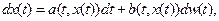
где 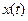– случайный процесс, определяющий состояние системы в момент времени 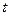; 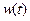– стандартный винеровский случайный процесс; 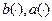– коэффициенты диффузии и переноса. НВ – модель часто используется при моделировании стохастических систем управления, процессов обмена.

Теория массового обслуживания разрабатывает и исследует математические модели различных по своей природе процессов функционирования систем, например: поставок сырья и комплектующих изделий некоторому предприятию; заданий, поступающих на ЭВМ от удаленных терминалов; вызов на телефонных станциях и т.д. Для функционирования таких систем характерна стохастичность: случайность моментов времени появления заявок на обслуживание и т.д.

Система, описываемая как система массового обслуживания (СМО), состоит из 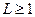приборов обслуживания 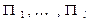. Прибор обслуживания 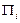состоит из накопителя заявок 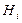, в котором могут одновременно находиться 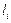заявок 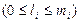, и канала 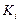обслуживания заявок; 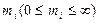– емкость накопителя 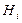, то есть число мест в очереди на обслуживание заявок в канале .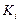

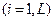На каждый элемент прибора 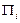поступают потоки событий; в накопитель 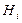– поток заявок 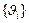, на канал 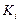– поток «обслуживаний» 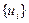. Поток заявок 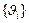представляет последовательность интервалов времени между моментами появления заявок на входе СМО и образует подмножество неуправляемых переменных СМО. А поток 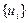представляет собой последовательность интервалов времени между моментами начала и окончания обслуживания заявок и образует подмножество управляемых переменных.

Заявки, обслуженные СМО, образуют выходной поток 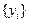– последовательность интервалов времени между моментами выхода заявок. Не обслуженные заявки, но покинувшие СМО по различным причинам, образуют выходной поток потерянных заявок.

Сетевые модели используют для формализации причинно – следственных связей в сложных системах с параллельными процессами. В основе этих моделей лежит сеть Петри. При графической интерпретации сеть Петри представляет собой граф особого вида, состоящий из вершин двух типов – позиций и переходов, соединенных ориентированными дугами, причем каждая дуга может связывать лишь разнотипные вершины (позицию с переходом или переход с позицией). Вершины-позиции обозначаются кружками, вершины-переходы – черточками. С содержательной точки зрения переходы соответствуют событиям, присущим исследуемой системе, а позиции – условиям их возникновения.

Таким образом, совокупность переходов, позиций и дуг позволяет описать причинно-следственные связи, присущие системе, но в статике. Чтобы сеть Петри «ожила», вводят еще один вид объектов сети – так называемые фишки или метки позиций, которые перемещаются по переходам сети при условии наличия метки во входной позиции и отсутствии метки в выходной позиции. Расположение фишек в позициях сети называется разметкой сети.

Агрегатные модели. Анализ существующих задач приводит к выводу о том, что комплексное решение проблем возможно лишь в том случае, если моделирующие системы имеют в своей основе единую математическую схему моделирования. Такой подход к формализации процесса функционирования сложной системы предложен Бусленко Н.П. [1] и базируется на понятии «агрегата».

При агрегатном описании сложная система разбивается по подсистемы, сохраняя при этом связи обеспечивающие взаимодействие их. Если подсистема оказывается сложной, то процесс расчленения продолжается до тех пор, пока не образуются подсистемы, которые в условиях рассматриваемой задачи могут считаться удобными для математического описания.

В результате этого получается многоуровневая конструкция из взаимосвязанных элементов объединенных в подсистемы различных уровней. Элементами агрегатной модели являются агрегаты. Связи между агрегатами и внешней средой осуществляются с помощью операторов сопряжения. Сам агрегат тоже может рассматриваться как агрегатная модель, то есть разбиваться на элементы следующего уровня.

Любой агрегат характеризуется множествами: моментов времени T, входных X и выходных Y сигналов, состояний агрегата Z в каждый момент времени t. Процесс функционирования агрегата состоит из скачков состояний 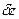в моменты поступлений входных сигналов x и изменений состояний между этими моментам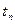и и .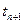

Моменты скачков 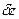, не являющиеся моментами поступления входных сигналов называют особыми моментами времени 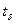, а состояния 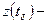особыми состояниями агрегатной схемы. В множестве состояний Z выделяют подмножество 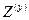, что если 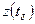достигает 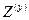, то это состояние является моментом выдачи выходного сигнала y.