Математические ожидания функций дискретных случайных переменных
Пусть 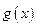 – некоторая функция от x. Тогда
– некоторая функция от x. Тогда 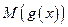 – математическое ожидание
– математическое ожидание 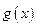 записывается как
записывается как
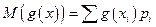 , (3)
, (3)
где суммирование производится по всем возможным значениям x. В табл. 3 показана последовательность практического расчета математического ожидания функции от x.
Таблица 3
| x | Вероятность | Функция от x | Функция, взвешенная по вероятности |
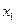
| 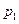
| 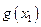
| 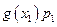
|
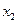
| 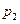
| 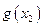
| 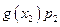
|
| … | … | … | … |
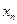
| 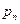
| 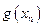
| 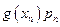
|
| Всего | 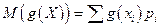
|
Предположим, что x может принимать n различных значений от 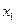 до
до 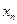 с соответствующими вероятностями от
с соответствующими вероятностями от 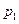 до
до 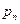 . В первой колонке записываются все возможные значения x. Во второй – записываются соответствующие вероятности. В третьей колонке рассчитываются значения функции для соответствующих величин x. В четвертой колонке перемножаются числа из колонок 2 и 3. Ответ приводится в суммирующей строке колонки 4.
. В первой колонке записываются все возможные значения x. Во второй – записываются соответствующие вероятности. В третьей колонке рассчитываются значения функции для соответствующих величин x. В четвертой колонке перемножаются числа из колонок 2 и 3. Ответ приводится в суммирующей строке колонки 4.
Рассчитаем математическое ожидание величины 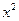 . Для этого рассмотрим пример с числами, выпадающими при бросании одной кости. Использовав схему, приведенную в табл. 3, заполним табл. 4.
. Для этого рассмотрим пример с числами, выпадающими при бросании одной кости. Использовав схему, приведенную в табл. 3, заполним табл. 4.
Таблица 4
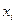
| 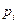
| 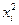
| 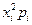
|
| 1/6 | 0,167 | ||
| 1/6 | 0,667 | ||
| 1/6 | 1,500 | ||
| 1/6 | 2,667 | ||
| 1/6 | 4,167 | ||
| 1/6 | 6,000 | ||
| Всего | 15,167 |
В четвертой ее колонке даны шесть значений 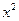 , взвешенных по соответствующим вероятностям, которые в данном примере все равняются 1/6. По определению, величина
, взвешенных по соответствующим вероятностям, которые в данном примере все равняются 1/6. По определению, величина 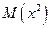 равна
равна 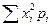 , она приведена как сумма в четвертой колонке и равна 15,167.
, она приведена как сумма в четвертой колонке и равна 15,167.
Математическое ожидание x, как уже было показано, равно 3,5, и 3,5 в квадрате равно 12,25. Таким образом, величина 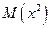 не равна
не равна 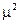 , и, следовательно, нужно аккуратно проводить различия между
, и, следовательно, нужно аккуратно проводить различия между 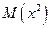 и
и 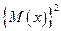 .
.
Дата добавления: 2016-10-18; просмотров: 1421;











