Теоретическая дисперсия дискретной случайной переменной

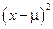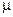Теоретическая дисперсия является мерой разброса для вероятностного распределения. Она определяется как математическое ожидание квадрата разности между величиной x и ее средним, т.е. величины , где – математическое ожидание x. Дисперсия обычно обозначается как 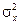или 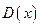, и если ясно, о какой переменной идет речь, то нижний индекс может быть опущен:

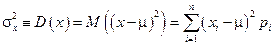. (8)

Из 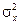можно получить 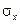– среднее квадратическое отклонение – столь же распространенную меру разброса для распределения вероятностей; среднее квадратическое отклонение случайной переменной есть квадратный корень из ее дисперсии.

Проиллюстрируем расчет дисперсии на примере с одной игральной костью. Поскольку 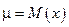, то 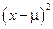в этом случае равно 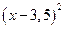. Мы рассчитаем математическое ожидание величины 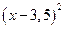, используя схему, представленную в табл. 5. Дополнительный столбец 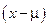представляет определенный этап расчета 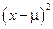. Суммируя последний столбец в табл. 5, получим значение дисперсии 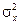, равное 2,92. Следовательно, стандартное отклонение ( 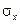) равно 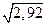, то есть 1,71.

Таблица 5

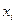
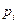
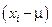
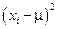
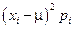
	1/6	–2,5	6,25	1,042
	1/6	–1,5	2,25	0,375
	1/6	–0,5	0,25	0,042
	1/6	0,5	0,25	0,042
	1/6	1,5	2,25	0,375
	1/6	2,5	6,25	1,042
Всего	2,92

Одним из важных приложений правил расчета математического ожидания является формула расчета теоретической дисперсии случайной переменной, которая может быть записана как

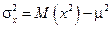. (9)

Это выражение иногда оказывается более удобным, чем первоначальное определение.