Постоянная и случайная составляющие случайной переменной
Часто вместо рассмотрения случайной величины как единого целого можно и удобно разбить ее на постоянную и чисто случайную составляющие, где постоянная составляющая всегда есть ее математическое ожидание. Если x – случайная переменная и 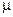 – ее математическое ожидание, то декомпозиция случайной величины записывается следующим образом:
– ее математическое ожидание, то декомпозиция случайной величины записывается следующим образом:
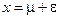 , (14)
, (14)
где 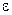 – чисто случайная составляющая.
– чисто случайная составляющая.
Из формулы (14) следует, что случайная составляющая 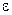 определяется как разность между x и
определяется как разность между x и 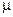
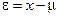 . (15)
. (15)
Из определения следует, что математическое ожидание величины 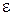 равно нулю:
равно нулю:
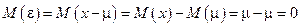 .
.
Поскольку весь разброс значений 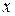 обусловлен
обусловлен 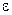 , следовательно, и теоретическая дисперсия
, следовательно, и теоретическая дисперсия 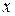 равна теоретической дисперсии
равна теоретической дисперсии 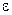 . Последнее нетрудно доказать. По определению,
. Последнее нетрудно доказать. По определению,
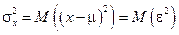
и
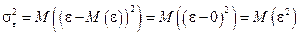 .
.
Таким образом, 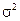 может быть эквивалентно определена как дисперсия x или
может быть эквивалентно определена как дисперсия x или 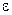 .
.
Обобщая, можно утверждать, что если x – случайная переменная, определенная по формуле (14), где 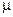 – заданное число и
– заданное число и 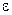 – случайный член с
– случайный член с 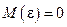 и
и 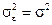 , то математическое ожидание величины x равно
, то математическое ожидание величины x равно 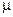 , а дисперсия –
, а дисперсия – 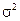 .
.
Дата добавления: 2016-10-18; просмотров: 1668;











