Минимальное время регулирования
Цифровой способ управления дает возможность создать регуляторы, обеспечивающие завершение переходного процесса в контуре регулирования за конечное число периодов дискретности [13]. Несмотря на некоторые недостатки такого рода систем регулирования, связанные с возможностью их реализации только для одного вида управляющего воздействия (ступенчатого, линейного и пр.), они получили определенное распространение.
Введем следующие обозначения: 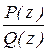 – ДПФ неизменяемой части системы регулирования,
– ДПФ неизменяемой части системы регулирования, 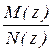 – ДПФ последовательного цифрового фильтра – регулятора скорости.
– ДПФ последовательного цифрового фильтра – регулятора скорости.
ДПФ разомкнутой системы регулирования 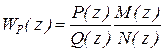 , а соответствующая ДПФ замкнутой системы с единичной отрицательной обратной связью
, а соответствующая ДПФ замкнутой системы с единичной отрицательной обратной связью
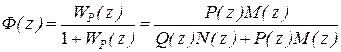 . (5.25)
. (5.25)
ДПФ неизменяемой части системы представим в виде
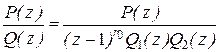 , (5.26)
, (5.26)
где Q1(z) – полином, содержащий все левые нули Q(p), Q2(z) – полином, содержащий все правые нули Q(p), ro – порядок астатизма объекта регулирования (неизменяемой части системы).
Для устойчивых объектов регулирования Q2(z) всегда отсутствует. При последовательной коррекции Q1(z) должна быть скомпенсирована ДПФ регулятора, кроме того, системе регулирования скорости необходимо придать астатизм порядка ‘r’. С учетом этого ДПФ разомкнутой системы должна быть равна
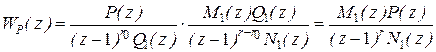 , (5.27)
, (5.27)
где 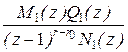 – ДПФ регулятора скорости.
– ДПФ регулятора скорости.
Желаемая ДПФ замкнутой системы, переходной процесс в которой заканчивается за конечное и минимальное время равна [7]:
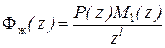 , (5.28)
, (5.28)
где 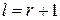 определяет минимальное число периодов дискретности для достижения установившегося состояния.
определяет минимальное число периодов дискретности для достижения установившегося состояния.
Для нахождения неизвестных полиномов M1(z) и N1(z) воспользуемся равенством знаменателей желаемой и исходной ДПФ разомкнутой системы
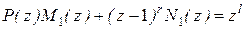 . (5.29)
. (5.29)
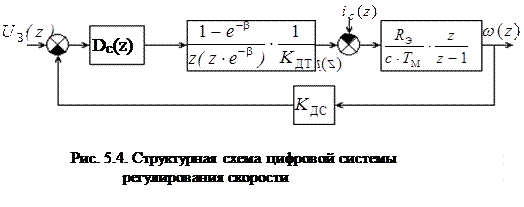 |
При определении полиномов P(z), Q(z) и
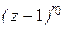 неизменяемой части системы для подчиненной системы регулирования учтем, что в ее состав входит замкнутый контур регулирования тока. Структурная схема системы регулирования скорости в дискретной форме представлена на рис. 5.4.
неизменяемой части системы для подчиненной системы регулирования учтем, что в ее состав входит замкнутый контур регулирования тока. Структурная схема системы регулирования скорости в дискретной форме представлена на рис. 5.4.
Звено с ДПФ 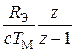 изображает электромеханическую часть электропривода. Эта ДПФ получается в результате z – преобразования передаточной функции электромеханической части ДПТ
изображает электромеханическую часть электропривода. Эта ДПФ получается в результате z – преобразования передаточной функции электромеханической части ДПТ
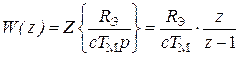 . (5.30)
. (5.30)
Таким образом, ДПФ неизменяемой части системы регулирования скорости с учетом замкнутого контура тока равна:
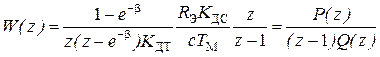 , (5.31)
, (5.31)
где 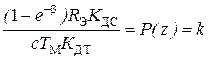 ,
, 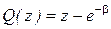 ,
, 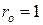 .
.
Выполним синтез регулятора скорости для астатизма регулятора 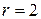 . Величина
. Величина 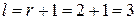 , обеспечивает минимальное время переходного процесса. Находим порядок полиномов
, обеспечивает минимальное время переходного процесса. Находим порядок полиномов 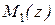 и
и 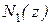 :
: 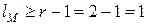 ,
, 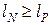 ,
, 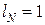 . Следовательно,
. Следовательно, 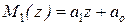 ,
, 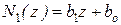 , а из равенства
, а из равенства 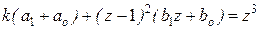 находим неизвестное а1, а0, b1 и b0. Для этого приравняем коэффициенты левой и правой частей при различных степенях z:
находим неизвестное а1, а0, b1 и b0. Для этого приравняем коэффициенты левой и правой частей при различных степенях z:
z3 : 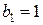 ,
,
z2 : 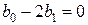 ,
,
z1 : 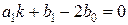 ,
,
z0 : 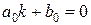
откуда 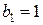 ,
, 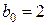 ,
, 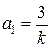 ,
, 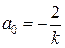 , т.е.
, т.е. 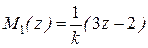 ,
, 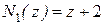 .
.
В результате ДПФ регулятора скорости 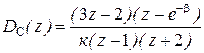 , а ДПФ разомкнутой системы равна
, а ДПФ разомкнутой системы равна 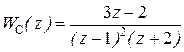 и ДПФ замкнутой системы примет вид
и ДПФ замкнутой системы примет вид 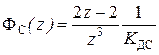 .
.
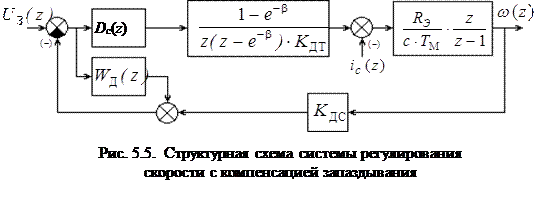 |
При необходимости можно рассмотренным выше способом ввести импульсную коррекцию запаздывания на один период дискретности, например, при использовании датчиков скорости с усреднением за период дискретности. Результаты расчетов регулятора скорости и корректирующих фильтров, выполненных в соответствии с рис.5.5, приведены в табл. 5.2.
Анализ переходных процессов в САР скорости показывает, что обеспечение конечной длительности переходных процессов не всегда сопровождается соблюдением его высокого качества, так при 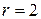 перерегулирование может достигать 100%. Снижение перерегулирования достигается введением “коэффициента жесткости” – х [6]. В табл.2 приводятся данные по полиномам
перерегулирование может достигать 100%. Снижение перерегулирования достигается введением “коэффициента жесткости” – х [6]. В табл.2 приводятся данные по полиномам 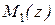 и
и 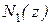 , выбранным с учетом коэффициента жесткости из выражения
, выбранным с учетом коэффициента жесткости из выражения
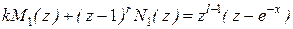 . (5.32)
. (5.32)
Рассмотрим синтез регулятора скорости и компенсирующего запаздывание корректирующего устройства для системы с ДПФ неизменяемой части системы
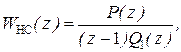
где 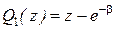 ,
, 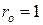 , а
, а 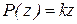 , что необходимо для компенсации запаздывания. Рассмотрим случай, когда
, что необходимо для компенсации запаздывания. Рассмотрим случай, когда 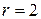 , порядки полиномов
, порядки полиномов 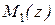 и
и 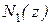 равны
равны 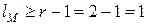 ,
, 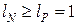 , следовательно,
, следовательно, 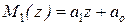 ;
; 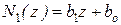 . Определим
. Определим 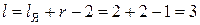 .
.
Из условия 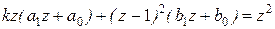 найдем а1, а0, b1 и b0, приравняв коэффициенты при соответствующих степенях z:
найдем а1, а0, b1 и b0, приравняв коэффициенты при соответствующих степенях z:
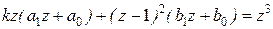
z3 : 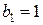 ,
,
z2 : 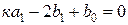 ,
,
z1 : 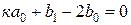 ,
,
z0 : 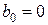 ,
,
находим 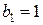 ,
, 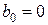 ,
, 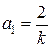 ,
, 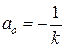 .
.
Затем находим 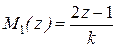 ,
, 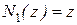 . Таким образом, ДПФ регулятора скорости равна
. Таким образом, ДПФ регулятора скорости равна 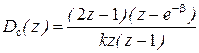 . ДПФ разомкнутой системы
. ДПФ разомкнутой системы
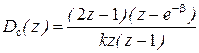 . (5.33)
. (5.33)
ДПФ корректирующего фильтра запаздывания
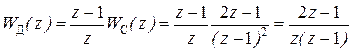 . (5.34)
. (5.34)
Рассмотрим случай, когда с целью уменьшения перерегулирования вводится “коэффициент жесткости”. Одновременно с этим введем условие компенсации запаздывания на один такт. Рассмотрим синтез регулятора для 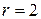 и для неизменяемой части системы, когда
и для неизменяемой части системы, когда
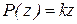 ,
, 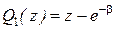 ,
, 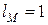 ,
, 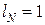 и
и 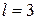 .
.
Находим коэффициенты полиномов 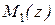 и
и 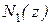 из условия
из условия
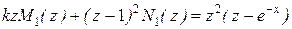 , (5.35)
, (5.35)
или 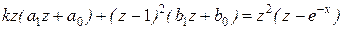 .
.
Приравнивая коэффициенты левой и правой частей равенства при одинаковых степенях z
z3 : 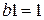
z2 : 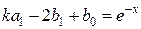
z1 : 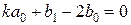
z0 : 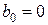 ,
,
находим коэффициенты 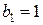 ,
, 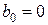 ,
, 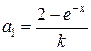 ;
; 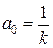 . Следовательно, полиномы равны
. Следовательно, полиномы равны 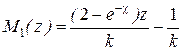 ,
, 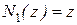 , а ДПФ регулятора скорости
, а ДПФ регулятора скорости 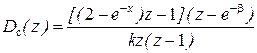 . ДПФ корректирующего запаздывание фильтра
. ДПФ корректирующего запаздывание фильтра 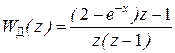 , а ДПФ замкнутой системы регулирования скорости
, а ДПФ замкнутой системы регулирования скорости 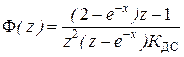 .
.
Пример расчета 9. Рассчитаем регулятор скорости и корректирующий запаздывание на один такт фильтр для условий и результатов расчета регулятора тока в примере расчета 5. ДПФ замкнутого контура регулирования тока
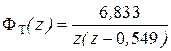
ДПФ неизменяемой системы в контуре регулирования скорости
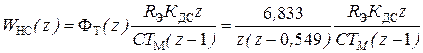 .
.
С учетом того, что 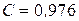
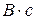 ,
, 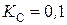
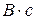 ,
, 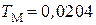 с и
с и 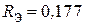 Ом, находим
Ом, находим
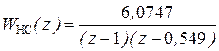 .
.
В общем виде 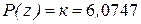 ,
, 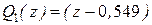 ,
, 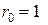
По табл.2 находим, что для 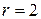 , для компенсированной ДПФ
, для компенсированной ДПФ
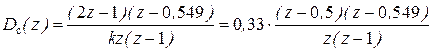 ,
,
а ДПФ корректирующего фильтра 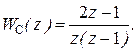
Рассмотрим случай цифрового регулирования скорости ДПТ, когда в контуре регулирования тока используется релейный широтно-импульсный регулятор, В таком случае контур тока можно считать практически безинерционным с коэффициентом передачи 1/КДТ. ПФ неизменяемой части контура скорости согласно приведенной на рис.6 структурной схемы и с учетом запаздывания вычислений алгоритма в микро-ЭВМ равна:
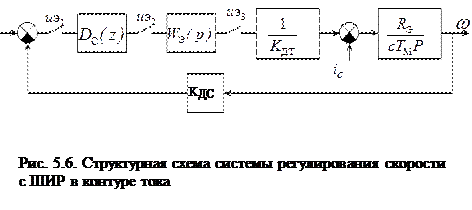 |
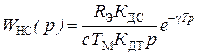 .
.
С учетом экстраполятора нулевого порядка определим ДПФ неизменяемой части контура скорости с помощью модифицированного z – преобразования
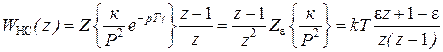 ,
,
где 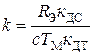 .
.
Полагая 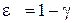 , найдем ДПФ неизменяемой части САР скорости
, найдем ДПФ неизменяемой части САР скорости
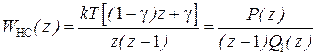 , (5.36)
, (5.36)
где 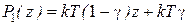 ,
, 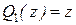 ,
, 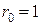
Выполним синтез регулятора скорости для случая, когда порядок астатизма системы 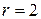 . Порядок полиномов
. Порядок полиномов 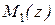 и
и 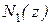 должен удовлетворять условиям:
должен удовлетворять условиям:
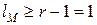 ,
, 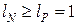 ,
, 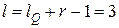 ,
,
следовательно, ищем 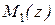 в виде
в виде 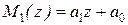 , а
, а 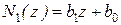 из равенства
из равенства
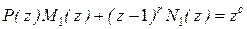 .
.
Обозначим 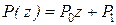 , где
, где 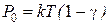 ,
, 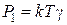 , и получаем равенство следующего вида
, и получаем равенство следующего вида
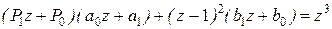
Раскрывая скобки и приравнивая коэффициенты в левой и правой частях равенства при одинаковых степенях z, составляем систему уравнений
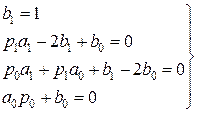
Решая уравнения совместно, находим
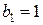 ,
, 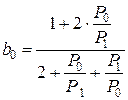 ,
, 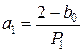 ,
, 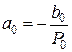 .
.
ДПФ регулятора скорости 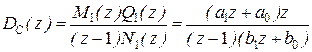 , а ДПФ замкнутого контура скорости
, а ДПФ замкнутого контура скорости 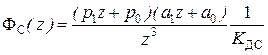 .
.
Так как в большинстве случаев переходный процесс в cинтезированной системе отличается большим перерегулированием, рассмотрим случай введения ''коэффициента жёсткости'', для этого представим исходное для нахождения M1(z) и N1(z) равенство в виде 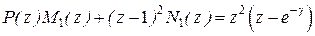 , или
, или
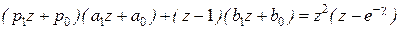 .
.
Приравнивая коэффициенты при одинаковых степенях z в левой и правой частях равенства, находим 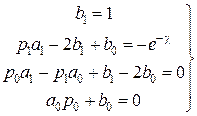 .
.
Решая совместно, получим, b1 =1
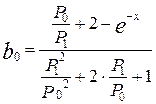 ,
, 
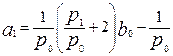 ,
, 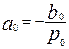 .
.
 Пример расчета 10. Используя данные примера 2, рассчитаем регулятор скорости, если в контуре тока применен релейный ШИР. Примем при расчёте
Пример расчета 10. Используя данные примера 2, рассчитаем регулятор скорости, если в контуре тока применен релейный ШИР. Примем при расчёте 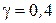 .
.
|
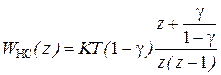 ,
,
где 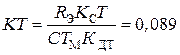 ;
; 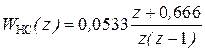 .
.
Следовательно, 
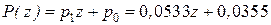 .
.
Находим коэффициенты полиномов M1(z) и N1(z), входящих в ДПФ регулятора скорости 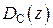 : b1=1, b0=0,56, a1=26,736, a0=15,6. ДПФ регулятора скорости в этом случае равна
: b1=1, b0=0,56, a1=26,736, a0=15,6. ДПФ регулятора скорости в этом случае равна 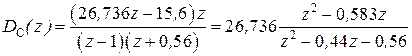 , ДПФ замкнутой системы
, ДПФ замкнутой системы 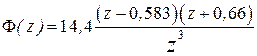 .
.
Дата добавления: 2021-01-11; просмотров: 647;











