Синтез компенсационного регулятора тока

ДЧX неизменяемой части контура регулирования тока с учётом запаздывания имеет вид

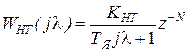. (5.47)

Стандартную форму желаемой ДЧX задаём в виде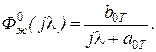

С учётом необходимости получения астатизма первого порядка в регуляторе тока примем .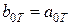

Контур тока является наиболее быстродействующим из всех контуров регулирования, поэтому для синтеза регулятора тока будем использовать табличные преобразования ДЧX в ДПФ [1].

По таблицам z– преобразования найдём ДПФ

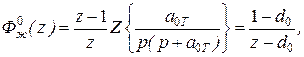(5.48)

где 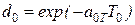. Определим для N=1 выражение

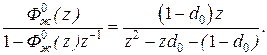(5.49)

Обозначим B₁=(1-d₀), B₀=0, A₃=1, A₂=-d₀, A₁=0, A₀= - (1-d₀).

Определим это же выражение для N=2

.

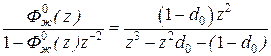Обозначим: B₂=(1– d₀), B₁=0, B₀=0, A₃=1, A₂= – d₀, A₁=0, A₀= – (1–d₀).

По таблицам z-преобразования найдём ДПФ неизменяемой части контура регулирования тока

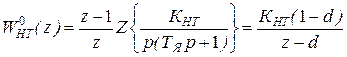, где .

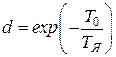Введём запись ДПФ неизменяемой части контура в общем виде

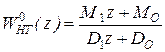, (5.50)

где , , , .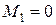

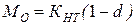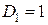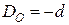ДПФ регулятора тока в общем виде представляется выражением

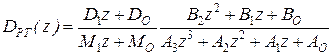(5.51)

Подставляя выше найденные коэффициенты A_i и B_i, определим ДПФ регулятора тока:

для N=1 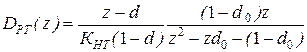, (5.52)

для N=2 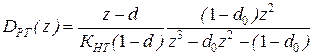. (5.53)

Коэффициенты стандартной формы 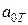и 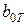рекомендуется принимать из условия 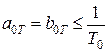, что обеспечивает частоту среза контура тока .

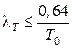По сравнению с обычным цифровым ПИ – регулятором тока компенсационный регулятор обеспечивает желаемую форму переходного процесса (апериодическую) при сохранении или даже некотором увеличении полосы пропускания контура.