Уравнение движения агрегата

Машинно-тракторный агрегат (МТА) является динамической системой твердых тел с жесткими и упругими связями между ними. Движение агрегата происходит при определенном соотношении сил, действующих на агрегат. Прирассмотрении общей динамики МТА все силы, действующие на агрегат, можно разделить на две группы:

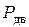· ¾ сила, вызывающая движение агрегата;

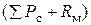· ¾ силы сопротивления движению трактора и рабочей машины.
Поэтому под уравнением движения агрегата понимают зависимость

между силами, действующими на агрегат, и скоростью его движения. Такое уравнение может быть получено на основании закона о сохранении кинетической энергии, из которого следует, что изменение кинетической энергии равно работе сил, действующих на агрегат при движении.

Элементарная работа dA сил пути dS:

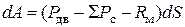, (2.1)

где 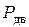¾внешняя сила, приложенная к трактору и вызывающая его движе-

ние (движущая сила);

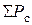¾ силы сопротивления движению трактора;

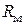¾ тяговое сопротивление машины.

Кинетическая энергия агрегата

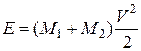, (2.2)

где 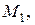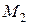¾ соответственно масса трактора и рабочей машины, приве-

денные к осям ведущих колес трактора;

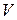¾ скорость движения агрегата.

Приращение кинетической энергии агрегата 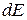вызывает увеличение работы 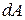. Величина 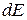определяется дифференцированием уравнения (2.2) по скорости движения:

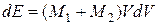. (2.3)

Приравняв уравнения (2.1) и (2.3), получим

.

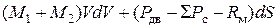Учитывая, что скорость движения V есть первая производная от пути 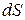по времени 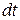, т.е. 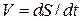,и подставляя в уравнение, получим:

.

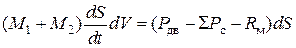После преобразования имеем:

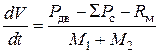, (2.4)

что является уравнением движения агрегата с точки зрения общей динамики МТА.

Левая дифференциальная часть уравнения (2.4) представляет собой ускорение поступательно движущегося агрегата, 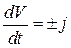. Знакопеременное значение ускорения соответствует ускоренному (знак «+») или замедленному (знак «-») движению. Знак и значение ускорения зависят от соотношения действующих сил и величины приведенных масс агрегата.

Если агрегат движется с ускорением или замедлением, то такой режим принято называть неустановившимся. В этом случае уравнение движения принимает следующий вид:

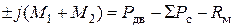. (2.5)

Произведение 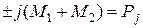¾ сила инерции движущегося агрегата, откуда

.

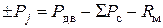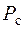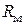Из уравнения (2.5) следует, что величина приведенных масс оказывает существенное влияние на динамику движения агрегата при неустановившемся движении. Наличие силы инерции приводит к саморегулированию баланса между движущей силой Р_дви постоянно изменяющимися силами сопротивления и .При ускоренном движении агрегата сила инерции 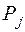¾направлена против движения и становится силой сопротивления, при замедлении сила 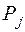направлена по ходу движения и является движущей силой. Следовательно, чем больше величина приведенных масс агрегата, тем устойчивее его движение.

Однако саморегулирование вследствие вышеназванных причин возможно лишь пока запаса кинетической энергии агрегата при переменной скорости его движения достаточно для преодоления временно возросшего сопротивления движению.

При дальнейшем увеличении сопротивления оно будет преодолеваться за счет запаса крутящего момента двигателя (работа корректора регулятора) или перехода на пониженную передачу. Это в обоих случаях приводит к увеличению движущей силы .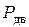

При движении агрегата с постоянной скоростью 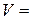const ускорение 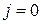, и уравнение движения принимает следующий вид:

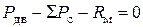. (2.7)

Такой режим движения называется установившимся, а уравнение (2.7) ¾ уравнением установившегося движения агрегата.