При синтезе технологического маршрута

На основе графа может быть создана формализованная модель геометрической структуры детали. Для этого необходимо, чтобы исходная геометрическая информация о детали была полностью описана в цифровой форме. Следовательно, задача построения формализованной модели геометрической струк­туры детали сводится к распознаванию ее размерных связей в таблице кодированных сведений и построению матрицы смежности соответст­вующего графа.

При неавтоматизированном проектировании для распознавания размерных связей технолог визуально анализирует параметры точно­сти, выявляет необходимые связи между ними, исходя из конкретных условий производит анализ размерных цепей и их пересчет и назначает технологический процесс изготовления детали.

В условиях автоматизированного проектирования процесс построе­ния формализованной модели структуры детали производится путем анализа информации, содержащейся в таблице кодированных сведе­ний, заполненной согласно принятой для данной САПР ТП системе кодирования (язык описания детали). Для решения рассматриваемой задачи ТКС должна содержать определенный набор реквизитов (сведе­ний), необходимых для построения формализованной модели.

К рек­визитам, описывающим положение отдельной поверхности в общей конструкции детали, относятся:

- номер элемента НЭ,

- код элемента КЭ,

- номер базы НБ,

- размеры (х, у, z),

- верхнее отклонение размера ВО,

- нижнее отклонение размера НО.

В результате выборки из ТКС формируется таблица, являющаяся исходной для алгоритма формирования графа размерных связей дета­ли. Она представляет двухмерный массив М (т, п),где т = 6 – число реквизитов, описывающих положение i-и поверхности; п – количе­ство поверхностей детали.

В качестве примера рассмотрим построение графа размерных свя­зей в координатном направлении z для детали типа «вал» (рис. 6.5) составлена таблицу 6.1 выборки сведений из ТКС.

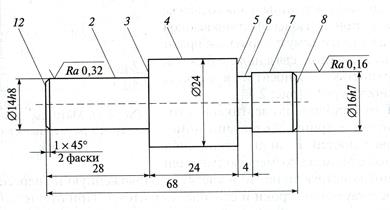
Рис. 6.5 Эскиз детали типа «Вал»

Чтобы построить граф размерных связей детали в автоматизирован­ном режиме, необходимо сформировать матрицу смежности. Для ее по­строения следует из множества поверхностей детали выделить базовую поверхность, которую принимает пользователь в качестве начальной вершины графа. Данная задача является достаточно важной, так как от нее зависит структура формализованной модели. При этом необхо­димо учитывать правила построения технологических процессов. Одно из таких правил определяет необходимость подготовки в первую оче­редь технологических установочных баз. Поэтому в качестве начальной вершины графа размерных связей используются поверхности, служа­щие технологическими установочными базами и обрабатываемые на первой операции. Это условие при автоматизированном проектирова­нии должно быть обязательно проверено.

Алгоритм формирования графа размерных связей строится следующим образом. Для принятой базовой поверхности (начальной вершины графа) определяют висячие вершины первого дерева графа. С этой целью из сформированной таблицы (по третьему столбцу) выбирают номера элементов, связанные с базовой поверхностью, и заносят их в матрицу смежности.

Таблица 6.1

Выборка сведений из ТКС

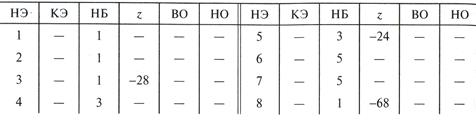
В этой таблице по вертикали и по горизонтали матрицы обозначены номера поверхностей. Если две какие-либо поверхности имеют размерную связь или связаны конструктивно, то в клетку, расположенную на пересечении соответствующей строки и столбца, ставят 1. При отсутствии размерной связи в клетку ставится нуль, который для упрощения таблицы может быть опущен.

В рассматриваемом примере в качестве базовой принята поверх­ность с номером 1. С этой поверхности начинается формирование матрицы смежности (рис. 6.6).

Рис.6.6 Матрица смежности графа размерных связей по оси z

Граф размерных связей детали можно рассматривать состоящим из отдельных деревьев (кустов), каждый из которых имеет одну начальную (базовую) вершину и несколько (в крайнем случае, одну) висящих вер­шин. При формировании матрицы смежности происходит выделение деревьев графа.

После построения первого дерева графа производится формирова­ние его последующих деревьев. Для этого необходимо проверить, не является ли поверхность, соответствующая выбранной висящей вер­шине, базовой для других поверхностей. Если да, то повторяется по­следовательность выбора элементов с висящими вершинами по отно­шению к этой базовой поверхности.

После заполнения матрицы смежности графа может быть сформирован граф размерных связей по оси z (рис. 6.7).

Рис. 6.7 Граф размерных связей

детали типа «Вал»

В памяти ЭВМ граф размерных связей детали описывается массивом (ГРАФ), который используется в дальнейшем как математическая модель при выборе технологических баз и проектировании технологических маршрутов.

Граф размерных связей детали можно рассматривать как формали­зованную модель структуры детали, определяющую последовательность обработки технологических баз. В этой модели одна из двух вершин, принадлежащих какому-либо ребру, всегда служит базой для другой. При этом под термином база подразумевается совокупность поверхно­стей, линий или точек детали, относительно которых ориентируются другие поверхности детали.

Известно, что для обработки ответственных поверхностей детали необходимо предварительно обработать соответствующую ей (по раз­мерным связям) базовую поверхность до требуемой степени точности и шероховатости. При этом часто конструкторские базы не могут быть использованы в качестве технологических, поэтому приходится опре­делять дополнительные или вводить искусственные базы. Например, для деталей типа «тела вращения», у которых длина превышает диаметр, в качестве искусственных опорных баз используются центровые отвер­стия, поэтому для них формируется граф размерных связей с искусст­венными опорными базами. Для детали типа «вал» такой граф представлен на рис. 6.8.

Рис. 6.8 Граф размерных связей с опорными

базами для детали типа «Вал» (массив МГОБ)

В граф размерных связей детали введены две искусственные опорные базы (80 и 10) как третий и четвертый элементы массива, получившего название массива графа размерных связей с опорными базами (МГОБ). При проектировании технологических процессов в САПР ТП широко используются наработанные типовые решения различных подзадач для типовых элементов ТП, например, типовые планы обработки. Полный подход позволяет наиболее рационально сочетать объективные факторы проектирования технологических процессов (размерные характеристики деталей) с типовыми решениями, характеризующими специфику конкрет­ного предприятия. Поэтому синтез технологического маршрута из­готовления детали производится на основе планов обработки элемен­тарных и типовых поверхностей.

Планы обработки на отдельные поверхности, обеспечивающие по­лучение требуемой точности и качества, разрабатывают расчетным либо статистическим методом, и на первом этапе происходит формирование плана обработки. Выбор плана обработки производится на основе ана­лиза таблиц соответствий,представляющих собой одну из форм записи соответствия множества типовых решений множеству условий их суще­ствования.

В качестве условий, определяющих выбор того или иного плана обработки W_i,принимаются вид (код) обрабатываемого элемента по­верхности КЭ, вид термообработки ТО, шероховатость поверхности, квалитет точности КТ, отклонения взаимного расположения ∆, диаметр обработки D, расположение отверстий ОТ, вид отверстия ВО и др. В зависимости от этих условий из таблицы типовых планов обработки поверхностей (табл. 6.2) выбирают планы W_i на каждую обрабатываемую поверхность и формируют таблицу планов обработки поверхностей детали.

Таблица 6.2

Планы обработки поверхностей (массив ПЛОБ)

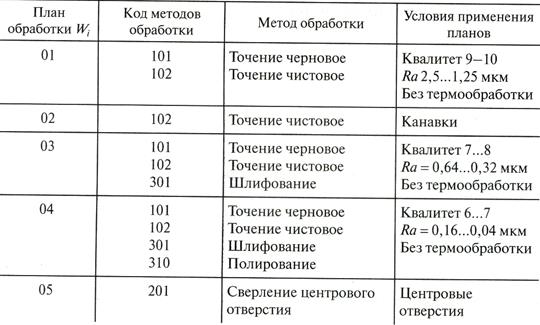
Для детали типа «вал» сформирована таблица 6.3 – массив МПО W.

Таблица 6.3

Планы обработки поверхностей детали типа Вал (массив МПО W)

Следующим этапом синтеза технологического маршрута является объединение одноименных технологических методов обработки, име­ющих общий код методов обработки (КМО) и принадлежащих разным вершинам вторичного графа (рис. 6.9). Для этого массив вторичного графа с учетом массива ПЛОБ поверхностей разбивается на операцион­ные подграфы, вершины которых содержат одноименные методы обра­ботки и соединены между собой ребрами, принадлежащими вторич­ному графу.

На заключительном этапе синтеза технологического маршрута на­значается последовательность выполнения операций, т.е. задача сво­дится к упорядочиванию операционных подграфов. С этой целью вы­полняется проверка технологических операций на совместимость, т.е. возможность предшествования операций друг другу в типовых схемах построения маршрутной технологии.

Для проверки операций на совместимость служит таблица, в ко­торой операции записаны в порядке их возможного выполнения. Эта таблица строится разработчиками САПР ТП на основе положений тех­нологии машиностроения, согласно которым вначале подготавливают технологические базы, затем выполняют черновые, чистовые и отде­лочные операции.

В результате проектирования сформирован технологический марш­рут механической обработки заготовки детали «вал» (табл. 6.4).

Таблица 6.4

Технологический маршрут изготовления детали типа «Вал»

Полученный в результате синтеза технологический маршрут может уточняться в дальнейшем на стадии проектирования операционной технологии с учетом технических ограничений, обусловленных наборами типоразмеров оборудования, применяемого в цехах завода для выполнения указанной операции, универсальных, групповых и специализированных установочно-зажимных приспособлений, используемых на каждом тире станков, и другими условиями.

Рис. 6.9 Вторичный граф размерных связей

детали типа «Вал»

Вопросы для самопроверки

1. Какова иерархическая структура технологического процесса как объекта автоматизированного проектирования?

2. Какая исходная информация необходима для автоматизированного про­ектирования технологических процессов?

3. В чем сущность принципа системного подхода при компьютерном проек­тировании?

4. Какие технические ограничения существуют при проектировании струк­туры технологических операций?

5. В чем сущность формализации этапов проектирования технологических процессов?

6. Как и зачем используют математическое моделирование в САПР ТП?

7. Какие этапы решения задач методом математического моделирования?

8. В чем сущность метода прямого проектирования, используемого в САПР ТП?

9. В чем сущность метода анализа и метода синтеза, используемых в САПР ТП?

10. В чем сущность принципов совместимости, типизации и развития в совре­менных САПР ТП?

ЗАДАЧИ ОПТИМИЗАЦИИ

В самом общем случае решить оптимизационную задачу – значит найти наилучшее решение среди возможных вариантов решения.

Если оптимизация связана с расчетом оптимальных значений параметров при заданной структуре объекта, то она называется параметрической. Задача выбора оптимальной структуры является структурной оптимизацией.

Решение любой оптимизационной задачи основано на построении математической модели исследуемого объекта и проведении вычислительного эксперимента. Нахождение оптимальных значений параметров – это один из этапов вычислительного эксперимента, позволяющий выработать управляющее воздействие на объект исследования.

Теория оптимизации представляет собой совокупность фундаментальных математических результатов и численных методов, позволяющих избежать полного перебора всех решений.

Методы оптимизации – это методы построения алгоритмов нахождения оптимального (минимального или максимального) значения некоторой функции.

Содержательная и формализованная постановка задачи

Решение оптимизационных задач (процесс оптимизации) лежит в основе всей инженерной деятельности.

Эффективность метода оптимизации связана с одной стороны с умелым использованием основных результатов таких математических дисциплин, как:

· математический анализ;

· линейная алгебра;

· математическая логика и теория алгоритмов;

· функциональный анализ;

· дифференциальное исчисление.

С другой стороны, в инженерной практике размер оптимизационных задач достаточно велик, следовательно, велики и затраты времени реализации алгоритмов. Поэтому оптимизационные задачи ориентированы в основном на реализацию на ЭВМ.

Ценность теории оптимизации состоит в её универсальности по отношению к различным классам задач.

Оптимизационная задача может быть частью задачи решаемой:

· в математической экономике: решение больших макроэкономических моделей, моделей предпринимательства и т. д.;

· автоматике: оптимальное управление, робототехника, фильтрация, управление производством;

· технике: оптимальное планирование информационных и компьютерных сетей, оптимизация структур и параметров технических систем;

· численном анализе: аппроксимация, регрессия, решение линейных и нелинейных систем управления и т. д.

Важнейшим элементом во всех этих задачах является формализованная (математическая) постановка задачи. При этом задачи различаются содержательной стороной. Рассмотрим ряд содержательных и формализованных задач оптимизации.

Важнейшим моментом теории оптимизации является переход от содержательной постановки задачи к формализованной, то есть математической. При этом, решение задачи оптимизации – это всего лишь один этап в процессе формирования оптимального проекта для эффективного функционирования системы.

Переход от содержательной к формализованной постановке задачи оптимизации включает ряд этапов, важнейшими из которых являются следующие.

1. Установка границы объекта оптимизации

Границы объекта (системы) задаются пределами, отделяющими объект от внешней среды. Так, в примере I мы не рассматривали процесс получения градуировочной таблицы. Однако при установлении границ должны быть уверены, что декомпозиция задачи не приведет к излишнему упрощению реального объекта.

2. Построение математической модели системы

Структура модели включает основные уравнения материальных и энергетических балансов и уравнения, описывающие физические процессы в системе. Эти уравнения обычно дополняются неравенствами, которые определяют область допустимых значений независимых переменных. Область допустимых значений определяет границы изменения характеристик объекта. Процесс построения математической модели – один из самых сложных этапов.

3. Выбор критерия оптимизации

Зависит от решаемой задачи и может иметь экономический, точностный или надежностный характер. Независимо от характера критерия наилучшему решению задачи оптимизации всегда соответствуют минимум или максимум его значения.

Чаще всего критерий оптимальности носит экономическую оценку (производительность, себестоимость продукции, прибыль, рентабельность и др.). Но если объект оптимизации является частью технологического процесса, то не всегда целесообразно выделять прямой экономический показатель, который бы полностью характеризовал эффективность работы рассматриваемого объекта. В таких случаях критерием оптимальности может служить технологическая характеристика, косвенно оценивающая экономичность работы устройства (технологические параметры и другие показатели качества продукции).

Основная задача при выборе критерия оптимизации – декомпозиция противоречивых целевых установок.

Например:

минимум затрат (вложений при проектировании);

минимум потребления энергии при эксплуатации;

максимум надежности.

В таком случае чаще всего выделяют главный критерий, а остальные – вводятся в ограничение задачи оптимизирования. Подобные задачи относятся к классу задач векторной оптимизации.

4. Формирование целевой функции

На основании выбранного критерия оптимизации необходимо составить целевую функцию (функцию качества), представляющую собой математическую зависимость критерия оптимальности от параметров, влияющих на ее значение. Вид целевой функции определяется конкретной задачей оптимизации.

Таким образом, задача оптимизации сводится к нахождению экстремума целевой функции.

5. Построение оптимизационного алгоритма и решение экстремальной задачи

Этот этап, собственно, и представляет выбор или разработку алгоритма решения инженерной задачи с использованием средств вычислительной техники.

Классификация задач оптимизации

В зависимости от вида целевой функции и соотношения ограничений выделяют различные задачи оптимизации.

Существует несколько признаков классификации.

Основные критерии следующие:

1. По типу параметров задачи оптимизации.

Различают непрерывные задачи оптимизации (continues optimization), дискретные (discrete) и целочисленные (integer optimization).

2. По критерию размерности допустимого множества параметров D.

Задачи оптимизации по этому критерию делятся на задачи одномерной

и многомерной оптимизации.

3. По критерию наличия или отсутствия ограничений на допустимое множество D.

Различают задачи условной (constrained) и безусловной (unconstrained) оптимизации. Этот признак классификации имеет место как для одномерных, так и для многомерных задач оптимизации.

4. По характеру ограничений. Различают детерминированную оптимизацию и стохастическую. Если множество допустимых значений включает случайные компоненты, то имеет место стохастическое программирование. При этом стохастическая оптимизация может относиться и к дискретной задаче.

5. По виду целевой функции и виду ограничений. Различают линейное и нелинейное программирование.

Задача линейного программирования содержит линейную целевую функцию, ограничения в задаче также линейны.

При нарушении линейности целевой функции или ограничений имеет место нелинейная задача оптимизации.

Целевая функция – линейна, ограничения тоже линейны.

Наиболее известные классические задачи линейного программирования: транспортная задача, задача о диете и другие.

Задача целочисленного программирования

В задачах целочисленного программирования компоненты вектора {x} принимают только целые значения. Известны классические задачи целочисленного программирования: задача о коммивояжере, раскраски графов, теории расписания.